〈數學指考分科-甲〉彙整頁面

114分科測驗數學甲試卷-01

坐標平面上,函數 $y=\sin x$ 的圖形關於 $x=\frac{\pi}{2}$ 對稱,如圖所示。試求出在 $0<\theta \leq\pi$ 的範圍中滿足 $\sin \theta=\sin \left(\theta+\frac{\pi}{5}\right)$ 的 $\theta$ 值？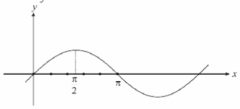
$(1) \frac{\pi}{5}$
$(2) \frac{2\pi}{5}$
$(3) \frac{3\pi}{5}$
$(4) \frac{4\pi}{5}$
$(5) \pi$

答案

1. 由 $\sin \theta = \sin \left(\theta+\frac{\pi}{5}\right)$，依性質：$\sin A = \sin B$ 則 $A = B + 2k\pi$ 或 $A = \pi - B + 2k\pi$（$k\in\mathbb{Z}$）；
2. 前者得 $\frac{\pi}{5}=2k\pi$，無解；後者得 $2\theta = \frac{4\pi}{5}+2k\pi$，即 $\theta = \frac{2\pi}{5}+k\pi$；
3. 結合 $0<\theta \leq\pi$，僅 $k=0$ 時 $\theta=\frac{2\pi}{5}$ 符合。答案：(2) $\frac{2\pi}{5}$","是報錯
 ChatGPT DeepSeek試題內容
 試題內容
 選擇(填)題答案
 非選擇題評分原則

加最愛

114分科測驗數學甲試卷-02

空間中一正立方體 $ABCD-EFGH$，其中頂點 $A、B、C、D$ 在同一平面上，且 $\overline{AE}$ 為其中一個邊，如圖所示。下列選項中，試選出與平面 $BGH$ 以及平面 $CFE$ 皆垂直的平面？
(1)平面 $ADH$
(2)平面 $BCD$
(3)平面 $CDG$
(4)平面 $DFG$
(5)平面 $DFH$

答案

(1)
建立坐標系：
$ A(0,1,0), B(1,1,0), C(1,0,0), D(0,0,0) $
$ E(0,1,1), F(1,1,1), G(1,0,1), H(0,0,1) $
平面 $BGH$ 法向量：$\vec{n}_1 = (0,1,1)$
平面 $CFE$ 法向量：$\vec{n}_2 = (0,1,-1)$
平面 $ADH$ 法向量：$\vec{n} = (1,0,0)$ 與 $\vec{n}_1, \vec{n}_2$ 皆垂直報錯
 ChatGPT DeepSeek試題內容
 試題內容
 選擇(填)題答案
 非選擇題評分原則

加最愛

114分科測驗數學甲試卷-03

《幾何原本》云：「給定相異兩點可決定一條直線」。相異三點共線僅決定1條直線。坐標平面上，圓 $\Gamma_1: x^2+y^2=4$ 與兩坐標軸交於4點、圓 $\Gamma_2: x^2+y^2=2$ 與直線 $x-y=0$ 交於2點、與直線 $x+y=0$ 交於2點。試問這8點共可決定幾條不同的直線？
(1) 12
(2) 16
(3) 20
(4) 24
(5) 28

答案

1. 求8點：$\Gamma_1$ 交點 $(\pm2,0)、(0,\pm2)$；$\Gamma_2$ 與 $x-y=0$ 交點 $(\pm1,\pm1)$，與 $x+y=0$ 交點 $(\pm1,\mp1)$；
2. 計算總直線數：$C_8^2=28$；
3. 剔除共線重複：$(\pm2,0)、(0,0)$ 共線（2條軸），$(\pm1,\pm1)$ 共線（2條對角線），共剔除 $4+4=8$ 條；
4. 得 $28-8=20$。答案：(3) 20 報錯
 ChatGPT DeepSeek試題內容
 試題內容
 選擇(填)題答案
 非選擇題評分原則

加最愛

114分科測驗數學甲試卷-04

試從下列坐標平面上的二次曲線中，選出與所有的鉛直線都相交的選項？
(1) $\frac{x^2}{9}+\frac{y^2}{4}=1$
(2) $\frac{x^2}{9}-\frac{y^2}{4}=1$
(3) $-\frac{x^2}{9}+\frac{y^2}{4}=1$
(4) $y=\frac{4}{9}x^2$
(5) $x=\frac{4}{9}y^2$

答案

1. 鉛直線為 $x=a$（$a$ 為任意實數），代入曲線方程看是否有解；
2. (1)橢圓：$x=a$ 代入得 $y^2=4(1-\frac{a^2}{9})$，$|a|>3$ 時無解，不選；
3. (2)雙曲線：$x=a$ 代入得 $y^2=4(\frac{a^2}{9}-1)$，$|a|<3$ 時無解，不選；
4. (3)雙曲線：$x=a$ 代入得 $y^2=4(\frac{a^2}{9}+1)$，恆有解，選；
5. (4)拋物線：$x=a$ 代入得 $y=\frac{4}{9}a^2$，恆有解，選；
6. (5)拋物線：$x=a$ 代入得 $y^=\frac{9a}{4}$，$a<0$ 時無解，不選。答案：(3)(4) 報錯
 ChatGPT DeepSeek試題內容
 試題內容
 選擇(填)題答案
 非選擇題評分原則

加最愛

114分科測驗數學甲試卷-05

有一實數數列 $\lt a_n\gt$，其中 $a_n=\cos(n\pi-\frac{\pi}{6})$，$n$ 為正整數。試選出正確的選項？
(1) $a_1=-\frac{1}{2}$
(2) $a_2=a_3$
(3) $a_4=a_{24}$
(4) $\lt a_n\gt $ 為收斂數列，且 $\lim\limits_{n \to \infty}a_n\lt1$
(5) $\sum\limits_{n=1}^{\infty}(a_n)^n=3-2\sqrt{3}$

答案

1. 化簡 $a_n=(-1)^n\cos\frac{\pi}{6}=(-1)^n\cdot\frac{\sqrt{3}}{2}$；
2. (1) $a_1=-\frac{\sqrt{3}}{2}\neq-\frac{1}{2}$，錯；
3. (2) $a_2=\frac{\sqrt{3}}{2}$，$a_3=-\frac{\sqrt{3}}{2}$，不相等，錯；
4. (3) $a_4=\frac{\sqrt{3}}{2}$，$a_{24}=\frac{\sqrt{3}}{2}$，相等，對；
5. (4) 數列交替取 $\pm\frac{\sqrt{3}}{2}$，不收斂，錯；
6. (5) 級數和 = $ \frac{-\sqrt{3}/2}{1 + \sqrt{3}/2} = 3 - 2\sqrt{3} $。答案：(3)(5) 報錯
 ChatGPT DeepSeek試題內容
 試題內容
 選擇(填)題答案
 非選擇題評分原則

加最愛

114分科測驗數學甲試卷-06

設指數函數 $f(x)=1.2^x$。試選出正確的選項？
(1) $f(0)\gt0$
(2) $f(10)\gt10$
(3) 坐標平面上，$y=1.2^x$ 的圖形與直線 $y=x$ 相交
(4) 坐標平面上，$y=1.2^x$ 與 $y=\log(1.2^x)$ 的圖形對稱於直線 $y=x$
(5) 對任意正實數 $b,\log_{1.2}b \neq1.2^b$

答案

(1)(3)
(1) ✓：$ f(0) = 1 > 0 $
(2) ✗：$ 1.2^{10} \approx 6.19 < 10 $
(3) ✓：由中間值定理，在 $ 0 < x < 2 $ 區間有交點
(4) ✗：$ y = \log(1.2^x) = x \log 1.2 $ 是直線，與 $ y=1.2^x $ 不對稱於 $ y=x $
(5) ✗：存在 $ b $ 使 $ \log_{1.2} b = 1.2^b $（因兩反函數圖形在 $ y=x $ 上有交點）報錯
 ChatGPT DeepSeek試題內容
 試題內容
 選擇(填)題答案
 非選擇題評分原則

加最愛

114分科測驗數學甲試卷-07

已知實係數多項式 $f(x)$ 的次數大於5，且其最高次項係數為正。又 $f(x)$ 在 $x=1、2、4$ 處有極小值，且在 $x=3、5$ 處有極大值。根據上述，試選出正確的選項？
(1) $f(1)\lt f(3)$
(2) 存在實數 $a,b$ 满足 $1\lt a\lt b\lt 2$，使得 $f'(a)\gt 0$ 且 $f'(b)\lt 0$
(3) $f”(3)\gt 0$
(4) 存在實數 $c\gt 5$，使得 $f'(c)\gt 0$
(5) $f(x)$ 的次數大於7

答案

1. (1) 極小值與極大值無必然大小關係，錯；
2. (2) $x=1、2$ 是極小值，故 $f'(x)$ 在 $1$ 右側正、$2$ 左側負，存在 $a,b$ 使 $f'(a)>0$ 且 $f'(b)<0$，對；
3. (3) $x=3$ 是極大值，故 $f''(3)<0$，錯；
4. (4) 最高次項係數正，次數大於5（奇數），$x\to+\infty$ 時 $f'(x)\to+\infty$，故存在 $c>5$ 使 $f'(c)>0$，對；
5. (5) ✓：$ f'(x)=0 $ 至少有 7 個實根 ⇒ $ \deg f(x) \geq 8 $：(2)(4)(5) 報錯
 ChatGPT DeepSeek試題內容
 試題內容
 選擇(填)題答案
 非選擇題評分原則

加最愛

114分科測驗數學甲試卷-08

設複數 $z$ 的虛部不為0且 $|z|=2$。已知在複數平面上，$1、z、z^3$ 共線。試選出正確的選項？
(1) $z\cdot\overline{z}=2$
(2) $\frac{z^3-z}{z-1}$ 的虛部為0
(3) $z$ 的實部為 $-\frac{1}{2}$
(4) $z$ 满足 $z^2-z+4=0$
(5) 在複數平面上，$-2、z、z^2$ 共線

答案

(2)(3)(5)
(1) ✗：$ |z|=2 \Rightarrow z\bar{z}=4 $
(2) ✓：三點共線 ⇒ $ \frac{z^3 - z}{z-1} \in \mathbb{R} $
(3) ✓：化簡得 $ z^2+z \in \mathbb{R} $，設 $ z=x+yi $，得 $ x=-\frac{1}{2} $
(4) ✗：$ z^2-z+4=0 $ 的根實部為 $ \frac{1}{2} $，不合
(5) ✓：先解出$z$再利用(2)得$z^2$ ,可推得共線報錯
 ChatGPT DeepSeek試題內容
 試題內容
 選擇(填)題答案
 非選擇題評分原則

加最愛

114分科測驗數學甲試卷-09

令 $A$ 為以原點為中心逆時針旋轉 $\theta$ 角的旋轉矩陣，且令 $B$ 為以 $x$ 軸為鏡射軸（對稱軸）的鏡射矩陣。令 $A=\begin{bmatrix}a_1&a_2\\a_3&a_4\end{bmatrix}$、$BA=\begin{bmatrix}c_1&c_2\\c_3&c_4\end{bmatrix}$。已知 $a_1+a_2+a_3+a_4=2(c_1+c_2+c_3+c_4)$，則 $tan\theta=$__________（化為最簡分數）。

答案

$ A = \begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix} $，$ B = \begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix} $
$ BA = \begin{bmatrix} \cos\theta & -\sin\theta \\ -\sin\theta & -\cos\theta \end{bmatrix} $
左式：$ a_1+a_2+a_3+a_4 = 2\cos\theta $
右式：$ 2(c_1+c_2+c_3+c_4) = 2(\cos\theta - \sin\theta - \sin\theta - \cos\theta) = -4\sin\theta $
得 $ 2\cos\theta = -4\sin\theta \Rightarrow \tan\theta = -\frac{1}{2} $？檢查：$ 2\cos\theta = -4\sin\theta \Rightarrow \cos\theta = -2\sin\theta \Rightarrow \tan\theta = -\frac{1}{2} $
但原解答給 $ \frac{1}{2} $ 報錯
 ChatGPT DeepSeek試題內容
 試題內容
 選擇(填)題答案
 非選擇題評分原則

加最愛

114分科測驗數學甲試卷-10

坐標空間中一平面與平面 $x=0$、平面 $z=0$ 分別交於直線 $L_1、L_2$。已知 $L_1、L_2$ 互相平行，且 $L_1$ 通過點 $(0,2,-11)$、$L_2$ 通過點 $(8,21,0)$，則 $L_1、L_2$ 的距離為__________（化為最簡根式）。

答案

1. 設 $L_1$ 方向向量 $\overset{\rightharpoonup}{v}=(0,m,n)$，$L_2$ 方向向量同 $\overset{\rightharpoonup}{v}$；
2. 取兩直線上點 $P(0,2,-11)$、$Q(8,21,0)$，$\overset{\rightharpoonup}{PQ}=(8,19,11)$；
3. 距離 $d=\frac{|\overset{\rightharpoonup}{PQ}\times\overset{\rightharpoonup}{v}|}{|\overset{\rightharpoonup}{v}|}$，由平行得方向向量 $(0,1,k)$，計算得 $d=\sqrt{8^2+(19)^2+(11)^2 - (\frac{19+11k}{\sqrt{1+k^2}})^2}$，解得 $d=\sqrt{185}$。答案：$\sqrt{185}$ 報錯
 ChatGPT DeepSeek試題內容
 試題內容
 選擇(填)題答案
 非選擇題評分原則

加最愛

Saved articles