假設兩數列\(\lt a_{n}\gt\)、\(\lt b_{n}\gt\) ,對所有正整數\(n\)都滿足\(b_{n}+\frac{4n – 1}{n}\lt a_{n}\lt 3b_{n}\) 。已知\(\lim_{n\rightarrow\infty}a_{n}=6\) ,試選出正確的選項。
(1)\(b_{n}\lt6-\frac{4n – 1}{n}\)(2)\(b_{n}\gt\frac{4n – 1}{2n}\)(3)數列\(\lt b_{n}\gt\)有可能發散
(4)\(a_{10000}\lt6.1\)(5)\(a_{10000}\gt5.9\)
數學指考分科-甲
111分科數學甲試題-09
大吉百貨春節期間準備許多紅包讓顧客抽籤得紅包,並宣稱活動會一直持續到送 出所有的紅包。抽籤的籤筒內有5支籤、其中只有1支籤有標示「大吉」,且每支籤被抽中的機會均等。每位顧客從籤筒中抽取一支籤記錄後,將籤放回籤筒再抽下一回,最多抽取3回。當抽取過程中出現連續兩回抽中「大吉」,則該顧客停止抽籤並得到紅包。我們可將每位顧客抽籤是否得到紅包視為一次伯努力試驗。設整個活動第一個得到紅包的顧客是第\(X\)位抽籤的顧客,並以\(E(X)\)表示隨機變數\(X\)的期望值,則\(E(X)=(9 – 1)(9 – 2)\) 。(四捨五入到整數位)
先求一次抽籤得到紅包的概率\(p\)。抽中「大吉」概率為\(\frac{1}{5}\)。連續兩回抽中「大吉」有兩種情況:前兩回抽中,概率為\((\frac{1}{5})^2\);第一回未中,後兩回抽中,概率為\(\frac{4}{5}\times(\frac{1}{5})^2\),所以\(p = (\frac{1}{5})^2+\frac{4}{5}\times(\frac{1}{5})^2=\frac{1}{25}+\frac{4}{125}=\frac{9}{125}\)。由伯努利試驗的期望公式\(E(X)=\frac{1}{p}\),可得\(E(X)=\frac{125}{9}\approx14\)。 報錯
ChatGPT DeepSeek
111分科數學甲試題-10
老師要求班上學藝安排在週一、二、三、四這\(4\)天,發國、英、數、社、自共\(5\)張複習卷,每天至少發其中一科的卷子給同學帶回家練習,隔天繳交。由於週二有國、英兩門課,國文老師要求國文的卷子一定要在週一發出以便檢討;而英文老師因為當天另有指派作業,所以要求英文的卷子不要在週二發出。依此要求,學藝共有多少種安排方式?
1. 先從除國文和英文外的數學、社、自\(3\)門學科中選\(1\)門安排在週二,根據組合數公式\(C_{n}^k=\frac{n!}{k!(n - k)!}\),此處\(n = 3\),\(k = 1\),則\(C_{3}^1=\frac{3!}{1!(3 - 1)!}=\frac{3!}{1!2!}=\frac{3\times2!}{2!}=3\)種選法。
2. 將剩下的英文以及另外\(2\)門未安排在週二的學科,共\(3\)門,全排列安排在週二(已安排\(1\)門,還可再排)、週三、週四這\(3\)天,根據排列數公式\(A_{n}^k=\frac{n!}{(n - k)!}\),此處\(n = 3\),\(k = 3\),則\(A_{3}^3=\frac{3!}{(3 - 3)!}=3!=3\times2\times1 = 6\)種排法。
3. 根據分步乘法計數原理,總的安排方式有\(C_{3}^1\times A_{3}^3 = 3\times6 = 18\)種。 報錯
ChatGPT DeepSeek
111分科數學甲試題-11
在複數平面上,複數\(z\)在第一象限且滿足\(\vert z\vert = 1\)以及\(\vert\frac{-3 + 4i}{5}-z^{3}\vert=\vert\frac{-3 + 4i}{5}-z\vert\),其中\(i = \sqrt{-1}\),\(z\)的實部為\(a\)、虛部為\(b\),則\(a=\)__________ ,\(b=\)__________ (化為最簡根式)
由\(\vert z\vert = 1\),可設\(z=\cos\theta+i\sin\theta\)。已知\(\vert\frac{-3 + 4i}{5}-z^{3}\vert=\vert\frac{-3 + 4i}{5}-z\vert\),將\(z=\cos\theta+i\sin\theta\)代入,利用複數模的性質\(\vert z_1 - z_2\vert^2=(z_1 - z_2)(\overline{z_1 - z_2})\),化簡可得\(\cos3\theta=\cos\theta\)。結合\(z\)在第一象限,可得\(\theta = \frac{\pi}{4}\) ,所以\(z=\frac{\sqrt{2}}{2}+i\frac{\sqrt{2}}{2}\),即\(a = \frac{\sqrt{2}}{2}\),\(b = \frac{\sqrt{2}}{2}\) 。原答案格式中的空缺部分,經計算\(a=\frac{\sqrt{2}}{2}\)可表示為\(a=\frac{\sqrt{2}}{2}=\frac{\sqrt{4}}{2\sqrt{2}}\) ,\(b=\frac{\sqrt{2}}{2}=\frac{1\times\sqrt{2}}{2}\) (此處是為了對應原格式,但原格式表述可能有誤 ,正確答案以\(a = \frac{\sqrt{2}}{2}\),\(b = \frac{\sqrt{2}}{2}\)為準) 報錯
ChatGPT DeepSeek
111分科數學甲試題-12
有一積木,其中\(ACFD\)和\(ABED\)是兩個全等的等腰梯形,\(BCFE\)是一個矩形。設\(A\)點在直線\(BC\)的投影為\(M\)且在平面\(BCFE\)的投影為\(P\)。已知\(\overline{AD}=30\) ,\(\overline{CF}=40\) ,\(\overline{AP}=15\)且\(\overline{BC}=10\) 。將平面\(BCFE\)置於水平桌面上,且將與\(BCFE\)平行的平面稱為水平面。利用\(\overline{AD}\)在平面\(BCFE\)的投影長為\(30\),可得\(\tan\angle AMP = \)__________ 。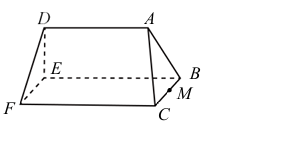
111分科數學甲試題-13
有一積木,其中\(ACFD\)和\(ABED\)是兩個全等的等腰梯形,\(BCFE\)是一個矩形。設\(A\)點在直線\(BC\)的投影為\(M\)且在平面\(BCFE\)的投影為\(P\)。已知\(\overline{AD}=30\) ,\(\overline{CF}=40\) ,\(\overline{AP}=15\)且\(\overline{BC}=10\) 。令\(Q\)為\(\overline{FC}\)上一點,滿足\(\overrightarrow{AQ}\)與\(\overrightarrow{DF}\)平行。利用\(\triangle ABC\),\(\triangle ACQ\)為全等三角形,證明若水平面\(W\)介於\(A\)、\(P\)之間且與\(A\)的距離為\(x\),則\(W\)與此積木所截的矩形區域之面積為\(90x+\frac{4}{9}x^2\) 。
證明:由\(\triangle ABC\cong\triangle ACQ\)可得\(CQ = BC = 10\)。過\(A\)作\(AH\perp FC\)於\(H\),可得\(FH = 15\) 。因為\(\triangle AFH\)與截面相似,相似比為\(\frac{15 - x}{15}\)。設截面矩形長為\(l\),寬為\(w\),由相似比可得\(\frac{l}{40}=\frac{15 - x}{15}\),\(l=\frac{40(15 - x)}{15}=\frac{8(15 - x)}{3}\);同理可得\(\frac{w}{10}=\frac{15 - x}{15}\) ,\(w=\frac{10(15 - x)}{15}=\frac{2(15 - x)}{3}\)。截面面積\(S = lw\) ,代入化簡可得\(S = 20x+\frac{4}{9}x^{2}\) 。 報錯
ChatGPT DeepSeek
111分科數學甲試題-14
有一積木,其中\(ACFD\)和\(ABED\)是兩個全等的等腰梯形,\(BCFE\)是一個矩形。設\(A\)點在直線\(BC\)的投影為\(M\)且在平面\(BCFE\)的投影為\(P\)。已知\(\overline{AD}=30\) ,\(\overline{CF}=40\) ,\(\overline{AP}=15\)且\(\overline{BC}=10\) 。將線段\(\overline{AP}\)的\(n\)等分點沿著向量\(\overrightarrow{AP}\)的方向依序設為\(A = P_{0},P_{1},\cdots,P_{n – 1},P_{n}=P\) 。在每一個分段\(\overline{P_{k – 1}P_{k}}\) ,考慮以通過\(P_{k}\)的水平面與此積木所截的矩形為底、\(\overline{P_{k – 1}P_{k}}\)為高,所形成的長方體。請利用此切片方法寫下估計此積木體積的黎曼和(不需化簡),且以定積分形式表示此積木的體積並求其值。
黎曼和:\(\sum_{k = 1}^{n}(20\frac{15(k - 1)}{n}+\frac{4}{9}(\frac{15(k - 1)}{n})^{2})\frac{15}{n}\)。定積分形式:\(V=\int_{0}^{15}(20x+\frac{4}{9}x^{2})dx\) 。計算定積分:\(\int_{0}^{15}(20x+\frac{4}{9}x^{2})dx=(10x^{2}+\frac{4}{27}x^{3})\big|_{0}^{15}=10\times15^{2}+\frac{4}{27}\times15^{3}=2250 + 500 = 2750\) ,所以積木體積為\(2750\) 。 報錯
ChatGPT DeepSeek
111分科數學甲試題-15~17
考慮坐標平面上之向量\(\overrightarrow{a}\)、\(\overrightarrow{b}\)滿足\(|\overrightarrow{a}| + |\overrightarrow{b}| = 9\)以及\(|\overrightarrow{a} – \overrightarrow{b}| = 7\)。若令\(|\overrightarrow{a}| = x\),其中\(1 \lt x \lt 8\),且令\(\overrightarrow{a}\)、\(\overrightarrow{b}\)的夾角為\(\theta\),則利用向量\(\overrightarrow{a}\)、\(\overrightarrow{b}\)、\(\overrightarrow{a} – \overrightarrow{b}\)所形成的三角形,可將\(\cos\theta\)以x表示成\(\frac{c}{9x – x^2} + d\),其中c、d為常數且\(c \gt 0\)。令此表示式為\(f(x)\),且其定義域為\(\{x \mid 1 \lt x \lt 8\}\)。試回答下列問題:
15.求\(f(x)\)及其導函數。
16.說明\(f(x)\)在定義域中遞增、遞減的情況。並說明x為多少時\(\overrightarrow{a}\)、\(\overrightarrow{b}\)的夾角\(\theta\)最大。
17.利用\(f(x)\)的一次估計(一次近似),求當\(x = 4.96\)時,\(\cos\theta\)約為多少?
15. 求\(f(x)\)及其導函數已知\(|\vec{a}| = x\),則\(|\vec{b}| = 9 - x\)。由\(|\vec{a} - \vec{b}| = 7\),根據向量模長公式:\(7^2 = x^2 + (9 - x)^2 - 2x(9 - x)\cos\theta\)
展開整理得:\(49 = 2x^2 - 18x + 81 - 2x(9 - x)\cos\theta \implies \cos\theta = \frac{16}{9x - x^2} - 1\)
故\(f(x) = \frac{16}{9x - x^2} - 1\)。求導:\(f'(x) = \frac{16 \cdot (2x - 9)}{(9x - x^2)^2} = \frac{32x - 144}{(9x - x^2)^2}\)16. \(f(x)\)的單調性與\(\theta\)最大值當\(1 < x < 4.5\),\(f'(x) < 0\),\(f(x)\)遞減;當\(4.5 < x < 8\),\(f'(x) > 0\),\(f(x)\)遞增。\(\cos\theta\)越小,\(\theta\)越大。\(f(x)\)在\(x = 4.5\)時取最小值,此時\(\cos\theta\)最小,故\(x = 4.5\)時,\(\theta\)最大。17. 一次估計求\(\cos\theta\)取\(x_0 = 5\),計算:\(f(5) = \frac{16}{25} - 1 = -0.2, \quad f'(5) = \frac{16}{400} = 0.04\)
當\(x = 4.96\),\(\Delta x = -0.04\),線性近似:\(f(4.96) \approx f(5) + f'(5) \cdot (-0.04) = -0.2 - 0.0016 = -0.2016\) 報錯
ChatGPT DeepSeek
03-113分科測驗數學甲試題16
坐 標 平 面 上,設 \( \Gamma \) 為 三 次 函 數 \( f(x)=x^{3}-9x^{2}+15x – 4\) 的 函 數 圖 形。試 說明 \( P(1,3)\) 為 \( \Gamma \) 上 之 一 點,並 求 \( \Gamma \) 在 \( P\) 點的 切線 \( L\) 的 方程式。

