112學測數學A
112學測數學A考科-02
112學測數學A考科-03
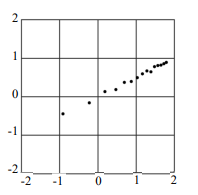 某生推導出兩物理量 \( s \),\( t \) 應滿足一等式。為了驗證其理論,他做了實驗得到15筆兩物理量的數據 \((s_k, t_k), k=1, \ldots, 15\) 。老師建議他將其中的 \( t_k \) 先取對數,在坐標平面上標出對應的點 \((s_k, \log t_k), k=1, \ldots, 15\) ,如右圖所示;其中第一個數據為橫軸坐標,第二個數據為縱軸坐標。利用迴歸直線分析,某生印證了其理論。
某生推導出兩物理量 \( s \),\( t \) 應滿足一等式。為了驗證其理論,他做了實驗得到15筆兩物理量的數據 \((s_k, t_k), k=1, \ldots, 15\) 。老師建議他將其中的 \( t_k \) 先取對數,在坐標平面上標出對應的點 \((s_k, \log t_k), k=1, \ldots, 15\) ,如右圖所示;其中第一個數據為橫軸坐標,第二個數據為縱軸坐標。利用迴歸直線分析,某生印證了其理論。
試問該生所得 \( s \),\( t \) 的關係式最可能為下列哪一選項?
\[(1) \quad s = 2t \quad (2) \quad s = 3t \quad (3) \quad t = 10^5\]
\[(4) \quad t^2 = 10^5 \quad (5) \quad t^3 = 10^5\]
112學測數學A考科-04
將數字1、2、3、⋯⋯、9等9個數字排成九位數(數字不得重複),使得前5位從左至右遞增,且後5位從左至右遞減。試問共有幾個滿足條件的九位數?
\[(1) \quad \frac{81}{414!} \quad (2) \quad \frac{81}{513!} \quad (3) \quad \frac{91}{514!} \quad (4) \quad \frac{81}{51} \quad (5) \quad \frac{91}{51}\]
112學測數學A考科-05
已知坐標空間中 \( P \cdot Q \cdot R \) 為平面 \( 2x-3y+5z=\sqrt{7} \) 上不共線三點。
令 \( \overrightarrow{PQ}=(a_1, b_1, c_1) \),\( \overrightarrow{PR}=(a_2, b_2, c_2) \)。試選出下列行列式中絕對值為最大的選項。
(1)
\[\begin{vmatrix}
-1 & 1 & 1 \\
a_1 & b_1 & c_1 \\
a_2 & b_2 & c_2
\end{vmatrix}\]
(2)
\[\begin{vmatrix}
1 & -1 & 1 \\
a_1 & b_1 & c_1 \\
a_2 & b_2 & c_2
\end{vmatrix}\]
(3)
\[\begin{vmatrix}
1 & 1 & -1 \\
a_1 & b_1 & c_1 \\
a_2 & b_2 & c_2
\end{vmatrix}\]
(4)
\[\begin{vmatrix}
-1 & -1 & 1 \\
a_1 & b_1 & c_1 \\
a_2 & b_2 & c_2
\end{vmatrix}\]
(5)
\[\begin{vmatrix}
-1 & -1 & -1 \\
a_1 & b_1 & c_1 \\
a_2 & b_2 & c_2
\end{vmatrix}\]
行列式絕對值代表由 \( \overrightarrow{PQ} \)、\( \overrightarrow{PR} \)、\( \overset{\rightharpoonup}{u} \) 所張平行六面體體積,與 \( |\overset{\rightharpoonup}{u} \cdot \overset{\rightharpoonup}{n}| \) 成正比,其中 \( \overset{\rightharpoonup}{n} = (2, -3, 5) \) 為法向量
計算各選項 \( |\overset{\rightharpoonup}{u} \cdot \overset{\rightharpoonup}{n}| \):(1)0 (2)10 (3)6 (4)6 (5)4,最大值為10
故選(2) 報錯
ChatGPT DeepSeek
112學測數學A考科-06
坐標空間中,考慮邊長為 1 的正立方體,固定一頂點 \( O \)。從 \( O \) 以外的七個頂點隨機選取相異兩點,設此兩點為 \( P \cdot Q \),試問所得的內積 \( \overrightarrow{OP} \cdot \overrightarrow{OQ} \) 之期望值為下列哪一個選項?
(1) \(\frac{4}{7}\) (2) \(\frac{5}{7}\) (3) \(\frac{6}{7}\) (4) \(\frac{1}{7}\) (5) \(\frac{8}{7}\)
112學測數學A考科-07
某公司有甲、乙兩新進員工,兩人同時問人職且起薪相同。公司承諾給甲、乙兩員工調薪的方式如下:
甲:工作滿 3 個月,下個月開始月薪增加 200 元;以後再每滿 3 個月皆依此方式調薪。
乙:工作滿 12 個月,下個月開始月薪增加 1000 元;以後再每滿 12 個月皆依此方式調薪。
根據以上敘述,試選出正確的選項。
(1) 甲工作滿 8 個月後,第 9 個月的月薪比第 1 個月的月薪增加 600 元
(2) 工作滿一年後,第 13 個月甲的月薪比乙的月薪高
(3) 工作滿 18 個月後,第 19 個月甲的月薪比乙的月薪高
(4) 工作滿 18 個月時,甲總共領到的薪水比乙總共領到的薪水少
(5) 工作滿兩年後,在第 3 年的 12 個月中,恰有 3 個月甲的月薪比乙的月薪高
112學測數學A考科-08
某抽獎遊戲單次中獎機率為0.1,每次中獎與否皆為獨立事件。對每一正整數 \( n \),令 \( p_n \) 為玩此遊戲 \( n \) 次至少中獎1次的機率。試選出正確的選項。
(1) \( p_{n+1} \gt p_n \)
(2) \( p_3 = 0.3 \)
(3) \( \langle p_n \rangle \) 為等差數列
(4)玩此遊戲兩次以上,第一次未中獎且第二次中獎的機率等於 \( p_2 – p_1 \)
(5)玩此遊戲 \( n \) 次且 \( n \geq 2 \) 時,至少中獎2次的機率等於 \( 2p_n \)
112學測數學A考科-09
設 \( a_1, a_2, a_3, \ldots, a_n \) 是首項為3且公比為\(3\sqrt{3}\)的等比數列。試選出滿足不等式
\[\log_3 a_1 – \log_3 a_2 + \log_3 a_3 – \log_3 a_4 + \cdots + (-1)^{n+1} \log_3 a_n \gt 18\]
的項數 \( n \) 之可能選項。
(1) 23 (2) 24 (3) 25 (4) 26 (5) 27
\( a_n = 3 \cdot (3\sqrt{3})^{n-1} = 3^{\frac{3n-1}{2}} \Rightarrow \log_3 a_n = \frac{3n-1}{2} \)
交錯和 \( S_n = \frac{1}{2}[2 - 5 + 8 - 11 + \cdots + (-1)^{n+1}(3n-1)] \)
當 \( n \) 為奇數時,\( S_n = \frac{1}{2}[2 + 3 \times \frac{n-1}{2}] \gt 18 \Rightarrow n \gt 23\frac{2}{3} \)
又 \( n \) 為奇數,故選(3)(5) 報錯
ChatGPT DeepSeek
112學測數學A考科-10
考慮坐標平面上的直線 \( L : 5y + (2k-4)x – 10k = 0 \) (其中 \( k \) 為一實數),以及長方形 \( OABC \),其頂點坐標為 \( O(0, 0) \)、\( A(10, 0) \)、\( B(10, 6) \)、\( C(0, 6) \)。設 \( L \) 分別交直線 \( OC \)、直線 \( AB \) 於點 \( D \)、\( E \)。試選出正確的選項。
(1)當 \( k = 4 \) 時,直線 \( L \) 通過點 \( A \)
(2)若直線 \( L \) 通過點 \( C \),則 \( L \) 的斜率為 \( -\frac{5}{2} \)
(3)若點 \( D \) 在線段 \( OC \) 上,則 \( 0 \leq k \leq 3 \)
(4)若 \( k = \frac{1}{2} \),則線段 \( DE \) 在長方形 \( OABC \) 內部(含邊界)
(5)若線段 \( DE \) 在長方形 \( OABC \) 內部(含邊界),則 \( L \) 的斜率可能為 \( \frac{3}{10} \)
(1)○:\( k=4 \)時,\( L: 5y+4x-40=0 \) 過 \( A(10,0) \)
(2)×:過 \( C(0,6) \) 得 \( k=3 \),斜率 \( m = -\frac{2}{5} \)
(3)○:\( D(0,2k) \),在 \( \overline{OC} \) 上 ⇒ \( 0 \leq 2k \leq 6 \Rightarrow 0 \leq k \leq 3 \)
(4)×:\( k=\frac{1}{2} \)時,\( E(10,7) \) 不在長方形內部
(5)○:\( E(10,8-2k) \),\( D(0,2k) \) 在長方形內部 ⇒ \( 1 \leq k \leq 3 \),當 \( m = \frac{3}{10} \) 時 \( k = \frac{5}{4} \) 符合
故選(1)(3)(5) 報錯
ChatGPT DeepSeek