〈114學測數學A 〉彙整頁面 - 第 2 頁，總計 2 頁

114學測數學A考科_11

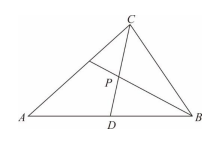
在 \(\triangle ABC\) 中，\(\overline{AB} = 6\)，\(\overline{AC} = 5\)，\(\overline{BC} = 4\)。令 \(\overline{AB}\) 中點為 \(D\)，\(P\) 為 \(\angle ABC\) 之角平分線與 \(\overline{CD}\) 之交點，如右圖所示。試選出正確的選項。
(1) \(\overline{CP} = \frac{3}{7}\overline{CD}\)
(2) \(\overset{\rightharpoonup}{AP} = \frac{3}{7}\overset{\rightharpoonup}{AB} + \frac{2}{7}\overset{\rightharpoonup}{AC}\)
(3) \(\cos \angle BAC = \frac{3}{4}\)
(4) \(\triangle ACP\) 面積為 \(\frac{15}{14}\sqrt{7}\)
(5) (內積) \(\overset{\rightharpoonup}{AP} \cdot \overset{\rightharpoonup}{AC} = \frac{120}{7}\)

答案

(1) ✗：\(\overline{CP}=\frac{4}{7}\overline{CD}\)；(2) ✗：\(\overset{\rightharpoonup}{AP}=\frac{2}{7}\overset{\rightharpoonup}{AB}+\frac{3}{7}\overset{\rightharpoonup}{AC}\)；
(3) ✓：餘弦定理得 \(\cos \angle BAC=\frac{3}{4}\)；(4) ✓：面積計算得 \(\frac{15\sqrt{7}}{14}\)；
(5) ✓：內積計算得 \(\frac{120}{7}\)。
故選(3)(4)(5)。報錯
 ChatGPT DeepSeek

加最愛

114學測數學A考科_12

某種合金由甲和乙兩種金屬組成，某生想知道其中金屬比例與合金的波長關係。他做實驗測量「甲占比為 \(x\%\) 的合金所對應的波長 \(y\)（單位：奈米）」，並將得到的20筆數據 \((x_k, y_k)\)，\(k=1, \ldots, 20\)，在 \(xy\) 平面上標出對應的點，其迴歸直線（最適直線）為 \(y=21.3x-40\)。為符合投稿規範，須將報告描述為「乙占比為 \(u\%\) 的合金所對應的波長 \(v\)（單位：微米）」，他將數據 \((x_k, y_k)\) 轉換為 \((u_k, v_k)\)，\(k=1, \ldots, 20\)，得到在 \(uv\) 平面的迴歸直線為 \(v=au+b\)。已知1奈米=\(10^{-9}\)公尺，1微米=\(10^{-6}\)公尺。試選出正確的選項。
(1) \(u_k=100-x_k\)，\(k=1, \ldots, 20\)
(2) \(v_k=1000y_k\)，\(k=1, \ldots, 20\)
(3) \(u_1, u_2, u_3, \ldots, u_{20}\) 的標準差等於 \(x_1, x_2, x_3, \ldots, x_{20}\) 的標準差
(4) \(b=2.09\)
(5) 某生發現有另一筆數據 \((u_{21}, v_{21})\)，且滿足 \(v_{21}=au_{21}+b\)；若將這21筆數據 \((u_k, v_k)\)，\(k=1, \ldots, 21\)，在 \(uv\) 平面上標出對應的點，則其迴歸直線仍為 \(v=au+b\)

答案

(1) ✓：\(u=100-x\)；(2) ✗：\(v=\frac{y}{1000}\)；(3) ✓：標準差不變；
(4) ✓：代入得 \(b=2.09\)；(5) ✓：新點在直線上，迴歸直線不變。
故選(1)(3)(4)(5)。報錯
 ChatGPT DeepSeek

加最愛

114學測數學A考科_13

已知實係數三次多項式 \(f(x)\) 除以 \(x+6\) 得商式 \(q(x)\) 和餘式 3。若 \(q(x)\) 在 \(x=-6\) 有最大值 8，則 \(y=f(x)\) 圖形的對稱中心坐標為 \((\)__________\(,\)__________\()\)。

答案

設 \(q(x)=a(x+6)^2+8\) (\(a \lt 0\))，則 \(f(x)=(x+6)q(x)+3=a(x+6)^3+8(x+6)+3\)。
對稱中心為 \((-6,3)\)。報錯
 ChatGPT DeepSeek

加最愛

114學測數學A考科_14

坐標空間中，已知點 \(A\) 的坐標為 \((a, b, c)\)，其中 \(a\)，\(b\)，\(c\) 皆為小於 0 的實數，且知點 \(A\) 與三平面 \(E_1: 4y+3z=2\)、\(E_2: 3y+4z=-5\)、\(E_3: x+2y+2z=-2\) 的距離都是 6，則 \(a+b+c=\) __________。

答案

由點到平面距離公式列出方程組：
\(\frac{|4b+3z-2|}{5}=6\)，\(\frac{|3b+4z+5|}{5}=6\)，\(\frac{|x+2y+2z+2|}{3}=6\)。
解得 \(a=-2\)，\(b+c=-9\)，故 \(a+b+c=-11\)。報錯
 ChatGPT DeepSeek

加最愛

114學測數學A考科_15

假日市集有個攤位推出「試試手氣，定價 480 元的可愛玩偶最低只要 240 元」。規則為：顧客投擲一枚均勻硬幣至多 5 次，前 3 次連續擲得 3 個正面者則只能以 240 元購得一個玩偶，擲到第 4 次才累積得 3 個正面者則只能以 320 元購得一個，擲到第 5 次才累積得 3 個正面者則只能以 400 元購得一個；5 次投完仍未累積 3 個正面者則只能以 480 元購得一個。參與此遊戲的顧客購得一個玩偶所花金額的期望值為 __________ 元。

答案

計算各情況機率：
240元：\(\left(\frac{1}{2}\right)^3=\frac{1}{8}\)；
320元：\(C^3_2\left(\frac{1}{2}\right)^4=\frac{3}{16}\)；
400元：\(C^4_2\left(\frac{1}{2}\right)^5=\frac{3}{16}\)；
480元：\(1-\frac{1}{8}-\frac{3}{16}-\frac{3}{16}=\frac{1}{2}\)。
期望值 \(=240\times\frac{1}{8}+320\times\frac{3}{16}+400\times\frac{3}{16}+480\times\frac{1}{2}=405\) 元。報錯
 ChatGPT DeepSeek

加最愛

114學測數學A考科_16

坐標平面上，設 \(L_1\)、\(L_2\) 為通過點 \((3, 1)\) 且斜率分別為 \(m\)、\(-m\) 的兩條直線，其中 \(m\) 為一實數。另設 \(\Gamma\) 為圓心在原點的一個圓。已知 \(\Gamma\) 與 \(L_1\) 交於相異兩點 \(A\)、\(B\)，且知圓心到 \(L_1\) 的距離為 1，又 \(\Gamma\) 與 \(L_2\) 相切，則弦 \(\overline{AB}\) 的長度為 __________。（化為最簡分數）

答案

圓 \(\Gamma: x^2+y^2=r^2\)，\(L_1: mx-y-3m+1=0\)，圓心到 \(L_1\) 距離為 1 得 \(m=\frac{3}{4}\)。
代入 \(L_2\) 與圓相切得 \(r=\frac{13}{5}\)，弦長 \(\overline{AB}=2\sqrt{r^2-1^2}=\frac{24}{5}\)。報錯
 ChatGPT DeepSeek

加最愛

114學測數學A考科_17

\(\triangle ABC\) 中，已知 \(\overline{AB} = \overline{BC} = 3\)，\(\cos \angle ABC = -\frac{1}{8}\)。在 \(\triangle ABC\) 的外接圓上有一點 \(D\) 滿足 \(\overline{BD} = 4\)，且 \(\overline{AD} \leq \overline{CD}\)，則 \(\overline{CD} = \) __________。（化為最簡根式）

答案

由餘弦定理得 \(\overline{AC}=\sqrt{3^2+3^2-2\cdot3\cdot3\cdot(-\frac{1}{8})}=\frac{3\sqrt{10}}{2}\)。
在 \(\triangle BCD\) 中，利用圓周角相等及餘弦定理得 \(\overline{CD}^2-6\overline{CD}+7=0\)，解得 \(\overline{CD}=3+\sqrt{2}\)（因 \(\overline{AD} \leq \overline{CD}\)）。報錯
 ChatGPT DeepSeek

加最愛

114學測數學A考科_18

18-20 題為題組
已知 \(A = \begin{bmatrix} a_1 & a_2 \\ a_3 & a_4 \end{bmatrix}\)，\(B = \begin{bmatrix} b_1 & b_2 \\ b_3 & b_4 \end{bmatrix}\) 皆為坐標平面上以原點 \(O\) 為中心，逆時針旋轉一銳角的旋轉矩陣，且滿足 \(A^2 = B^3 = \begin{bmatrix} 0 & c \\ 1 & d \end{bmatrix}\)，其中 \(c \cdot d\) 為實數。
設點 \(P(1, 1)\) 經 \(A^3\) 變換後為點 \(Q\)，且點 \(Q\) 經 \(B^4\) 變換後為點 \(R\)。根據上述，試回答下列問題。
18. 試問 \(c\) 之值為何？(單選題，3分)
(1) 0 (2) -1 (3) 1 (4) \(-\frac{1}{2}\) (5) \(\frac{1}{2}\)

答案

令 \(A\) 為旋轉 \(\theta_1\) 的矩陣，則 \(A^2\) 為旋轉 \(2\theta_1\) 的矩陣。
由 \(A^2=\begin{bmatrix} 0 & c \\ 1 & d \end{bmatrix}\) 得 \(\cos 2\theta_1=0\)，\(\sin 2\theta_1=1\)，故 \(c=-\sin 2\theta_1=-1\)，選(2)。報錯
 ChatGPT DeepSeek

加最愛

114學測數學A考科_19

18-20 題為題組
19. 試求點 \(Q\) 的坐標，以及 \(\overset{\rightharpoonup}{OR}\) 與向量 \((1, 0)\) 的夾角。(非選擇題，6分)

答案

由18題得 \(\theta_1=45^\circ\)，\(A^3\) 為旋轉 \(135^\circ\) 矩陣，將 \(P(1,1)\) 變換得 \(Q(-\sqrt{2},0)\)。
由 \(B^3\) 得 \(\theta_2=30^\circ\)，\(B^4\) 為旋轉 \(120^\circ\) 矩陣，將 \(Q\) 變換得 \(R(-\frac{\sqrt{2}}{2},-\frac{\sqrt{6}}{2})\)。
計算 \(\overset{\rightharpoonup}{OR}\) 與 \((1,0)\) 夾角：\(\cos\theta=\frac{1}{2}\)，\(\theta=60^\circ\)。報錯
 ChatGPT DeepSeek

加最愛

114學測數學A考科_20

18-20 題為題組
20. 設 \(L\) 為過點 \(P\) 且與直線 \(OQ\) 平行的直線，點 \(S\) 為 \(L\) 和直線 \(OR\) 的交點，試求 \(\angle OSP\)，並求點 \(S\) 的坐標。（非選擇題，6分）

答案

\(L\) 過 \(P(1,1)\) 且平行 \(OQ\)（斜率 0），故 \(L: y=1\)。
直線 \(OR\) 斜率為 \(\sqrt{3}\)，方程為 \(y=\sqrt{3}x\)。
聯立解得 \(S(-\frac{\sqrt{3}}{3},1)\)，\(\angle OSP = 60^\circ\)。報錯
 ChatGPT DeepSeek

加最愛

Saved articles