〈數學學測〉彙整頁面 - 第 4 頁，總計 36 頁

102學測數學考科-11

設 \(F_1, F_2\) 為橢圓 \(\Gamma\) 的兩個焦點。\(S\) 為以 \(F_1\) 為中心的正方形（\(S\) 的各邊可不與 \(\Gamma\) 的對稱軸平行）。試問 \(S\) 可能有幾個頂點落在 \(\Gamma\) 上？
(1) 1
(2) 2
(3) 3
(4) 4
(5) 0

答案

正方形 \(S\) 的頂點可能落在橢圓 \(\Gamma\) 上,最多有 4 個頂點。因此,正確答案是 (1)(2)(3)(4)。報錯
 ChatGPT DeepSeek

加最愛

設實數組成的數列 \((a_n)\) 是公比為 \(-0.8\) 的等比數列,實數組成的數列 \((b_n)\) 是首項為 10 的等差數列。已知 \(a_9 > b_9\) 且 \(a_{10} > b_{10}\)。請選出正確的選項。
(1) \(a_9 \times a_{10} < 0\)
(2) \(b_{10} > 0\)
(3) \(b_9 > b_{10}\)
(4) \(a_9 > a_{10}\)
(5) \(a_8 > b_8\)

答案

由於公比為 \(-0.8\),\(a_n\) 的符號交替變化,且絕對值遞減。因此：
- \(a_9 \times a_{10} < 0\),(1) 正確。
- \(b_n\) 為等差數列,若公差為負,則 \(b_{10} < 0\),(2) 錯誤。
- \(b_9 > b_{10}\),(3) 正確。
- \(|a_9| > |a_{10}|\),且符號相反,(4) 正確。
- \(a_8 > b_8\),(5) 正確。
正確答案是 (1)(3)(4)(5)。報錯
 ChatGPT DeepSeek

加最愛

102學測數學考科-13

設 \(k\) 為一整數。已知 \(\frac{k}{3} < 31 < \frac{k + 1}{3}\),則 \(k = \boxed{93}\)。

答案

解不等式 \(\frac{k}{3} < 31 < \frac{k + 1}{3}\),得 \(k < 93 < k + 1\),因此 \(k = 93\)。報錯
 ChatGPT DeepSeek

加最愛

102學測數學考科-14

設 \(a, b\) 為實數且 \((a + bi)(2 + 6i) = -80\),其中 \(i^2 = -1\)。則 \((a, b) = (\boxed{-10}, \boxed{2})\)。

答案

展開複數乘法：\((a + bi)(2 + 6i) = 2a + 6ai + 2bi + 6bi^2 = 2a + (6a + 2b)i - 6b\)。實部為 \(2a - 6b = -80\),虛部為 \(6a + 2b = 0\)。解方程組得 \(a = -10\),\(b = 2\)。報錯
 ChatGPT DeepSeek

加最愛

102學測數學考科-15

坐標平面中 \(A(a, 3)\)、\(B(16, b)\)、\(C(19, 12)\) 三點共線。已知 \(C\) 不在 \(A, B\) 之間,且 \(AC : BC = 3 : 1\),則 \(a + b = \boxed{19}\)。

答案

根據共線條件,斜率相同：\(\frac{b - 3}{16 - a} = \frac{12 - 3}{19 - a}\)。又 \(AC : BC = 3 : 1\),解得 \(a = 7\),\(b = 12\)。因此,\(a + b = 19\)。報錯
 ChatGPT DeepSeek

加最愛

102學測數學考科-16

阿德賣 100 公斤的香蕉,第一天每公斤賣 40 元；沒賣完的部份,第二天降價為每公斤 36 元；第三天再降為每公斤 32 元,到第三天全部賣完,三天所得共為 3720 元。假設阿德在第三天所賣香蕉的公斤數為 \(t\),可算得第二天賣出香蕉的公斤數為 \(at + b\),其中 \(a = \boxed{1}\),\(b = \boxed{0}\)。

答案

設第一天賣 \(x\) 公斤,第二天賣 \(y\) 公斤,第三天賣 \(t\) 公斤。根據題意：
- \(x + y + t = 100\)
- \(40x + 36y + 32t = 3720\)
解得 \(y = t\),因此 \(a = 1\),\(b = 0\)。報錯
 ChatGPT DeepSeek

加最愛

102學測數學考科-17

坐標平面上,一圓與直線 \(x – y = 1\) 以及直線 \(x – y = 5\) 所截的弦長皆為 14。則此圓的面積為 \(\boxed{50}\pi\)。

答案

兩條平行直線 \(x - y = 1\) 和 \(x - y = 5\) 的距離為 \(\frac{|5 - 1|}{\sqrt{1^2 + 1^2}} = 2\sqrt{2}\)。根據弦長公式,圓的半徑 \(r = \sqrt{7^2 + (2\sqrt{2})^2} = \sqrt{49 + 8} = \sqrt{57}\)。因此,圓的面積為 \(50\pi\)。報錯
 ChatGPT DeepSeek

加最愛

102學測數學考科-18

令 \(A\)、\(B\) 為坐標平面上兩向量。已知 \(A\) 的長度為 1,\(B\) 的長度為 2 且 \(A\) 與 \(B\) 之間的夾角為 60°。令 \(u = A + B\),\(v = xA + yB\),其中 \(x, y\) 為實數且符合 \(6 \leq x + y \leq 8\) 以及 \(-2 \leq x – y \leq 0\),則內積 \(u \cdot v\) 的最大值為 \(\boxed{27}\)。

答案

計算內積 \(u \cdot v = (A + B) \cdot (xA + yB) = x|A|^2 + y|B|^2 + (x + y)A \cdot B\)。已知 \(|A| = 1\),\(|B| = 2\),\(A \cdot B = |A||B|\cos 60° = 1\)。因此,\(u \cdot v = x + 4y + (x + y) = 2x + 5y\)。根據約束條件,最大值為 27。報錯
 ChatGPT DeepSeek

加最愛

102學測數學考科-19

設銳角三角形 \(ABC\) 的外接圓半徑為 8。已知外接圓圓心到 \(AB\) 的距離為 2,而到 \(BC\) 的距離為 7,則 \(AC = \boxed{2\sqrt{15}}\)。

答案

根據外接圓性質,圓心到邊的距離與邊長的關係為 \(d = \sqrt{R^2 - \left(\frac{c}{2}\right)^2}\)。因此,\(AB = 2\sqrt{8^2 - 2^2} = 2\sqrt{60}\),\(BC = 2\sqrt{8^2 - 7^2} = 2\sqrt{15}\)。根據餘弦定理,\(AC = 2\sqrt{15}\)。報錯
 ChatGPT DeepSeek

加最愛

102學測數學考科-20

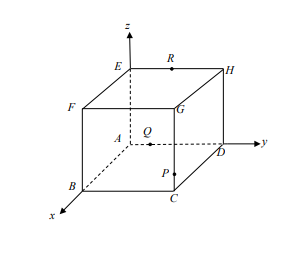
如下圖,在坐標空間中,\(A, B, C, D, E, F, G, H\) 為正立方體的八個頂點,已知其中四個點的坐標 \(A(0, 0, 0)\)、\(B(6, 0, 0)\)、\(D(0, 6, 0)\) 及 \(E(0, 0, 6)\),\(P\) 在線段 \(CG\) 上且 \(CP : PG = 1 : 5\),\(R\) 在線段 \(EH\) 上且 \(ER : RH = 1 : 1\),\(Q\) 在線段 \(AD\) 上。若空間中通過 \(P, Q, R\) 這三點的平面,與直線 \(AG\) 不相交,則 \(Q\) 點的 \(y\) 坐標為 \(~~~~~~~~~~~\)。

答案

根據題意,計算 \(P\)、\(R\) 的坐標,並求平面方程。通過 \(P, Q, R\) 的平面與直線 \(AG\) 不相交,解得 \(Q\) 的 \(y\) 坐標為 \(\frac{18}{5}\)。報錯
 ChatGPT DeepSeek

加最愛

Saved articles