便利商店因週年慶而提供折扣優惠,只要消費滿99元就可從紙盒中隨機抽球來決定該筆消費的折扣數(每顆球被抽到的機率相等)。店家已在盒中放了9顆球,其中寫著6折和7折的各有1顆、9折2顆、95折5顆。令隨機變數 \( X \) 代表消費100元的顧客在折扣後需要付的金額(元),若店家想再加入一球使得 \( X \) 的期望值等於86元,則新加入的那顆球上面所寫的折扣數應為下列哪一個選項?
(1) 65折
(2) 75折
(3) 8折
(4) 85折
(5) 9折
109指考數乙(補考)
109指考數學乙(補考)試題-02
在坐標平面上,\( O \) 為原點,考慮直線 \( L_1: 5x+3y=5 \) 與直線 \( L_2: 3x+2y=6-2a \),其中 \( a \) 為實數。若直線 \( L: 2x+y=3 \) 分別與直線 \( L_1 \) 及直線 \( L_2 \) 交於點 \( A \) 及點 \( B \),則三角形 \( OAB \) 的面積為下列哪一個選項?
(1) \( \frac{1}{2} |a-2| \)
(2) \( |a-2| \)
(3) \( 2|a-2| \)
(4) \( 3|a-2| \)
(5) \( 6|a-2| \)
求A點:解 \( \begin{cases} 5x+3y=5 \\ 2x+y=3 \end{cases} \),得 \( x=4 \),\( y=-5 \),故 \( A(4,-5) \)
求B點:解 \( \begin{cases} 3x+2y=6-2a \\ 2x+y=3 \end{cases} \),得 \( x=2a \),\( y=3-4a \),故 \( B(2a,3-4a) \)
三角形OAB面積 = \( \frac{1}{2} |x_A y_B - x_B y_A| = \frac{1}{2} |4(3-4a) - 2a(-5)| = \frac{1}{2} |12-16a+10a| = \frac{1}{2} |12-6a| = 3|2-a| = 3|a-2| \)
答案:(4) 報錯
ChatGPT DeepSeek
109指考數學乙(補考)試題-03
下列矩陣中,試選出矩陣乘法有意義且等式正確的選項。(註:選項中的[-1]與[-5]皆為一階方陣)
(1) \( [1 \quad 2][-1]=[-1 \quad -2] \)
(2) \( [-1][1 \quad 2]=[\begin{matrix} -1 \\ -2 \end{matrix}] \)
(3) \( \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}[5 \quad 6]=[17 \quad 39] \)
(4) \( \begin{bmatrix} 1 \\ 2 \end{bmatrix}[-1 \quad -2]=[-5] \)
(5) \( [-1 \quad 1]\begin{bmatrix} 1 & 109 \\ 0 & -1 \end{bmatrix}=[-1 \quad -110] \)
(1) \( 1\times2 \) 矩陣乘 \( 1\times1 \) 矩陣,維度不符
(2) \( 1\times1 \) 乘 \( 1\times2 \) 得 \( 1\times2 \),但結果寫成 \( 2\times1 \),錯誤
(3) \( 2\times2 \) 乘 \( 1\times2 \),維度不符
(4) \( 2\times1 \) 乘 \( 1\times2 \) 得 \( 2\times2 \),但結果寫成 \( 1\times1 \),錯誤
(5) \( 1\times2 \) 乘 \( 2\times2 \) 得 \( 1\times2 \),計算:\( [-1\times1+1\times0, -1\times109+1\times(-1)] = [-1, -110] \),正確
答案:(5) 報錯
ChatGPT DeepSeek
109指考數學乙(補考)試題-04
坐標平面上,設 \( a, b \) 為實數,已知目標函數 \( ax + by \) 在平面區域 \(\Omega\):\(\begin{cases} 4x + y \leq 16 \\ -2x + 3y \leq 6 \\ x \geq 0 \\ y \geq 0 \end{cases}\)的最大值為12,且取得最大值的點不在坐標軸上。試選出正確的選項。
(1) \( 4a + 3b = 12 \)
(2) \( -\frac{a}{b} > -3 \)
(3) \( -\frac{a}{b} < \frac{2}{3} \)
(4) \( b \)可能為\(-3\)
(5) \( b \)可能為\( 1 \)
區域頂點:\( (0,0) \)、\( (4,0) \)、\( (0,2) \)、交點 \( 4x+y=16 \) 與 \( -2x+3y=6 \) 得 \( (3,4) \)
最大值在 \( (3,4) \) 且不在坐標軸上,故 \( 3a+4b=12 \)
(1) 錯誤,應為 \( 3a+4b=12 \)
目標函數斜率 \( -\frac{a}{b} \) 介於邊界斜率之間:\( -4 < -\frac{a}{b} < \frac{2}{3} \)
(2) \( -\frac{a}{b} > -3 \) 不一定成立
(3) \( -\frac{a}{b} < \frac{2}{3} \) 正確
(4) 若 \( b=-3 \),由 \( 3a+4(-3)=12 \) 得 \( a=8 \),斜率 \( -\frac{8}{-3}=\frac{8}{3} \),不在範圍內
(5) 若 \( b=1 \),由 \( 3a+4=12 \) 得 \( a=\frac{8}{3} \),斜率 \( -\frac{8}{3} \),不在範圍內
答案:(3) 報錯
ChatGPT DeepSeek
109指考數學乙(補考)試題-05
當我們打電話到大公司時,電話會透過公司的交換機轉接到所接的號碼或分機,這個時候就會有等待接通的時間。實際測試發現,如果等待時間小於或等於0.8秒,打電話的人會完全沒有等待的感覺(可稱為無感等待),但如果等待時間大於或等於1.5秒,打電話的人就會感覺不耐煩(可稱為不耐等待)。某公司交換機的等待時間與相對次數如下圖。圖中最短等待時間為0.1秒,最長的等待時間為2.0秒,等待時間皆以0.1秒單位計,圖中的黑點代表該等待時間的相對次數,如:等待時間為1.1秒的相對次數為12%。根據上述資訊,試選出正確的選項。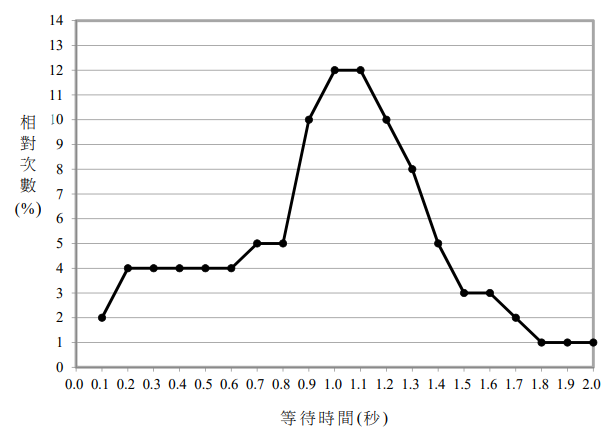
(1) 無感等待所占比例較不耐等待高
(2) 無感等待所占比例達三分之一以上
(3) 發生不耐等待的比例達10%以上
(4) 等待時間不到1.0秒所占比例達一半以上
(5) 等待時間既非無感等待,也未發生不耐等待所占比例達一半以上
109指考數學乙(補考)試題-06
某甲在坐標平面上點 (3,4) 的位置,撇一均勻銅板,若出現正面,則以向量 (1,-1) 的方向與大小移動;若出現反面,則以向量 (-1,-1) 的方向與大小移動。到達新位置之後,重複同樣的步驟,直到抵達 x 軸或 y 軸時停止。試選出正確的選項。
(1) 甲可能到達點 (0,0)
(2) 若甲停在 y 軸,則甲恰好移動 4 次
(3) 甲最後停在 y 軸的機率大於停在 x 軸的機率
(4) 甲最後停在點 (2,0) 的機率為 0
(5) 甲最後停在點 (1,0) 與停在點 (5,0) 的機率相等
109指考數學乙(補考)試題-_A
若 \( f(x) \) 為二次的實係數多項式函數,且滿足 \( f(0)+f(1)=5 \),\( f(1)+f(2)=17 \),\( f(2)+f(0)=14 \),則 \( f(x)=\underline{\quad }x^2+\underline{\quad }x+9 \)
109指考數學乙(補考)試題-_B
坐標平面上有不共線的三點 \( A,B,C \) 且點 \( P \) 在線段 \( BC \) 上,並令 \( AP=xAB+yAC \)。若 \( BP=\frac{1}{2}CP \),則 \( x \) 的值為 \(\underline{\quad }\),\( y \) 的值為 \(\underline{\quad }\)。(化為最簡分數)
109指考數學乙(補考)試題-_C
某實驗室有輻射外洩,危害附近環境。根據調查:該輻射第一天汙染區域是一個以實驗室為中心,半徑2公里的圓形區域,如圖中最內圓的圓內區域。第二天與第三天汙染區域逐漸擴大,都是以實驗室為中心,但汙染半徑越來越大的圓形區域,如圖中第二個與第三個同心圓的圓內區域。已知輻射每天汙染區域依照上述同心圓的模式向外擴大區域,而且新增汙染區域之面積都是前一天新增汙染區域面積的 \( \frac{5}{7} \) 倍,在汙染一直持續下去的條件下,全部汙染區域會趨近於半徑為 \( \sqrt{14 \times 13} \) 公里的圓形區域。
第一天新增面積:\( \pi(2)^2=4\pi \)
第二天新增面積:\( 4\pi\times\frac{5}{7} \)
第三天新增面積:\( 4\pi\times(\frac{5}{7})^2 \)
總面積 = \( 4\pi[1+\frac{5}{7}+(\frac{5}{7})^2+\cdots] = 4\pi\times\frac{1}{1-\frac{5}{7}} = 4\pi\times\frac{7}{2} = 14\pi \)
設半徑為 \( R \),則 \( \pi R^2=14\pi \) ⇒ \( R=\sqrt{14} \)
答案:\( \sqrt{14} \) 報錯
ChatGPT DeepSeek
109指考數學乙(補考)試題-_D
在所有滿足不等式 \( |4-3x|<11 \) 的整數中,選取三相異整數(不計順序),而所選取的三數之中位數大於或等於該三數之平均數的選法有 \( \boxed{16} \boxed{17} \) 種。

