〈107指考數甲〉彙整頁面 - 第 2 頁，總計 2 頁

107指考數學甲試題–C

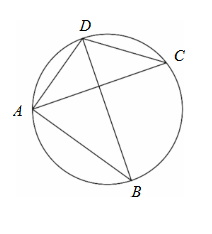
設\(AB\)，\(CD\)為圓上的相異四點。已知圓的半徑為\(\frac{7}{2}\)，\(\overline{AB}=5\)，兩線段\(\overline{AC}\)與\(\overline{BD}\)互相垂直，如圖所示(此為示意圖，非依實際比例)。則\(\overline{CD}\)的長度为\(\sqrt{(\quad)}\)。(化成最簡根式)

答案

设圆的圆心为\(O\)，半径\(r = \frac{7}{2}\)。
作\(OM\perp AB\)于\(M\)，根据垂径定理，\(AM=\frac{AB}{2}=\frac{5}{2}\)。
在\(Rt\triangle OMA\)中，由勾股定理可得\(OM=\sqrt{r^{2}-AM^{2}}=\sqrt{(\frac{7}{2})^{2}-(\frac{5}{2})^{2}}=\sqrt{\frac{49 - 25}{4}}=\sqrt{6}\)。
因为\(AC\perp BD\)，设\(AC\)与\(BD\)相交于点\(P\)，根据圆的性质，\(OM^{2}+ON^{2}=OP^{2}\)（\(ON\)为\(O\)到\(CD\)的距离）。
又因为圆的对称性，可推出\(AB^{2}+CD^{2}=4r^{2}\)（这是圆中两垂直弦的一个性质，可通过勾股定理多次推导得出）。
将\(r = \frac{7}{2}\)，\(AB = 5\)代入可得\(25+CD^{2}=4\times(\frac{7}{2})^{2}\)
\(25+CD^{2}=4\times\frac{49}{4}\)
\(CD^{2}=49 - 25 = 24\)
所以\(CD=\sqrt{24}=2\sqrt{6}\)，故答案为\(24\)。報錯
 ChatGPT DeepSeek

加最愛

107指考數學甲試題-1)

坐標空間中有一個正立方體ABCDEFGH ，試證明A點到平面BDE的距離是對角線AG長度的三分之一。(4分)

答案

設正立方體的稜長為a。
以A為原點，分別以AB、AD、AE所在直線為x、y、z軸建立空間直角坐標系。
則A(0,0,0)，B(a,0,0)，D(0,a,0)，E(0,0,a)，G(a,a,a)。
可求得平面BDE的法向量\(\overrightarrow{n}\)：
\(\overrightarrow{BD}=(-a,a,0)\)，\(\overrightarrow{BE}=(-a,0,a)\)。
設\(\overrightarrow{n}=(x,y,z)\)，由\(\overrightarrow{n}\cdot\overrightarrow{BD}=0\)且\(\overrightarrow{n}\cdot\overrightarrow{BE}=0\)，可得\(\begin{cases}-ax + ay = 0\\-ax + az = 0\end{cases}\)，令x = 1，解得y = 1，z = 1，所以\(\overrightarrow{n}=(1,1,1)\)。
\(\overrightarrow{AG}=(a,a,a)\)，\(\vert\overrightarrow{AG}\vert=\sqrt{a^{2}+a^{2}+a^{2}}=\sqrt{3}a\)。
A點到平面BDE的距離\(d=\frac{\vert\overrightarrow{AB}\cdot\overrightarrow{n}\vert}{\vert\overrightarrow{n}\vert}\)，\(\overrightarrow{AB}=(a,0,0)\)，則\(d=\frac{\vert a\times1 + 0\times1 + 0\times1\vert}{\sqrt{1^{2}+1^{2}+1^{2}}}=\frac{a}{\sqrt{3}}\)。
所以A點到平面BDE的距離\(d=\frac{1}{3}\vert\overrightarrow{AG}\vert\)，即A點到平面BDE的距離是對角線AG長度的三分之一。報錯
 ChatGPT DeepSeek

加最愛

107指考數學甲試題-2)

坐標空間中有一個正立方體ABCDEFGH ，試證明向量\(\overrightarrow{AG}\)與平面BDE垂直。(2分)

答案

由(1)已求得平面BDE的法向量\(\overrightarrow{n}=(1,1,1)\)，且\(\overrightarrow{AG}=(a,a,a)\)。
可發現\(\overrightarrow{AG}=a(1,1,1)=a\overrightarrow{n}\)，即\(\overrightarrow{AG}\)與平面BDE的法向量\(\overrightarrow{n}\)平行。
根據向量與平面垂直的判定，如果一個向量與一個平面的法向量平行，那麼這個向量與該平面垂直。
所以向量\(\overrightarrow{AG}\)與平面BDE垂直。報錯
 ChatGPT DeepSeek

加最愛

107指考數學甲試題-3)

坐標空間中有一個正立方體ABCDEFGH ，如果知道平面BDE的方程式為2x + 2y – z = -7，且A點坐標為(2,2,6)，試求出A點到平面BDE的距離。(2分)

答案

根據點\((x_0,y_0,z_0)\)到平面Ax + By + Cz + D = 0的距離公式\(d=\frac{\vert Ax_0 + By_0 + Cz_0 + D\vert}{\sqrt{A^{2}+B^{2}+C^{2}}}\)。
對於平面2x + 2y - z = -7，即2x + 2y - z + 7 = 0，A(2,2,6)。
則A點到平面BDE的距離\(d=\frac{\vert2\times2 + 2\times2 - 6 + 7\vert}{\sqrt{2^{2}+2^{2}+(-1)^{2}}}=\frac{\vert4 + 4 - 6 + 7\vert}{\sqrt{4 + 4 + 1}}=\frac{9}{3}=3\)。報錯
 ChatGPT DeepSeek

加最愛

107指考數學甲試題-4)

坐標空間中有一個正立方體ABCDEFGH ，承(3)，試求出G點的坐標。(4分)

答案

由(2)知\(\overrightarrow{AG}\)與平面BDE垂直，所以\(\overrightarrow{AG}\)平行於平面BDE的法向量\(\overrightarrow{n}=(2,2,-1)\)（平面2x + 2y - z = -7的法向量）。
設G點坐標為\((x,y,z)\)，則\(\overrightarrow{AG}=(x - 2,y - 2,z - 6)\)。
因為\(\overrightarrow{AG}\)與\(\overrightarrow{n}=(2,2,-1)\)平行，所以\(\frac{x - 2}{2}=\frac{y - 2}{2}=\frac{z - 6}{-1}=k\)（k為常數），即\(x = 2k + 2\)，\(y = 2k + 2\)，\(z = -k + 6\)。
又由(3)知A點到平面BDE的距離是3，且G點到平面BDE的距離與A點到平面BDE的距離相等（正立方體性質）。
將G點坐標\((2k + 2,2k + 2,-k + 6)\)代入點到平面的距離公式\(d=\frac{\vert2(2k + 2)+2(2k + 2)-(-k + 6)+7\vert}{\sqrt{2^{2}+2^{2}+(-1)^{2}}}=3\)。
\(\frac{\vert4k + 4 + 4k + 4 + k - 6 + 7\vert}{3}=3\)，\(\vert9k + 9\vert = 9\)，即\(9k + 9 = 9\)或\(9k + 9 = -9\)。
解得\(k = 0\)或\(k = -2\)，\(k = 0\)時不滿足G與A不重合，所以\(k = -2\)。
則\(x = 2\times(-2)+2=-2\)，\(y = 2\times(-2)+2=-2\)，\(z = -(-2)+6 = 8\)。
所以G點坐標為(-2,-2,8)。報錯
 ChatGPT DeepSeek