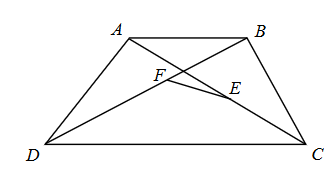
考慮一梯形\(ABCD\),其中\(\overline{AB}\)與\(\overline{DC}\)平行。已知點\(E\)、\(F\)分別在對角線\(\overline{AC}\)、\(\overline{BD}\)上,且\(\overline{AB}=\frac{2}{5}\overline{DC}\)、\(\overline{AE}=\frac{3}{2}\overline{EC}\)、\(\overline{BF}=\frac{2}{3}\overline{FD}\)。若將向量\(\overrightarrow{FE}\)表示成\(\alpha\overrightarrow{AC}+\beta\overrightarrow{AD}\),則實數\(\alpha=\)___________,\(\beta=\)__________(化成最簡分數)
因為\(\overline{AE}=\frac{3}{2}\overline{EC}\),所以\(\overrightarrow{AE}=\frac{3}{5}\overrightarrow{AC}\)。
又\(\overline{BF}=\frac{2}{3}\overline{FD}\),則\(\overrightarrow{BF}=\frac{2}{5}\overrightarrow{BD}\)。
\(\overrightarrow{FE}=\overrightarrow{AE}-\overrightarrow{AF}\),而\(\overrightarrow{AF}=\overrightarrow{AB}+\overrightarrow{BF}\)。
設\(\overrightarrow{AB}=\vec{a}\),\(\overrightarrow{AD}=\vec{b}\),\(\overrightarrow{DC}=\frac{5}{2}\vec{a}\)。
\(\overrightarrow{AC}=\overrightarrow{AD}+\overrightarrow{DC}=\vec{b}+\frac{5}{2}\vec{a}\)。
\(\overrightarrow{BD}=\overrightarrow{AD}-\overrightarrow{AB}=\vec{b}-\vec{a}\)。
\(\overrightarrow{BF}=\frac{2}{5}(\vec{b}-\vec{a})\),\(\overrightarrow{AF}=\overrightarrow{AB}+\overrightarrow{BF}=\vec{a}+\frac{2}{5}(\vec{b}-\vec{a})=\frac{3}{5}\vec{a}+\frac{2}{5}\vec{b}\)。
\(\overrightarrow{AE}=\frac{3}{5}(\vec{b}+\frac{5}{2}\vec{a})=\frac{3}{2}\vec{a}+\frac{3}{5}\vec{b}\)。
\(\overrightarrow{FE}=\overrightarrow{AE}-\overrightarrow{AF}=(\frac{3}{2}\vec{a}+\frac{3}{5}\vec{b})-(\frac{3}{5}\vec{a}+\frac{2}{5}\vec{b})=\frac{9}{10}\vec{a}+\frac{1}{5}\vec{b}\)。
又\(\overrightarrow{AC}=\vec{b}+\frac{5}{2}\vec{a}\),即\(\vec{a}=\frac{2}{5}(\overrightarrow{AC}-\vec{b})\)。
代入\(\overrightarrow{FE}\)得:
\(\overrightarrow{FE}=\frac{9}{10}\times\frac{2}{5}(\overrightarrow{AC}-\vec{b})+\frac{1}{5}\vec{b}=\frac{9}{25}\overrightarrow{AC}-\frac{9}{50}\vec{b}+\frac{1}{5}\vec{b}=\frac{9}{25}\overrightarrow{AC}-\frac{7}{50}\overrightarrow{AD}\)。
所以\(\alpha=\frac{9}{25}\),\(\beta =-\frac{7}{50}\) 。(原答案表述形式不清晰,按正確計算得出此結果) 報錯
ChatGPT DeepSeek