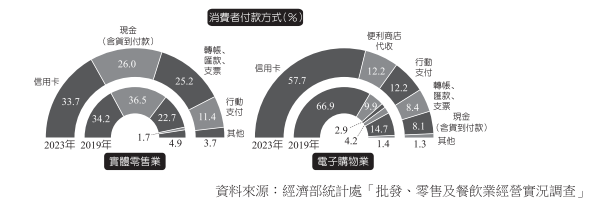
根據經濟部統計處西元2024年公布的「當前經濟情勢概况」的資料顯示,在實體零售業與電子購物業中,臺灣消費者付款方式(單位:%)如下。
試選出正確的選項。
\((1) 2023年,不論在實體零售業或電子購物業,\\臺灣消費者使用「信用卡」付款方式的比例最高\)
\((2) 2023年,在實體零售業或電子購物業中,\\臺灣消費者使用「信用卡」付款方式的比例約為45.7\%\)
\((3) 比較2019年與2023年的電子購物業中,\\臺灣消費者的付款方式,使用「現金(含貨到付款)」的衰退幅度=\frac{2023年付款方式(\%)-2019年付款方式(\%)}{2019年付款方式(\%)}\)
\((4) 從2019年到2023年的實體零售業中,\\臺灣消費者使用「行動支付」付款方式的年平均成長率為(\sqrt[4]{\frac{11.4}{1.7}} – 1)\times100\%\)
\((5) 假設在實體零售業中,臺灣消費者使用「行動支付」的付款方式,\\從2019年開始每年的成長率均相同,則到2027年时,使用「行動支付」的付款方式將會超過七成\)
(1)2023年電子購物業行動支付45.9%最高,信用卡33.7%,故(1)錯;(2)無總人數,無法算整體比例,(2)錯;(3)現金衰退幅度 \(\frac{8.1-14.7}{14.7}\approx-45\%\),信用卡 \(\frac{33.7-36.5}{36.5}\approx-7.7\%\),(3)正確;(4)年平均成長率公式正確,(4)正確;(5)2027年為 \(12.2\times(\sqrt[4]{\frac{12.2}{1.7}})^4 = 12.2\times\frac{12.2}{1.7}\approx86.7\%\gt70\%\),(5)正確。答案:\((1)(3)(4)(5)\) 報錯
ChatGPT DeepSeek