設f(x)為實係數三次多項式,y=f(x)在x=-3有極小值,x=1有極大值,下列關於\(f”(-3)\)和\(f”(1)\)的敘述,正確的選項?
(1) \(f”(-3)=f”(1)=0\)
(2) \(f”(-3)>0\)且\(f”(1)>0\)
(3) \(f”(-3)>0\)且\(f”(1)<0\)
(4) \(f”(-3)<0\)且\(f''(1)>0\)
(5) \(f”(-3)<0\)且\(f''(1)<0\)
數學
114分科測驗數學乙考科試卷-16
某人想在農地種植甲、乙兩種水果,並設定甲水果的種植面積(甲面積)、乙水果的種植面積(乙面積)符合以下三個條件:
(一)甲面積不超過 $15$ 公畝。
(二)甲面積與乙面積的和不超過 $24$ 公畝。
(三)甲面積不超過乙面積的 3 倍,且乙面積不超過甲面積的 2 倍。設甲面積為 $x$ 公畝、乙面積為 $y$ 公畝。根據上述,試回答下列問題。
16. 試問下列哪一個選項的數對 \((x, y)\) 會滿足上述的三個條件?(單選題,3 分)
(1) $(7,15)$
(2) $(12,13)$
(3) $(14,10)$
(4) $(15,4)$
(5) $(16,8)$
114分科測驗數學乙考科試卷-17
承16題,將三個條件以二元一次聯立不等式表示。
17. 試將某人對甲面積、乙面積所設定的三個條件,以 \(x\)、\(y\) 的二元一次聯立不等式表示。(非選擇題,4 分)
114分科測驗數學乙考科試卷-18
18. 已知某人的農地收成時,甲水果每公畝可獲利 6 萬元、乙水果每公畝可獲利 7 萬元。
試 求 某 人 種 植 甲 、 乙 兩 種 水 果 的 最 大 獲 利 為 多 少 萬 元 ? 在 答 題 卷 求 解 區 寫 出
計 算 過 程,並 在 答 題 卷 作 圖 區 畫 出 可 行 解 區 域 及 標 出 其 所 有 頂 點 坐 標,且 以 斜 線
標 示 該 區 域 。( 非 選 擇 題 , 8 分 )
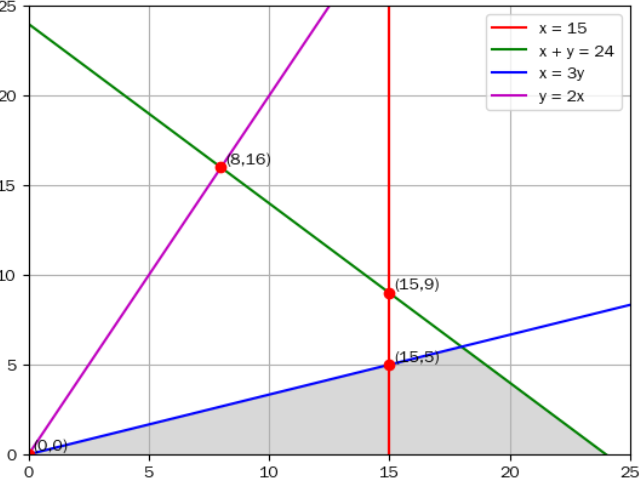
好的,我們先列出所有條件,再用線性規劃求解。
---
## **1. 列出限制條件**
題目給定:
1. \( x \le 15 \)
2. \( x + y \le 24 \)
3. \( x \le 3y \) 且 \( y \le 2x \)
4. \( x \ge 0, \quad y \ge 0 \) (面積不能為負)
---
## **2. 化簡條件 3**
條件 3 拆開:
\[
x \le 3y \quad \Rightarrow \quad y \ge \frac{x}{3}
\]
\[
y \le 2x
\]
所以:
\[
\frac{x}{3} \le y \le 2x
\]
---
## **3. 聯立所有條件**
我們有:
\[
\begin{cases}
0 \le x \le 15 \\
x + y \le 24 \\
y \ge \frac{x}{3} \\
y \le 2x
\end{cases}
\]
---
## **4. 找可行解區域的頂點**
**(1) 交點 \(x=15\) 與 \(x+y=24\)**
\(y = 9\)
檢查 \(y \ge \frac{15}{3} = 5\) ✅
檢查 \(y \le 2\times 15 = 30\) ✅
⇒ 頂點 \(A = (15, 9)\)
**(2) 交點 \(x=15\) 與 \(y=2x\)**
\(y = 30\),但 \(x+y = 45 > 24\) 不行,所以此點不在 \(x+y \le 24\) 內,不考慮。
**(3) 交點 \(x+y=24\) 與 \(y=2x\)**
代入:\(x + 2x = 24 \Rightarrow 3x = 24 \Rightarrow x=8, y=16\)
檢查 \(x \le 15\) ✅
檢查 \(y \ge \frac{8}{3} \approx 2.67\) ✅
⇒ 頂點 \(B = (8, 16)\)
**(4) 交點 \(x+y=24\) 與 \(y = \frac{x}{3}\)**
代入:\(x + \frac{x}{3} = 24 \Rightarrow \frac{4x}{3} = 24 \Rightarrow x = 18\)
但 \(x=18 > 15\),所以此交點不在 \(x \le 15\) 內,不考慮。
**(5) 交點 \(x=15\) 與 \(y = \frac{x}{3}\)**
\(y = 5\),檢查 \(x+y = 20 \le 24\) ✅
⇒ 頂點 \(C = (15, 5)\)
**(6) 交點 \(y = \frac{x}{3}\) 與 \(y = 2x\)**
只有 \(x=0, y=0\),但那是原點 \(O=(0,0)\)。
**(7) 交點 \(y=2x\) 與 \(x=0\)**
\( (0,0) \) 重複。
**(8) 交點 \(x=0\) 與 \(y=0\)** 原點。
但原點利潤最低,顯然不是最大。
---
我們還要檢查 \(x+y=24\) 與 \(x=15\) 之間是否還有其他頂點受 \(y \ge x/3\) 與 \(y \le 2x\) 限制。
實際上,在 \(x=15\) 時,\(y\) 範圍是 \(5 \le y \le 9\)(因為 \(x+y \le 24 \Rightarrow y \le 9\),且 \(y \ge 5\) 來自 \(y \ge x/3\))。
所以 \(x=15\) 邊上兩個端點:\((15,5)\) 和 \((15,9)\) 已取。
在 \(x<15\) 時,最大 \(y\) 受 \(x+y=24\) 與 \(y \le 2x\) 限制,交點是 \(B=(8,16)\)。
檢查 \(y \ge x/3\):\(16 \ge 8/3\) ✅。
---
所以主要頂點為:
\[
O=(0,0), \quad C=(15,5), \quad A=(15,9), \quad B=(8,16)
\]
---
## **5. 目標函數**
利潤:
\[
P = 6x + 7y \ (\text{萬元})
\]
代入:
- \(O\): \(P=0\)
- \(C=(15,5)\): \(P=6\times 15 + 7\times 5 = 90+35=125\)
- \(A=(15,9)\): \(P=90+63=153\)
- \(B=(8,16)\): \(P=48+112=160\)
最大利潤在 \(B=(8,16)\),\(P=160\) 萬元。
---
## **6. 檢查是否還有更大點**
在 \(x+y=24\) 上,\(y=24-x\),
\(P=6x+7(24-x) = 168 - x\),隨 \(x\) 減小而增大,但必須滿足 \(y \le 2x \Rightarrow 24-x \le 2x \Rightarrow 24 \le 3x \Rightarrow x \ge 8\),
且 \(y \ge x/3 \Rightarrow 24-x \ge x/3 \Rightarrow 72-3x \ge x \Rightarrow 72 \ge 4x \Rightarrow x \le 18\)(但 \(x \le 15\) 更嚴格)。
所以 \(x\) 範圍 \(8 \le x \le 15\) 在 \(x+y=24\) 上。
\(P=168-x\) 在 \(x=8\) 最大 \(160\),在 \(x=15\) 時 \(153\)。
所以 \(B\) 點確實最大。
---
**最終答案:**
\[
\boxed{160}
\]
最大利潤 160 萬元,此時 \(x=8\) 公畝,\(y=16\) 公畝。 報錯
ChatGPT DeepSeek
114分科測驗數學甲試卷-01
坐標平面上,函數 \(y=\sin x\) 的圖形關於 \(x=\frac{\pi}{2}\) 對稱,如圖所示。試求出在 \(0<\theta \leq\pi\) 的範圍中滿足 \(\sin \theta=\sin \left(\theta+\frac{\pi}{5}\right)\) 的 \(\theta\) 值?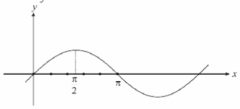
\((1) \frac{\pi}{5}\)
\((2) \frac{2\pi}{5}\)
\((3) \frac{3\pi}{5}\)
\((4) \frac{4\pi}{5}\)
\((5) \pi\)
1. 由 \(\sin \theta = \sin \left(\theta+\frac{\pi}{5}\right)\),依性質:\(\sin A = \sin B\) 則 \(A = B + 2k\pi\) 或 \(A = \pi - B + 2k\pi\)(\(k\in\mathbb{Z}\));
2. 前者得 \(\frac{\pi}{5}=2k\pi\),無解;後者得 \(2\theta = \frac{4\pi}{5}+2k\pi\),即 \(\theta = \frac{2\pi}{5}+k\pi\);
3. 結合 \(0<\theta \leq\pi\),僅 \(k=0\) 時 \(\theta=\frac{2\pi}{5}\) 符合。答案:(2) \(\frac{2\pi}{5}\)","是 報錯
ChatGPT DeepSeek
114分科測驗數學甲試卷-02
114分科測驗數學甲試卷-03
《幾何原本》云:「給定相異兩點可決定一條直線」。相異三點共線僅決定1條直線。坐標平面上,圓 \(\Gamma_1: x^2+y^2=4\) 與兩坐標軸交於4點、圓 \(\Gamma_2: x^2+y^2=2\) 與直線 \(x-y=0\) 交於2點、與直線 \(x+y=0\) 交於2點。試問這8點共可決定幾條不同的直線?
(1) 12
(2) 16
(3) 20
(4) 24
(5) 28
114分科測驗數學甲試卷-04
試從下列坐標平面上的二次曲線中,選出與所有的鉛直線都相交的選項?
(1) \(\frac{x^2}{9}+\frac{y^2}{4}=1\)
(2) \(\frac{x^2}{9}-\frac{y^2}{4}=1\)
(3) \(-\frac{x^2}{9}+\frac{y^2}{4}=1\)
(4) \(y=\frac{4}{9}x^2\)
(5) \(x=\frac{4}{9}y^2\)
1. 鉛直線為 \(x=a\)(\(a\) 為任意實數),代入曲線方程看是否有解;
2. (1)橢圓:\(x=a\) 代入得 \(y^2=4(1-\frac{a^2}{9})\),\(|a|>3\) 時無解,不選;
3. (2)雙曲線:\(x=a\) 代入得 \(y^2=4(\frac{a^2}{9}-1)\),\(|a|<3\) 時無解,不選;
4. (3)雙曲線:\(x=a\) 代入得 \(y^2=4(\frac{a^2}{9}+1)\),恆有解,選;
5. (4)拋物線:\(x=a\) 代入得 \(y=\frac{4}{9}a^2\),恆有解,選;
6. (5)拋物線:\(x=a\) 代入得 \(y^=\frac{9a}{4}\),\(a<0\) 時無解,不選。答案:(3)(4) 報錯
ChatGPT DeepSeek