數學模考
113學測數學B1模考4-02
若現在時間為中午 12 點整,經過若干時間後,時鐘上的時針與分針將第一次重疊在一起,試問此時時針與中午 12 點時的時針,所夾之銳角 \(\theta\) 為多少弧度?
(1) \(\frac{1}{7}\pi\)
(2) \(\frac{1}{6}\pi\)
(3) \(\frac{2}{11}\pi\)
(4) \(\frac{2}{9}\pi\)
(5) \(\frac{1}{5}\pi\)
113學測數學B1模考4-03
試問當 \(-2\pi \leq x \leq 2\pi\) 時,有多少個實數 \(x\) 滿足方程式 \(\sin 3x = 3\sin x\)(已知當 \(0 \lt x \lt \frac{\pi}{6}\) 時,無實數解)。
(1) 3
(2) 5
(3) 7
(4) 9
(5) 10 個以上
113學測數學B1模考4-04
設 x 與 y 的關係式為 \(y = 8\log \left( \frac{x}{3} \right)^2\),且當 \(x = x_1, x_2\) 時,其對應的 y 值分別為 \(y_1, y_2\),其中 \(x_1, x_2\) 為正實數,若 \(x_2 = 9x_1\),則對於 \(y_1, y_2\) 的關係,試選出正確的選項。
(1) \(y_2 = 9y_1\)
(2) \(y_2 = 8\log \left( 9y_1 \right)\)
(3) \(y_2 = 8y_1 – 2\log 3\)
(4) \(y_2 = y_1 + 32\log 3\)
(5) \(y_2 = y_1 + 2\log 3\)
113學測數學B1模考4-05
臺灣大約位於東經 120 度北緯 24 度,而在同緯度的地球另一側,即西經 60 度北緯 24 度,恰好為有名的百慕達三角。今有半徑 12 公分的地球儀,令 A 點為東經 120 度北緯 24 度、B 點為西經 60 度北緯 24 度,試問在球面上 A、B 點的最短距離為幾公分?
(1) \(\frac{44}{5}\pi\)
(2) \(12\pi \times \cos 24^\circ\)
(3) \(12\pi \times \sin 24^\circ\)
(4) \(12\pi\)
(5) \(24\pi\)
113學測數學B1模考4-06
不等式
\[\begin{cases}
|x – n| \lt a \\
|x – n| \gt b
\end{cases}\]
其中 n 為整數,a、b 為正實數且 $a \gt b$。已知此不等式共有 10 個整數解,試求 a – b 的最大值。
(1) 2
(2) 3
(3) 4
(4) 5
(5) 6
113學測數學B1模考4-07
在物理及化學實驗中,常常對實驗數據進行函數變換,以方便觀察資料的關係。下表中的 X、Y 為原始實驗數據,觀察 Y 的數據後,實驗人員以 Z = \(\log_2 Y\) 進行函數變換,試選出正確的選項。
| X | 1 | 2 | 4 | 8 | 10 |
| Y | \(\sqrt{2}\) | 2 | 4 | 16 | 32 |
(1) X、Y 的相關係數等於 X、Z 的相關係數
(2) X、Z 為完全正相關
(3) 令 Y 的標準差為 \(\sigma_y\),Z 的標準差為 \(\sigma_z\),則 \(\sigma_z = \log_2 \sigma_y\)
(4) X 的標準差 σ_X 為 2 \(\sqrt{3}\)
(5) Z 對 X 的最適直線(迴歸直線)為 \(Z = 0.5X\)
113學測數學B1模考4-08
今三次函數 \(f(x) = x^3 – 2ax^2 + 3ax – a\),一次函數 \(g(x) = b(x-2) + 1\),已知 \(f(x)\) 的圖形對稱中心的 x 坐標為 2,試選出正確的選項。
(1) \(a = 3\)
(2) \(a = -3\)
(3) \(f(x)\) 的圖形對稱中心的 y 坐標為 -1
(4) 當 \(b = 4\) 時,則方程式 \(y = f(x) + g(x)\) 的圖形與 x 軸恰有一個交點
(5) 當 \(b = 1\) 時,則方程式 \(y = f(x) + g(x)\) 的圖形與 x 軸恰有三個交點
113學測數學B1模考4-09
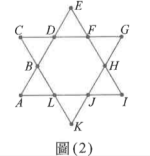 六角星又名大衛之星,為猶太教的標示之一,因其對稱的美感,也經常出現在許多圖騰上,甚至在 1 美元鈔票上也能找到它的蹤影。如圖 (2),此六角星的六個棱角是邊長為 1 的正三角形所組成,中間則是邊長為 1 的正六邊形,試選出正確的選項。
六角星又名大衛之星,為猶太教的標示之一,因其對稱的美感,也經常出現在許多圖騰上,甚至在 1 美元鈔票上也能找到它的蹤影。如圖 (2),此六角星的六個棱角是邊長為 1 的正三角形所組成,中間則是邊長為 1 的正六邊形,試選出正確的選項。
(1) \(\overrightarrow{AF} = \overrightarrow{AE} + \overrightarrow{EF}\)
(2) \(\overrightarrow{AF} = 2\overrightarrow{AB} + \overrightarrow{AL}\)
(3) \(\overrightarrow{AB} \cdot \overrightarrow{AL} = 1\)
(4) \(\overrightarrow{EF} \cdot \overrightarrow{AG} = 0\)
(5) \(\overrightarrow{AF} \cdot \overrightarrow{AG} = 10\)
113學測數學B1模考4-10
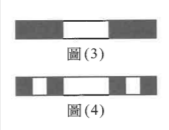 康托爾集(Cantor set)為德國數學家格奧爾格·康托爾引入,由於具有許多特殊性質,為高等數學常見的範例。生成規則如下:
康托爾集(Cantor set)為德國數學家格奧爾格·康托爾引入,由於具有許多特殊性質,為高等數學常見的範例。生成規則如下:
第一步驟從線段 \([0,1]\) 去除中間三分之一,留下 \(\left[ 0, \frac{1}{3} \right] \cup \left[ \frac{2}{3}, 1 \right]\),即圖(3)。
第二步驟再去除所有線段中間三分之一,留下 \(\left[ 0, \frac{1}{9} \right] \cup \left[ \frac{2}{9}, \frac{1}{3} \right] \cup \left[ \frac{2}{3}, \frac{7}{9} \right] \cup \left[ \frac{8}{9}, 1 \right]\),即圖(4)。不斷重複以上步驟。令 \( E_n \) 為經過 \( n \) 次步驟後,其集合中所有線段長的總和,試選出正確的選項。
(1) 經過 3 次步驟後,共有 8 個線段
(2) 經過 5 次步驟後,每段線段長度為 \(\frac{1}{32}\)
(3) \( E_n \) 的遞迴關係式為
\(\begin{cases}
E_1 = \frac{2}{3} \\
E_n = \frac{2}{3} E_{n-1} ,當 n \geq 2 \\
\end{cases}\)
(4) 當 \( n \geq 6 \) 時,\( E_n \lt \frac{1}{10} \),其中 \( n \) 為正整數
(5) \( E_1 + E_2 + E_3 + E_4 + E_5 = \frac{211}{81} \)