〈104以前學測數學〉彙整頁面 - 第 7 頁，總計 8 頁

104學測數學考科-01

每週同一時間點記錄某植物的成長高度,連續五週的數據為
$a_1 = 1$, $a_2 = 2$, $a_3 = 6$, $a_4 = 15$, $a_5 = 31$。
請問此成長高度數列滿足下列選項中哪一個式子？
(1) $a_{i+1} = 3a_i – 1$,$i = 1, 2, 3, 4$
(2) $a_i = i!$,$i = 1, 2, 3, 4, 5$
(3) $a_{i+1} = a_i + i^2$,$i = 1, 2, 3, 4$
(4) $a_i = 2^i – 1$,$i = 1, 2, 3, 4, 5$
(5) $a_{i+1} = i a_i + 1$,$i = 1, 2, 3, 4$

[單選]

答案

根據數列數據,$a_{i+1} = a_i + i^2$ 符合數列的變化。因此,正確答案是 (3)。

加最愛

104學測數學考科-02

第 1 天獲得 1 元、第 2 天獲得 2 元、第 3 天獲得 4 元、第 4 天獲得 8 元、依此每天所獲得的錢為前一天的兩倍,如此進行到第 30 天,試問這 30 天所獲得的錢,總數最接近下列哪一個選項？
(1) 10,000 元
(2) 1,000,000 元
(3) 100,000,000 元
(4) 1,000,000,000 元
(5) 1,000,000,000,000 元

[單選]

答案

這是一個等比數列,總和為 $S = 2^{30} - 1$,約為 1,000,000,000 元。因此,正確答案是 (4)。

加最愛

104學測數學考科-03

有兩組供機器運作的配件 $A$、$B$,其單獨發生故障的機率分別為 0.1、0.15。只有當 $A, B$ 都發生故障時,此機器才無法運作。$A$、$B$ 兩配件若用串接方式,前面故障會導致後面故障,但若後面故障則不會影響前面的故障情形；若用並列方式,則故障情形互不影響。若考慮以下三種情形：
(一) 將 $B$ 串接於 $A$ 之後
(二) 將 $A$ 串接於 $B$ 之後
(三) 將 $A, B$ 獨立並列
在情況(一)、(二)、(三)之下,機器無法運作的機率分別為 $p_1$、$p_2$、$p_3$。請選出正確的選項。
(1) $p_1 > p_2 > p_3$
(2) $p_2 > p_1 > p_3$
(3) $p_3 > p_2 > p_1$
(4) $p_3 > p_1 > p_2$
(5) $p_1 = p_2 > p_3$

[單選]

答案

(1) $ A \to B $：$ p_1 = P(A') = 0.1 $

(2) $ B \to A $：$ p_2 = P(B') = 0.15 $

(3) $ A, B $ 獨立：$ p_3 = P(A' \cap B') = P(A') \times P(B') = 0.1 \times 0.15 $

∴ $ p_2 > p_1 > p_3 $

故選 (2)

加最愛

104學測數學考科-04

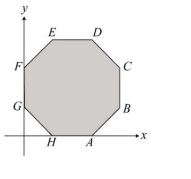
一線性規劃問題的可行解區域為坐標平面上的正八邊形 $ABCDEFGH$ 及其內部,如右圖。已知目標函數 $ax + by + 3$（其中 $a, b$ 為實數）的最大值只發生在 $B$ 點。請問當目標函數改為 $3bx – ay$ 時,最大值會發生在下列哪一點？

(1) $A$
(2) $B$
(3) $C$
(4) $D$
(5) $E$

[單選]

答案

由題意知 $ \overline{AB} $ 之斜率為 1（∵ $ \angle BAH = 135^\circ $）。

∵ 目標函數 $ ax + by + 3 $ 之最大值發生在 $ B $ 點，
∴ 斜率 $ -\dfrac{a}{b} > 1 $，即 $ \dfrac{a}{b} < -1 $（亦即 $ \dfrac{b}{a} > -1 $）。

又目標函數改為 $ 3 - bx - ay $ 時，其斜率為 $ 0 < -\dfrac{b}{a} < 1 $。 ∴ $ 3 - bx - ay $ 之最大值會發生在 $ A $ 點。故選 (1)。

加最愛

104學測數學考科-05

小明參加某次路跑 10 公里組的比賽,下表為小明手錶所記錄之各公里的完成時間、平均心率及步數：
| 完成時間 | 平均心率 | 步數 |
| 5:00 | 161 | 990 |
| 4:50 | 162 | 1000 |
| 4:50 | 165 | 1005 |
| 4:55 | 162 | 995 |
| 4:40 | 171 | 1015 |
| 4:41 | 170 | 1005 |
| 4:35 | 173 | 1050 |
| 4:35 | 181 | 1050 |
| 4:40 | 171 | 1050 |
| 4:34 | 188 | 1100 |
在這 10 公里的比賽過程,請依據上述數據,選出正確的選項。
(1) 由每公里的平均心率得知小明最高心率為 188
(2) 小明此次路跑,每步距離的平均小於 1 公尺
(3) 每公里完成時間和每公里平均心率的相關係數為正相關
(4) 每公里步數和每公里平均心率的相關係數為正相關
(5) 每公里完成時間和每公里步數的相關係數為負相關

[多選]

答案

(1) ×：由圖表可知，平均心率最高為 188，
故小明在第 10 公里的最高心率應大於 188。

(2) ○：平均步數大於 1000 步，因此每步距離的平均小於 1 公尺。

(3) ×：完成每公里的時間愈短，心率愈高，二者為負相關。

(4) ○：每公里步數愈多，心率愈高，二者為正相關。

(5) ○：每公里完成時間愈少，步數愈多，二者為負相關。

故選 (2)(4)(5)。

加最愛

104學測數學考科-06

設 $f(x)$ 是首項係數為 1 的實係數二次多項式。請選出正確的選項。
(1) 若 $f(2) = 0$,則 $x – 2$ 可整除 $f(x)$
(2) 若 $f(2) = 0$,則 $f(x)$ 為整係數多項式
(3) 若 $f(\sqrt{2}) = 0$,則 $f(-\sqrt{2}) = 0$
(4) 若 $f(2i) = 0$,則 $f(-2i) = 0$
(5) 若 $f(2i) = 0$,則 $f(x)$ 為整係數多項式

[多選]

答案

根據多項式的性質：
(1) 若 $f(2) = 0$,則 $x - 2$ 可整除 $f(x)$,正確。
(2) 若 $f(2) = 0$,則 $f(x)$ 不一定為整係數多項式,錯誤。
(3) 若 $f(\sqrt{2}) = 0$,則 $f(-\sqrt{2}) = 0$,錯誤(要有理係數才成立)。
(4) 若 $f(2i) = 0$,則 $f(-2i) = 0$,正確。
(5) 若 $f(2i) = 0$,則 $f(x)$ 為整係數多項式,正確。
因此,正確答案是 (1)(4)(5)。

加最愛

104學測數學考科-07

坐標平面上,在函數圖形 $y = 2^x$ 上,標示 $A$、$B$、$C$、$D$ 四個點,其 $x$ 坐標分別為 $-1$、$0$、$1$、$2$。請選出正確的選項。
(1) 點 $B$ 落在直線 $AC$ 下方
(2) 在直線 $AB$、直線 $BC$、直線 $CD$ 中,以直線 $CD$ 的斜率最大
(3) $A$、$B$、$C$、$D$ 四個點,以點 $B$ 最靠近 $x$ 軸
(4) 直線 $y = 2x$ 與 $y = 2^x$ 的圖形有兩個交點
(5) 點 $A$ 與點 $C$ 對稱於 $y$ 軸

[多選]

答案

根據函數圖形分析：
(1) 點 $B$ 落在直線 $AC$ 下方,正確。
(2) 直線 $CD$ 的斜率最大,正確。
(3) 點 $A$ 最靠近 $x$ 軸,選項錯誤。
(4) 直線 $y = 2x$ 與 $y = 2^x$ 的圖形有兩個交點,正確。
(5) 點 $A$ 與點 $C$ 不對稱於 $y$ 軸,錯誤。
因此,正確答案是 (1)(2)(4)。

加最愛

104學測數學考科-08

坐標平面上有一雙曲線,其漸近線為 $x – y = 0$ 和 $x + y = 0$。關於此雙曲線的性質,請選出正確的選項。
(1) 此雙曲線的方程式為 $\frac{x^2}{r^2} – \frac{y^2}{r^2} = 1$ 或 $\frac{x^2}{r^2} – \frac{y^2}{r^2} = -1$,其中 $r$ 為非零實數
(2) 此雙曲線的實軸長等於共軛軸長
(3) 若點 $(a, b)$ 為此雙曲線在第一象限上一點,則當 $a > 1000$ 時,$|a – b| < 1$
(4) 若點 $(a, b)$、$(a’, b’)$ 為此雙曲線在第一象限上兩點且 $a < a'$,則 $b < b'$
(5) 此雙曲線同時對稱於 $x$ 軸與 $y$ 軸

[多選]

答案

根據雙曲線的性質：
(1) 雙曲線的方程式為 $\frac{x^2}{r^2} - \frac{y^2}{r^2} = 1$ 或 $\frac{x^2}{r^2} - \frac{y^2}{r^2} = -1$,正確。
(2) 實軸長等於共軛軸長,正確。
(3) 當 $a > 1000$ 時,$|a - b| < 1$,選項錯誤($\because a^2-b^2=\pm r^2可令r=999999則b\to0$)。
(4) 若 $a < a'$,則 $b < b'$,選項錯誤。
(5) 雙曲線對稱於 $x$ 軸與 $y$ 軸,正確。
因此,正確答案是 (1)(2)(4)(5)。

加最愛

104學測數學考科-09

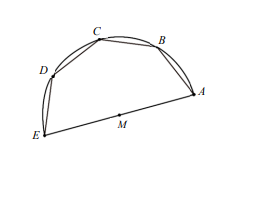
如圖,以 $M$ 為圓心、$MA = 8$ 為半徑畫圓,$AE$ 為該圓的直徑,$B$、$C$、$D$ 三點皆在圓上,且 $AB = BC = CD = DE$。若 $MD = 8(\cos(\theta + 90^\circ), \sin(\theta + 90^\circ))$。請選出正確的選項。

(1) $MA = 8(\cos \theta, \sin \theta)$
(2) $MC = 8(\cos(\theta + 45^\circ), \sin(\theta + 45^\circ))$
(3) （內積）$MA \cdot MA = 8$
(4) （內積）$MB \cdot MD = 0$
(5) $BD = 8(\cos \theta + \cos(\theta + 90^\circ), \sin \theta + \sin(\theta + 90^\circ))$

[多選]

答案

將圖形坐標化，令 $ M(0, 0) $，$ A(8, 0) $。
由題意知 $ B, C, D $ 為弧 $ \overparen{AE} $ 的四等分點，
故 $ D(8\cos 135^\circ, 8\sin 135^\circ) $，即 $ \theta = 45^\circ $。

(1) ×：$ \overrightarrow{MA} = (8, 0) $

(2) ○：$ \overrightarrow{MC} = (0, 8) = (8\cos 90^\circ, 8\sin 90^\circ) $

(3) ×：$ \overrightarrow{MA} \cdot \overrightarrow{MA} = 64 $

(4) ○：$ \overrightarrow{MB} \perp \overrightarrow{MD} \Rightarrow \overrightarrow{MB} \cdot \overrightarrow{MD} = 0 $

(5) ×：$ \overrightarrow{BD} = 8(\cos 135^\circ - \cos 45^\circ, \sin 135^\circ - \sin 45^\circ) $

故選 (2)(4)

加最愛

104學測數學考科-10

某一班共有 45 人,問卷調查有手機與平板電腦的人數。從統計資料顯示此班有 35 人有手機,而有 24 人有平板電腦。設：
$A$ 為同時有手機與平板電腦的人數
$B$ 為有手機,但沒有平板電腦的人數
$C$ 為沒有手機,但有平板電腦的人數
$D$ 為沒有手機,也沒有平板電腦的人數
請選出恆成立的不等式選項。
(1) $A > B$
(2) $A > C$
(3) $B > C$
(4) $B > D$
(5) $C > D$

[多選]

答案

設有手機的集合為 $ H $，$ n(H) = 35 $；
設有平板的集合為 $ P $，$ n(P) = 24 $。

(1) ∵ $ n(H \cup P) \leq 45 $
∴ $ n(H) + n(P) - n(H \cap P) \leq 45 $
⇒ $ n(H \cap P) \geq 35 + 24 - 45 = 14 $
又 $ n(H \cap P) \leq \min(n(H), n(P)) = 24 $
∴ $ n(A) $ 最多 24 人，最少 14 人。

(2) 由 (1) 得 $ n(B) $ 最多 21 人，最少 11 人。

(3) 由 (1) 得 $ n(C) $ 最多 10 人，最少 0 人。

(4) 由 (1)、(2)、(3) 得：
\[
n(D) = n(H' \cap P') = n(H \cup P)'
= 45 - n(H \cup P)
= 45 - [n(H) + n(P) - n(H \cap P)]
= n(H \cap P) - 14
\]
∴ $ n(D) $ 最多 10 人，最少 0 人。

故選 (2)(3)(4)。

加最愛

Saved articles