畫家把空間景物用單點透視法畫在平面的畫紙上時,有以下原則要遵守:一、空間中的直線畫在畫紙上必須是一條直線。二、空間直線上點的相關位置必須和畫紙所畫的點的相關位置一致。三、 空間 直 線上 的 任四個 相 異點的\(K\)值, 和畫 紙所畫 的四 個 點之\(K\)值 必 須相 同,其 中\(K\)值的定義如下:直線上任給四個有順序的相異點\(P_1\), \(P_2\), \(P_3\), \(P_4\) ,如下圖。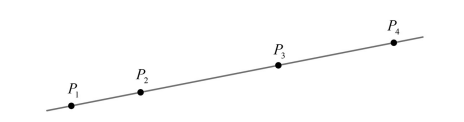 其所對應的\(K\)值定義為\[K=\frac{\overline{P_1P_4}\times \overline{P_2P_3}}{\overline{P_1P_3}\times \overline{P_2P_4}}\] 。今 某 畫家 依 照 以上 原 則, 將 空 間 中 一 直線 及 該 線 上的 四 相 異點\(Q_1\), \(Q_2\), \(Q_3\), \(Q_4\) 描 繪 在 畫 紙上,其中\(Q_1Q_2 = Q_2Q_3 = Q_3Q_4\) 。若將畫紙上所畫的直線視為一數線,並將線上的點用坐標來表示,則在下列選項的四個坐標中,試問哪一組最可能是該四點在畫紙上的坐標?
其所對應的\(K\)值定義為\[K=\frac{\overline{P_1P_4}\times \overline{P_2P_3}}{\overline{P_1P_3}\times \overline{P_2P_4}}\] 。今 某 畫家 依 照 以上 原 則, 將 空 間 中 一 直線 及 該 線 上的 四 相 異點\(Q_1\), \(Q_2\), \(Q_3\), \(Q_4\) 描 繪 在 畫 紙上,其中\(Q_1Q_2 = Q_2Q_3 = Q_3Q_4\) 。若將畫紙上所畫的直線視為一數線,並將線上的點用坐標來表示,則在下列選項的四個坐標中,試問哪一組最可能是該四點在畫紙上的坐標?
(1) \(1, 2, 4, 8\);
(2) \(3, 4, 6, 9\);
(3) \(1, 5, 8, 9\);
(4) \(1, 2, 4, 9\);
(5) \(1, 7, 9, 10\)
[單選]
答案
$\begin{align*}
&定義交比K=\frac{3t×t}{2t×2t}=\frac{3}{4},逐一計算選項:\\
&(1) K=\frac{7×2}{3×6}=\frac{7}{9};\\
&(2) K=\frac{6×2}{3×5}=\frac{4}{5};\\
&(3) K=\frac{8×3}{7×4}=\frac{6}{7};\\
&(4) K=\frac{8×2}{3×7}=\frac{16}{21};\\
&(5) K=\frac{9×2}{8×3}=\frac{3}{4};\\
\\
&故選(5)。
\end{align*}$
https://www.ceec.edu.tw/files/file_pool/1/0m053363176747148935/04-111%e5%ad%b8%e6%b8%ac%e6%95%b8%e5%ad%b8b%e9%81%b8%e6%93%87%28%e5%a1%ab%29%e9%a1%8c%e7%ad%94%e6%a1%88.pdf

