在坐標平面上,設向量 \(\vec{a} = (k+1,4)\),向量 \(\vec{b} = (1,k-2)\),試選出正確的選項。
(1)當 \(k=0\) 時,對任意向量 \(\vec{c}\),可以找到數對 \((x,y)\) 使得 \(\vec{c} = x\vec{a} + y\vec{b}\)
(2)當 \(k=3\) 時,對任意向量 \(\vec{c}\),無法找到數對 \((x,y)\) 使得 \(\vec{c} = x\vec{a} + y\vec{b}\)
(3)當 \(\vec{c} = (3,2)\) 時,對任意實數 \(k\),至多找到一組數對 \((x,y)\) 使得 \(\vec{c} = x\vec{a} + y\vec{b}\)
(4)當 \(\vec{c} = (1,-4)\) 時,對任意實數 \(k\),至多找到一組數對 \((x,y)\) 使得 \(\vec{c} = x\vec{a} + y\vec{b}\)
(5)可找到實數 \(k\),使得 \(\left|\begin{array}{ccc}k+1 & 1 \\ 4 & k-2\end{array}\right| = -\begin{array}{ccc}|\vec{a}| |\vec{b}|\end{array}\)
數學模考
113學測數學A1模考4-12
 在坐標平面上,\(O(0,0)\) 為原點,\(A(0,-1)\) 為單位圓上一點,試選出正確的選項。
在坐標平面上,\(O(0,0)\) 為原點,\(A(0,-1)\) 為單位圓上一點,試選出正確的選項。
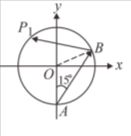
(1)一質點由點 A 且沿著與 y 軸正向夾角為 15°的方向直線前進,經點 B 反射(即 \(\angle OBA = \angle OBP_1\))至圓上的點$ P_1$,再反射至圓上的點 $P_2$,如圖所示。如此連續進行 $n$ 次反射後會到圓上的點 $P_n$,則點 $P_{114}$ 的坐標為 \(\left(\frac{1}{2}, -\frac{\sqrt{3}}{2}\right)\)
(2)設 $n$ 為正整數,若點 $A$ 經矩陣 \(J = \left[\begin{array}{ccc}1 & 2 \\ 2 & -1\end{array}\right]\) 連續作線性變換 $n$ 次的對應點為 \(Q_n\left(x_n, y_n\right)\),即\(J^n \left[\begin{array}{c}0 \\ -1\end{array}\right] = \left[\begin{array}{c}x_n \\ y_n\end{array}\right]\),則滿足 \(Q_n Q_{n+1} \gt 2025\) 的最小正整數 $n$ 為 $8$
(3)設矩陣\(M_k = \begin{bmatrix}\cos \frac{k\pi}{180} & -\sin \frac{k\pi}{180} \\ \sin \frac{k\pi}{180} & \cos \frac{k\pi}{180}\end{bmatrix}, N_k = \begin{bmatrix}\cos \frac{k\pi}{180} & \sin \frac{k\pi}{180} \\ \sin \frac{k\pi}{180} & -\cos \frac{k\pi}{180}\end{bmatrix}, T = \begin{bmatrix}2 & -1 \\ 1 & 2\end{bmatrix}\)若單位圓上的動點 \( C(a,b) \) 在第一象限且 \(\frac{1}{2} \lt a \lt 1\),點 \( C \) 經矩陣 \( M_1N_2 M_2 N_4 M_3 T \) 作線性變換的對應點為點 \( D \),則點 \( D \) 的坐標可能為 \(\left( -\frac{3}{5}, \frac{4}{5} \right)\)
(4)設 \( J = \begin{bmatrix}1 & 2 \\ 2 & -1\end{bmatrix}, T = \begin{bmatrix}2 & -1 \\ 1 & 2\end{bmatrix}\),若單位圓經矩陣 \( SJT \) 變換後的圖形為 \( \Gamma \),則 \( O \) 點與 \( \Gamma \) 上的點之最長距離與最短距離的和為 $35$
(5)設 \( J = \begin{bmatrix}1 & 2 \\ 2 & -1\end{bmatrix}, T = \begin{bmatrix}2 & -1 \\ 1 & 2\end{bmatrix}, U = \begin{bmatrix}2 & 0 \\ 3 & 2\end{bmatrix}\),若單位圓經矩陣 \( UJT \) 變換後的圖形為 \( \Omega \),則 \( O \) 點與 \( \Omega \) 上的點之最長距離與最短距離的和為 $25$
113學測數學A1模考4-13
已知 \( \vec{a} = (1,2,3), \vec{b} = (-1,1,2), \vec{c} = (3,5,6), \vec{d} = (4,-5,-11) \),若 \( \vec{d} = x\vec{a} + y\vec{b} + z\vec{c} \),則 \( x + y + z = \underline{\phantom{a}} \)。
[選填題]113學測數學A1模考4-14
113學測數學A1模考4-15
小南想要安排七天的運動計畫。他打算安排的運動項目為:桌球、羽球、重訓、大極拳。若他每天只進行一種運動且每種運動要至少進行一次,則他安排運動計畫的方式有 $\underline{\phantom{a}} $種。
[選填題]113學測數學A1模考4-16
在坐標空間中兩向量 \( \overrightarrow{a} = (1,-2,-2) \) 及 \( \overrightarrow{b} \) 滿足 \( \overrightarrow{a} \times \overrightarrow{b} = (0,1,-1) \),已知 \( \overrightarrow{b} = x \overrightarrow{a} + \overrightarrow{c} \),其中 \( \overrightarrow{c} \cdot \overrightarrow{a} = 0 \),且 \( x \) 為實數。若 \( \overrightarrow{c} = (p,q,r) \),則 \( p^2 – q^2 + r^2 \) 之值為$ \underline{\phantom{a}}$。(化成最簡分數)
[選填題]113學測數學A1模考4-17
設點 \( A(x_1, y_1) \) 在 \( y = 2^x \) 的圖形上,點 \( B(x_2, y_2) \) 在 \( y = \log_2 x \) 的圖形上,且 \( A 、 B \) 均在第一象限,若 \( O \) 為坐標平面上的原點,已知 \( OA = OB = 4\sqrt{17} \) 且 \( \cos \angle AOB = \frac{8}{17} \),則 \( \frac{x_1 + 2x_2}{y_1 + 2y_2} \)之值為_。(化成最簡分數)
[選填題]113學測數學A1模考4-18
 以下是針對排球少年裡影山與日向的「怪人快攻」的情報分析:
以下是針對排球少年裡影山與日向的「怪人快攻」的情報分析:
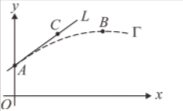
右圖為平面直角坐標系,拋物線$\Gamma$ 為影山托球時,排球 行進的軌跡,從 $A$點開始上升,到最高點 $B$ 點(頂點)時,日向會在該點殺球。如果是「怪人快攻」時,軌跡會變成直 線 $L$ ,從$ A$點上升到$C$ 點時,則日向會改在該點殺球。
[題組:第18題到第20題]設 $A(0,2)$、$B(6,4)$,$\Gamma$會通過$A、B$兩點,若直線 $L$ 為$\Gamma$在 $x=0$ 的一次近似(局部近似)。則直線 $L$ 的斜率為何?(單選題)
(1) $\dfrac{2}{3}$
(2) $\dfrac{3}{4}$
(3) $\dfrac{4}{5}$
(4) $1$
(5) $\dfrac{6}{5}$
113學測數學A1模考4-19
 [題組:第18題到第20題]
[題組:第18題到第20題]
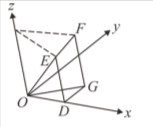
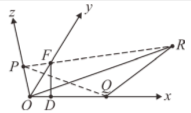
19. 如圖所示,在空間中,日向殺球的擊球點為 \( P \) 點,排球行進的軌跡為直線,排球的落地點均在 \( \overline{QR} \) 上,其中 \( \overline{PQ} \) 為排球行進的最短路徑,\( \overline{PR} \) 為排球行進的最遠路徑,且 \( \overline{PQ} \)、\( \overline{PR} \) 兩線段對 \( xy \) 平面的投影分別
為 \( \overline{OQ} \)、\( \overline{OR} \)。設 \( O(0,0,0) \)、\( P(0,0,4) \)、\( Q(8,0,0) \)、\( R(12,8,0) \),\( \overline{DF} \) 為兩歪斜線 \( \overleftrightarrow{OQ} \) 與 \( \overleftrightarrow{PR} \) 的公垂線段,求 \( F \) 點的坐標為_