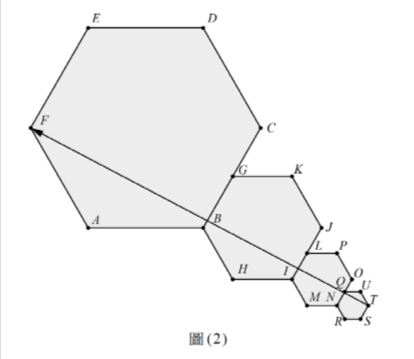
設\(A,B,C\)為圓\(x^2+y^2=4\)上的點，O 為圓心，若\(OA \perp OB\)且內積\(\overset{\rightharpoonup}{OA} \cdot \overset{\rightharpoonup}{OC} \gt \frac{5}{2}\)，則下列哪些選項可能為內積\(\overset{\rightharpoonup}{OB} \cdot \overset{\rightharpoonup}{OC}\)之值？
(1)\(-4\)
(2)\(\frac{-3}{2}\)
(3)0
(4)\(\frac{\sqrt{39}}{2}\)
(5)\(\frac{7}{2}\)
魯夫、索隆與那美三人自 A 點處出發，已知魯夫沿著 a 方向，每分鐘走 x 公尺；索隆沿著 b 方向每分鐘走 y 公尺；那美沿著 c 方向前進。魯夫讓索隆、那美兩人先走 1 分鐘後再出發。當魯夫走 1 分鐘後到達 B 點時，索隆走到 C 點，且兩人走的路徑長總和為 20 公尺，而那美走到 BC 上一點 P，且\(3\overset{\rightharpoonup}{AP}=\frac{3}{5}\overset{\rightharpoonup}{AB}+t\overset{\rightharpoonup}{AC}\)，若\(\overset{\rightharpoonup}{a} \perp \overset{\rightharpoonup}{b}\)。試選出正確的選項。
(1)\(2x+y=20\)
(2)\(BP:CP=2:3\)
(3)\(\overset{\rightharpoonup}{AP}\)在\(\overset{\rightharpoonup}{AB}\)與\(\overset{\rightharpoonup}{AC}\)上的正射影長比 = 3：4
(4)\(B,C\)兩點距離最小值為 102 公尺
(5)\(\triangle ABP\)面積最大值為 30 平方公尺
設多項式\(f(x)=x^5+99x^4+97x^3-98x^2-x\)，若多項式\(g(x)\)滿足\(g(x+99)=f(x)\)，則\(g(x)\)的所有項之係數和 = ______。
[選填題]設數列\(\langle a_n \rangle\)的前\(n\)項和為\(S_n\)，且\(S_n=2a_n-5\)，n 為正整數，則\(S_{100}\)為______位數。
[選填題]
圖(2)中有四個正六邊形，邊長由大至小分別為\(a_1\)、\(a_2\)、\(a_3\)、\(a_4\)，且滿足\(\frac{a_{n+1}}{a_n} = \frac{1}{2}, n=1,2,3\)。
若\(\overset{\rightharpoonup}{TF} = x\overset{\rightharpoonup}{AB }+ y\overset{\rightharpoonup}{BC}\)，則數對\((x,y) = \underline{\quad }\)。
（化為最簡分數）
某航空公司經濟艙有\(A \sim D\)四種票，每種票的累積里程比例不同，如表(1)。
| 票種 | A | B | C | D |
|---|---|---|---|---|
| 累積里程比例 | $0\%$ | $50\%$ | $75\%$ | $100\%$ |
小南分析自己長期購買該公司某特定航線的經驗發現：購買此航線\(A\)種票的機率為\(\frac{1}{3}\)，購買\(B \sim D\)三種票的機率恰與票種的累積里程比例成反比，則依小南的購票經驗，購買一張該公司此特定航線累積里程比例的期望值為\(\underline{\quad }\)。（四捨五入至整數位）
[選填題]設一個正整數的奇數位數的和稱為\(A\)，偶數位數的和稱為\(B\)，絕對值\(|A – B|\)稱為這個正整數的祕密差。例如：20250118 的奇數位數的和\(A = 8 + 1 + 5 + 0 = 14\)，偶數位數的和\(B = 1 + 0 + 2 + 2 = 5\)，所以 20250118 的祕密差是\(|14 – 5| = 9\)。則祕密差為 25 的六位正整數有\(\underline{\quad }\)個。
[選填題][題組:第18題到第20題]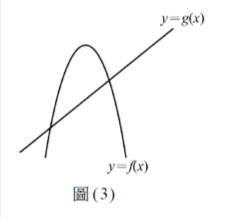
如圖(3)所示，坐標平面上，二次函數\(\Gamma: y = f(x) = a(x + 5)(x – k)\)與一次函數\(L: y = g(x) = m(x + 5)\)相交於\(A \sim B\)兩點，其中\(a \sim k\)，\(m\)為實數。已知\(\Gamma\)的對稱軸為\(x = -2\)，且\(A \sim B\)兩點分別在\(x\)、\(y\)軸上，設\(h(x) = f(x) \cdot g(x)\)，試回答下列問題。
關於\(y = h(x)\)，試選出正確的選項。（多選題，5分）
(1)\(y = h(x)\)的最高次項係數為負
(2)方程式\(h(x) = -1\)有三個相異實根
(3)\(y = h(x)\)經過適當平移可得\(y = amx^3\)的圖形
(4)\(y = h(x)\)圖形對稱中心的\(x\)坐標小於\(-2\)
(5)若\((x + 3)h(x)\)除以\(x + 1\)的餘式為 256，則\(a = -2\)
[題組:第18題到第20題]
若\(y = h(x)\)在\(x = 1\)時的一次近似圖形和直線\(L\)垂直，則\(a^3 = ?\)（非選擇題，5分）
