已知\(a, b\)為正實數,且滿足$\begin{cases}a\sqrt{a}+ b\sqrt{b} = 18\\ \sqrt{a} + \sqrt{b} = 3\end{cases}$,試求\(a + b\)之值。
(1) 5
(2) 6
(3) 7
(4) 8
(5) 9
數學模考
113學測數學A1模考3-02
設集合\(A = \{ x | x \in R, 2|x – \sqrt{3}| = |x+1| \}\),集合\(B = \{ x | x \in R, 2|x – \sqrt{3}| = x+1 \}\),集合\(C = \{ x | x \in R, 2(x – \sqrt{3}) = |x+1| \}\)。試問下列哪一個選項正確?
(1) \(A = B \neq C\)
(2) \(B = C \neq A\)
(3) \(C = A \neq B\)
(4) \(A = B = C\)
(5) \(A \neq B\)且\(B \neq C\)
113學測數學A1模考3-03
關於函數圖形的特性,下列敘述何者錯誤?
(1) $y=\sin x$的函數圖形是點對稱圖形
(2) $y=\cos x$的函數圖形是線對稱圖形
(3) $y=\sin x$的函數圖形經過適當平移後可得到$y=\cos x$的函數圖形
(4) $y = 2^x$和 $y = \log_2x$都是嚴格遞增函數
(5) $y = 2^{-x}$的函數圖形經過適當平移後可得到 $y = -\log_2x$的圖形
113學測數學A1模考3-04
已知\(y = g(x) = 2\cos 2x\)向右平移\(\theta\)後,可和\(y = f(x) = \sin 2x + \sqrt{3} \cos 2x\)重合,其中\(\theta\)為何?
(1) 0
(2) \(\frac{\pi}{12}\)
(3) \(\frac{\pi}{6}\)
(4) \(\frac{\pi}{3}\)
(5) \(\frac{\pi}{2}\)
113學測數學A1模考3-05
等比數列\(\langle a_n \rangle\)的首項為1,且公比為-2。\(\frac{1}{|a_1 – a_2|} + \frac{1}{|a_2 – a_3|} + \frac{1}{|a_3 – a_4|} + \cdots + \frac{1}{|a_{10} – a_{11}|} = \frac{b}{a}\),其中\(a\)、\(b\)為互質的正整數,則\(a-b = ?\)
(1)161
(2)171
(3)181
(4)191
(5)201
113學測數學A1模考3-06
已知圓\(C: x^2 + (y-1)^2 = 10\)和直線\(L: 2x+y = c\)相交於相異兩點\(A\)、\(B\)。令\(O(0,1)\),當\(\triangle OAB\)面積有最大值時,所有可能的值之乘積為何?
(1) -6
(2) -12
(3) -18
(4) -24
(5) -30
113學測數學A1模考3-07
已知\(f(x)\)、\(g(x)\)皆為三次多項式,\(h(x)\)為二次多項式,\(f(x)\)和\(g(x)\)除以\(h(x)\)的餘式為\(r_1(x)\)和\(r_2(x)\),其中\(r_1(x)\)為一次多項式,\(r_2(x)\)為常數多項式。試選出正確的選項。
(1) \(3f(x) + 2g(x)\)必為3次多項式
(2) \(12f(x) + 9g(x)\)除以\(3h(x)\)的餘式為\(4r_1(x) + 3r_2(x)\)
(3) \((3x + 2)g(x)\)除以\(h(x)\)的餘式為\((3x + 2)r_2(x)\)
(4) \(3f(x)\)除以\(x^2 h(x)\)的餘式必為3次多項式
(5) \(f(x)g(x)\)除以\(h(x)\)的餘式必為\(r_1(x)r_2(x)\)
113學測數學A1模考3-08
某音樂公司調查公司內每位歌手某一個月內練習唱歌的小時數及該歌手下個月參加各項歌唱比賽的獲獎次數。令\(x\)表示練習唱歌的小時數,\(y\)表示獲獎次數。若\(y\)對\(x\)的迴歸直線為\(y = \frac{3}{8}x + k\),\(k\)為常數,分別以\(\mu_x, \mu_y, \sigma_x, \sigma_y\)表示\(x\)的算術平均數,\(y\)的算術平均數,\(x\)的標準差,\(y\)的標準差。試選出正確的選項。
(1) 若\(k \gt 0\),則\(\mu_x \lt \mu_y\)
(2) 若\(k \lt 0\),則\(\mu_x \gt \mu_y\)
(3) 若\(\sigma_x = 10\),則\(\sigma_y\)可能為 3
(4) 若\(\sigma_y = 7\),則\(\sigma_x\)可能為 10
(5) 若分別將\(x\)、\(y\)標準化得\(x’\)及\(y’\)則\(y’\)對\(x’\)的迴歸直線為\(y = \frac{3}{8}x\)
113學測數學A1模考3-09
已知滿足方程式\(2^x \cdot 3^y = 12\)的所有實數數對\((x,y)\)在平面上形成一直線\(L\)。試選出正確的選項。
(1) 直線\(L\)通過點\((2,1)\)
(2) 直線\(L\)的斜率為正實數
(3) 直線\(L\)的\(y\)截距為小於3的正數
(4) 直線\(L\)不通過第三象限
(5) 若直線\(L’\)與\(L\)垂直,則直線\(L’\)的斜率為\(\log_2 3\)
113學測數學A1模考3-10
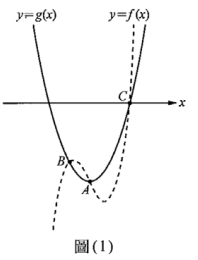 已知三次函數\(y = f(x)\)與二次函數\(y = g(x)\)的圖形相交於\(A(3, -4), B, C\)三點,如圖(1),其中\(A\)為\(y = f(x)\)圖形的對稱中心,也是\(y = g(x)\)圖形的頂點,且點\(C\)在\(x\)軸上,而兩多項式函數的領導係數皆為1。試選出正確的選項。
已知三次函數\(y = f(x)\)與二次函數\(y = g(x)\)的圖形相交於\(A(3, -4), B, C\)三點,如圖(1),其中\(A\)為\(y = f(x)\)圖形的對稱中心,也是\(y = g(x)\)圖形的頂點,且點\(C\)在\(x\)軸上,而兩多項式函數的領導係數皆為1。試選出正確的選項。
(1) \(f(x) = (x-3)^3 – 4\)
(2) \(y = f(x)\)在\(x=3\)附近的一次近似直線斜率為\(-4\)
(3) 若\(f(x)\)除以\(g(x)\)的餘式為\(r(x)\),則\(r(3) = -4\)
(4) \(y = f(x) – g(x)\)的圖形通過\(A, B, C\)三點
(5) 不等式\(f(x) \cdot g(x) \ge 0\)的解為\(x \ge 1\)
