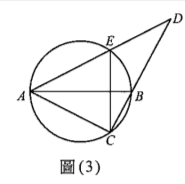
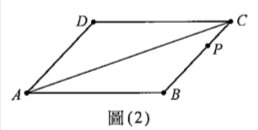
 平行四邊形\(ABCD\),已知\(P\)為\(BC\)上一點,且\(\overrightarrow{AP} = a \overrightarrow{AB} + b \overrightarrow{AD}\),其中\(P \neq B\)且\(P \neq C\),\(\overrightarrow{AQ} = b \overrightarrow{AB} + a \overrightarrow{AD}\),\(\overrightarrow{AR} = (a-0.1)\overrightarrow{AB} + b \overrightarrow{AD}\),\(\overrightarrow{AS} = \frac{1}{2}(\overrightarrow{AP} + \overrightarrow{AC})\)。試選出正確的選項。
平行四邊形\(ABCD\),已知\(P\)為\(BC\)上一點,且\(\overrightarrow{AP} = a \overrightarrow{AB} + b \overrightarrow{AD}\),其中\(P \neq B\)且\(P \neq C\),\(\overrightarrow{AQ} = b \overrightarrow{AB} + a \overrightarrow{AD}\),\(\overrightarrow{AR} = (a-0.1)\overrightarrow{AB} + b \overrightarrow{AD}\),\(\overrightarrow{AS} = \frac{1}{2}(\overrightarrow{AP} + \overrightarrow{AC})\)。試選出正確的選項。
(1) \(Q\)必落在\(CD\)上
(2) \(S\)必落在\(AC\)上
(3) \(R\)必落在\(\triangle ABC\)內部
(4) \(1 \lt a + b \lt 2\)
(5) \(\triangle ACP\)面積與\(\triangle ACQ\)面積相等
數學模考
113學測數學A1模考3-12
某班共有36位學生,某天他們決定用猜拳最輸者擔任當日的值日生,每次猜贏者離開,沒猜贏者繼續猜。但是他們為了要幾個人一組猜拳爭論不休。已知每個人每次出剪刀、石頭、布三種拳的機會均等,假設\(P_n\)為\(n\)個人一組猜拳一次平手的機率,其中\(n \ge 2, n \in N\)。試選出正確的選項。
(1) 甲生說:\(P_3 = \frac{9}{27}\)
(2) 乙生說:\(P_4 = \frac{39}{81}\)
(3) 丙生說:越多人猜拳越容易平手,換句話說,若\(a, b \in N, a \gt b \ge 2\),則\(P_a \gt P_b\)
(4) 丁生說:如果每2人一組猜拳,猜拳一次後,沒猜贏的人數期望值為24人
(5) 戊生說:如果每3人一組猜拳,猜拳一次後,沒猜贏的人數期望值為24人
113學測數學A1模考3-13
平面上有一定點\(A(2, 1)\)及一直線\(L: y = mx\),令\(A\)在\(L\)的投影點為\(A’\),則線段\(AA’\)長最大時的\(m\)值=______。
[選填題]113學測數學A1模考3-14
113學測數學A1模考3-15
四邊形\(ABCD\)中,\(\angle B = 150^\circ, \angle C = 150^\circ, AB = 6, BC = 4, CD = 8\),則四邊形\(ABCD\)的面積______。
[選填題]113學測數學A1模考3-16
設\(a, b\)均為大於1的實數,且\(c\)為不等於1的正實數,若\(2(\log_a c + \log_b c) = 9\log_{ab} c\),則\(\log_a b\)的最小值 = ______。(化為最簡分數)
[選填題]113學測數學A1模考3-17
已知\(a \gt 1\),且在坐標平面的第一象限有\(A, B\)兩點分別在\(y = a^x\)及\(y = \log_a x\)上,使得正三角形\(OAB\)的邊長為\(2\sqrt{6} + 2\sqrt{2}\),其中\(O\)為原點,則\(a = \)______。
[選填題]113學測數學A1模考3-18
113學測數學A1模考3-19
[題組:第18題到第20題]
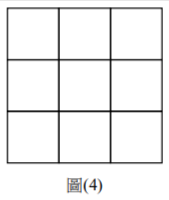
從這9格選取其中5格,每格被選取的機會相等,則選出的這5格恰可以形成1條連線的機率為何?(非選擇題,6分)
113學測數學A1模考3-20
[題組:第18題到第20題]
從這9格選取其中5格,每格被選取的機會相等,則選出的這5格形成的連線數之期望值為何?(非選擇題,6分)