設 \(F_1, F_2\) 為橢圓 \(\Gamma\) 的兩個焦點。\(S\) 為以 \(F_1\) 為中心的正方形(\(S\) 的各邊可不與 \(\Gamma\) 的對稱軸平行)。試問 \(S\) 可能有幾個頂點落在 \(\Gamma\) 上?
(1) 1
(2) 2
(3) 3
(4) 4
(5) 0
104以前學測數學
102學測數學考科-12
設實數組成的數列 \(\lt a_n\gt\) 是公比為 \(-0.8\) 的等比數列,實數組成的數列 \(\lt b_n\gt\) 是首項為 10 的等差數列。已知 \(a_9 > b_9\) 且 \(a_{10} > b_{10}\)。請選出正確的選項。
(1) \(a_9 \times a_{10} < 0\)
(2) \(b_{10} > 0\)
(3) \(b_9 > b_{10}\)
(4) \(a_9 > a_{10}\)
(5) \(a_8 > b_8\)
(1) ○:
∵ \( a_9 \times a_{10} = a_1^2 \times (-0.8)^{17} < 0 \),
∴ 成立。
(2) X:
由 \( a_9 = (-0.8)^8 \cdot a_1 + 8d > 0 \)、
\( a_{10} = (-0.8)^9 \cdot a_1 + 9d < 0 \),
相減得 \( 9d < -0.8^9 a_1 - 8d \),
整理得 \( d < -\dfrac{90}{77} \)。
∴ \( b_{10} = 10 + 9d < 10 - \dfrac{810}{77} = -\dfrac{40}{77} < 0 \)。
(3) ○:
∵ \( d < -\dfrac{90}{77} < 0 \),
∴ \( b_{10} - b_9 = d < 0 \Rightarrow b_{10} < b_9 \)。
(4) ×:不一定。
若 \( a_1 > 0 \),則 \( a_9 > 0 > a_{10} \);
若 \( a_1 < 0 \),則 \( a_9 < 0 < a_{10} \)。
故大小關係不固定。
(5) ×:不一定。
同上,因 \( a_1 \) 正負未定,無法比較 \( a_9 \) 與 \( a_{10} \)。
102學測數學考科-13
設 \(k\) 為一整數。已知 \(\frac{k}{3} < \sqrt{31} < \frac{k + 1}{3}\),則 \(k = \)__________。
[選填]102學測數學考科-14
設 \(a, b\) 為實數且 \((a + bi)(2 + 6i) = -80\),其中 \(i^2 = -1\)。則 \((a, b) =\) (__________,__________)。
[選填]∵ \( (a + bi)(2 + 6i) = -80 \)
⇒ \( (2a - 6b) + (2b + 6a)i = -80 \)
比較實部與虛部得:
\[
\begin{cases}
2a - 6b = -80 \\
2b + 6a = 0
\end{cases}
\Rightarrow
\begin{cases}
a - 3b = -40 \quad \text{⋯①} \\
b = -3a \quad \text{⋯②}
\end{cases}
\]
將②代入①:
\( a + 9a = -40 \Rightarrow 10a = -40 \Rightarrow a = -4 \),
代回②得 \( b = 12 \)。
故解為 \( a = -4 \),\( b = 12 \)。
102學測數學考科-15
坐標平面中 \(A(a, 3)\)、\(B(16, b)\)、\(C(19, 12)\) 三點共線。已知 \(C\) 不在 \(A, B\) 之間,且 \(AC : BC = 3 : 1\),則 \(a + b =\)__________。
[選填]102學測數學考科-16
阿德賣 100 公斤的香蕉,第一天每公斤賣 40 元;沒賣完的部份,第二天降價為每公斤 36 元;第三天再降為每公斤 32 元,到第三天全部賣完,三天所得共為 3720 元。假設阿德在第三天所賣香蕉的公斤數為 \(t\),可算得第二天賣出香蕉的公斤數為 \(at + b\),其中 \(a = \)__________,\(b =\)__________。
[選填]設第一天賣 \( x \) 公斤,第二天賣 \( y \) 公斤,第三天賣 \( t \) 公斤。
由題意得:
\[
\begin{cases}
x + y + t = 100 \quad \text{⋯①} \\
40x + 36y + 32t = 3720 \quad \text{⋯②}
\end{cases}
\]
將②式除以 4 得:
\( 10x + 9y + 8t = 930 \) ⋯②'
①×10 - ②' 得:
\( y + 2t = 70 \Rightarrow y = -2t + 70 \)
故解為:
\( a = -2 \),\( b = 70 \)
102學測數學考科-17
坐標平面上,一圓$C$與直線 \(L_1:x – y = 1\) 以及直線 \(L_2:x – y = 5\) 所截的弦長皆為 $14$。則此圓的面積為 \(\boxed{~~~~~~~~~~}\pi\)。
[選填]102學測數學考科-18
令 \(A\)、\(B\) 為坐標平面上兩向量。已知 \(A\) 的長度為 1,\(B\) 的長度為 2 且 \(A\) 與 \(B\) 之間的夾角為 60°。令 \(u = A + B\),\(v = xA + yB\),其中 \(x, y\) 為實數且符合 \(6 \leq x + y \leq 8\) 以及 \(-2 \leq x – y \leq 0\),則內積 \(u \cdot v\) 的最大值為____________。
[選填]解:
\[
\vec{u} \cdot \vec{v} = (\vec{A} + \vec{B}) \cdot (x\vec{A} + y\vec{B}) = x|\vec{A}|^2 + (x+y)\vec{A}\cdot\vec{B} + y|\vec{B}|^2
\]
由題設 \( |\vec{A}| = 1 \),\( |\vec{B}| = 2 \),\( \angle(\vec{A},\vec{B}) = 60^\circ \),得:
\[
= x + (x+y) \cdot 1 \cdot 2 \cdot \cos 60^\circ + y \cdot 4 = x + (x+y) + 4y = 2x + 5y
\]
利用線型規劃概念,作圖求可行解點:
\[
\begin{array}{c|cccc}
(x, y) & (3,3) & (4,4) & (2,4) & (3,5) \\
\hline
2x+5y & 21 & 28 & 24 & 31 \\
\end{array}
\]
∴ 最大值為 \( 31 \)。
102學測數學考科-19
設銳角三角形 \(ABC\) 的外接圓半徑為 8。已知外接圓圓心到 \(AB\) 的距離為 2,而到 \(BC\) 的距離為 7,則 \(AC =\)__________。
[選填]設 \(\angle OBM = \theta_1\),\(\angle OBN = \theta_2\)
\[
\Rightarrow BM = \sqrt{BO^2 - OM^2} = \sqrt{8^2 - 2^2} = \sqrt{60} = 2\sqrt{15}
\]
\[
BN = \sqrt{BO^2 - ON^2} = \sqrt{8^2 - 7^2} = \sqrt{15}
\]
\[
\therefore \cos\theta_1 = \frac{BM}{BO} = \frac{2\sqrt{15}}{8} = \frac{\sqrt{15}}{4},\quad \sin\theta_1 = \frac{OM}{BO} = \frac{2}{8} = \frac{1}{4}
\]
\[
\cos\theta_2 = \frac{BN}{BO} = \frac{\sqrt{15}}{8},\quad \sin\theta_2 = \frac{ON}{BO} = \frac{7}{8}
\]
\[
\Rightarrow \sin(\angle ABC) = \sin(\theta_1 + \theta_2) = \sin\theta_1 \cos\theta_2 + \cos\theta_1 \sin\theta_2
\]
\[
= \frac{1}{4} \times \frac{\sqrt{15}}{8} + \frac{\sqrt{15}}{4} \times \frac{7}{8} = \frac{\sqrt{15}}{32} + \frac{7\sqrt{15}}{32} = \frac{8\sqrt{15}}{32} = \frac{\sqrt{15}}{4}
\]
\[
\therefore \text{由正弦定理得 } \frac{AC}{\sin(\angle ABC)} = 2R \Rightarrow AC = 2R \cdot \sin(\angle ABC) = 2 \times 8 \times \frac{\sqrt{15}}{4} = 4\sqrt{15}
\]
102學測數學考科-20
如下圖,在坐標空間中,\(A, B, C, D, E, F, G, H\) 為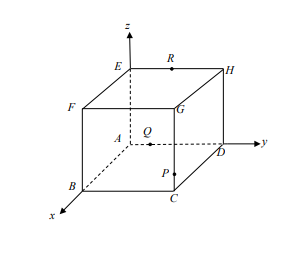 正立方體的八個頂點,已知其中四個點的坐標 \(A(0, 0, 0)\)、\(B(6, 0, 0)\)、\(D(0, 6, 0)\) 及 \(E(0, 0, 6)\),\(P\) 在線段 \(CG\) 上且 \(CP : PG = 1 : 5\),\(R\) 在線段 \(EH\) 上且 \(ER : RH = 1 : 1\),\(Q\) 在線段 \(AD\) 上。若空間中通過 \(P, Q, R\) 這三點的平面,與直線 \(AG\) 不相交,則 \(Q\) 點的 \(y\) 坐標為___________。
正立方體的八個頂點,已知其中四個點的坐標 \(A(0, 0, 0)\)、\(B(6, 0, 0)\)、\(D(0, 6, 0)\) 及 \(E(0, 0, 6)\),\(P\) 在線段 \(CG\) 上且 \(CP : PG = 1 : 5\),\(R\) 在線段 \(EH\) 上且 \(ER : RH = 1 : 1\),\(Q\) 在線段 \(AD\) 上。若空間中通過 \(P, Q, R\) 這三點的平面,與直線 \(AG\) 不相交,則 \(Q\) 點的 \(y\) 坐標為___________。
[選填]
由題意畫得知 \( A(0, 0, 0) \)、\( G(6, 6, 6) \)、\( P(6, 6, 1) \)、\( R(0, 3, 6) \)
設 \( Q(0, k, 0) \)
\[
\overrightarrow{PQ} = Q - P = (-6,\; k-6,\; -1)
\]
\[
\overrightarrow{PR} = R - P = (-6,\; -3,\; 5)
\]
平面 \( PQR \) 的法向量
\[
\overrightarrow{n} = \overrightarrow{PQ} \times \overrightarrow{PR}
\]
\[
= \begin{vmatrix}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
-6 & k-6 & -1 \\
-6 & -3 & 5
\end{vmatrix}
\]
\[
= \mathbf{i} \begin{vmatrix} k-6 & -1 \\ -3 & 5 \end{vmatrix}
-\mathbf{j} \begin{vmatrix} -6 & -1 \\ -6 & 5 \end{vmatrix}
+\mathbf{k} \begin{vmatrix} -6 & k-6 \\ -6 & -3 \end{vmatrix}
\]
\[
= \mathbf{i}\big(5(k-6) - 3\big)
-\mathbf{j}\big((-6)\cdot5 - (-1)(-6)\big)
+\mathbf{k}\big((-6)(-3) - (k-6)(-6)\big)
\]
\[
= (5k - 30 - 3,\; -(-30 - 6),\; 18 + 6k - 36)
\]
\[
= (5k - 33,\; 36,\; 6k - 18)
\]
直線 \( AG \) 的方向向量 \(\overrightarrow{v}\) 平行於 \(\overrightarrow{AG} = (6, 6, 6)\),可取 \(\overrightarrow{v} = (1, 1, 1)\)
若平面 \( PQR \) 與直線 \( AG \) 不相交,則
\[
\overrightarrow{n} \perp \overrightarrow{v} \quad\Rightarrow\quad \overrightarrow{n} \cdot \overrightarrow{v} = 0
\]
\[
(5k - 33) \cdot 1 + 36 \cdot 1 + (6k - 18) \cdot 1 = 0
\]
\[
5k - 33 + 36 + 6k - 18 = 0
\]
\[
11k - 15 = 0
\]
\[
\therefore k = \frac{15}{11}
\]
