下列關於指數與對數的敘述,試選出正確的選項。
(1) \( (\log_{\pi}2)^{\pi} = 2 \)
(2) \( \log_{2} (\pi) + \log_{3} (\pi) = \log_{6} (\pi) \)
(3) \( \pi^{\pi+2} \times \pi^{-2} \gt 27 \)
(4) 函數 \( y = \pi^x \) 的圖形恆在 y 軸右方
(5) 函數 \( y = \log_{\pi} (x) \) 的圖形與函數 \( y = \pi^x \) 的圖形有兩個交點
學測數學
113學測數學A1模考4-02
已知等比數列 \( a_1, a_2, \cdots, a_n \) 共有 n 項,每一項皆為正整數,且 \( a_1 = 1 、 a_n = 2^{20} \)。
試問 n 的值可能為下列哪一個選項?
(1) 20
(2) 15
(3) 12
(4) 10
(5) 5
113學測數學A1模考4-03
在坐標空間中,已知 \( A(1, 2, -3) \) 與 \( B(3, -6, 5) \) 兩點到平面 E 的距離相等,且平面 E 與平面 F:\( 2x + 2y – z = 5 \) 沒有交點,則點 \((4, 0, 2)\) 到平面 E 的距離為何?
(1) 2
(2) \(\frac{7}{3} \)
(3) \( \frac{8}{3} \)
(4) 3
(5) \( \frac{10}{3} \)
113學測數學A1模考4-04
設實數 \( x \gt 0 \),則函數 \( f(x) = -\left( x + \frac{4}{x} \right)^2 – 2\left( x + \frac{4}{x} \right) + 16 \) 的最大值為何?
(1) -8
(2) -19
(3) 8
(4) 13
(5) 17
113學測數學A1模考4-05
甲、乙兩人依下列規則進行遊戲:每次先由甲從1到6中任意選取一數,再由乙投擲一個公正骰子並觀察點數。當甲選取的數字等於乙投擲骰子出現的點數時,稱為「成功」。並繼續這個過程,直到「成功」次數為2時遊戲結束。已知在乙投擲第三次骰子後,遊戲尚未結束,試問乙投擲第四次骰子後,遊戲就結束的機率為何?
(1) \(\frac{1}{4}\) (2) \(\frac{1}{8}\) (3) \(\frac{1}{12}\) (4) \(\frac{1}{16}\) (5) \(\frac{1}{20}\)
113學測數學A1模考4-06
已知三次實係數多項式\(f(x)\)的最高次項係數為2,且函數\(f(x)\)在\(x=1\)附近的近似直線為\(y=-2(x-1)+11\),而\(f(x)\)在\(x=2\)附近的近似直線為\(y=-18(x-2)\)。試問滿足\(f(x-1)\leq0\)的所有正整數之和為下列哪一個選項?
(1) 27 (2) 26 (3) 25 (4) 18 (5) 12
113學測數學A1模考4-07
小廖在夜市玩飛鏢射氣球,攤位上有一個挖有圓形洞口的保麗龍板,並在洞口處塞進一顆氣球,只要將飛鏢射入圓形洞口內部(包含圓周),則必可擊破塞在洞口中的氣球。今建立坐標空間,並設保麗龍板位於yz平面,且圓形洞口的圓心坐標為\(P(0,1,-2)\),半徑為\(\sqrt{5}\),而飛鏢從點\((10,2,1)\)發出,並依向量\(\overrightarrow{v}\)的方向直線射向保麗龍板,試問向量\(\overrightarrow{v}\)等於下列哪些選項時,可順利擊破氣球?
(1) \((-2,-1,0)\)
(2) \((-2,0,0)\)
(3) \((-3,-1,-1)\)
(4) \((-6,-1,-2)\)
(5) \((-5,-1,-1)\)
113學測數學A1模考4-08
給定一實係數三次多項式函數 \( f(x)=ax^3+bx^2+cx+d \),已知 \( f(x)<0 \) 的解為 \(-5\lt x\lt 1\) 或 \( x\gt 1 \),則關於 \( f(x) \) 的敘述,試選出正確的選項。
(1) \( a>0 \)
(2) \( f(x) \) 除以 \( x \) 的餘式為 \(-5 \)
(3) \( y=f(x) \) 圖形對稱中心的 \( x \) 坐標為 \(-1 \)
(4) \( f(40)\lt f(50) \)
(5) 若 \( f(x) \) 在 \( x=-5 \) 附近的近似直線為 \( y=mx+n \),則 \( m<0 \)
113學測數學A1模考4-09
已知函數 \( f(x)=\sin\left(x+\frac{\pi}{6}\right)-\cos\left(x-\frac{\pi}{6}\right) \),試選出正確的選項。
(1) 若 \( 0\leq x<2\pi \),則 \( f(x) \) 的最大值為 \( \frac{\sqrt{6}-\sqrt{2}}{2} \)
(2) 若 \( 0\leq x<2\pi \) 且 \( f(x) \) 在 \( x=a \) 時取得最小值,則 \( a=\frac{7\pi}{4} \)
(3) 函數 \( y=f(x) \) 圖形的週期為 \( \pi \)
(4) 若 \( 0\leq \alpha <\beta <2\pi \) 且 \( f(\alpha)=f(\beta)=\frac{1}{2} \),則 \( \alpha +\beta=\pi \)
(5)若 \( 0 \leq x < 8\pi \) ,則所有滿足方程式 \( f(x) = 0 \) 的相異實數解之和為 \( 30\pi \)
113學測數學A1模考4-10
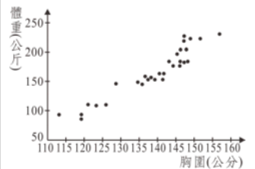 下左圖是某種麋鹿的胸圍 \( x \)(公分)與體重 \( y \)(公斤)的二維數據之散布圖,經過計算可知這 30 隻麋鹿的胸圍 \( x \) 與體重 \( y \) 的算術平均數與標準差如下表。
下左圖是某種麋鹿的胸圍 \( x \)(公分)與體重 \( y \)(公斤)的二維數據之散布圖,經過計算可知這 30 隻麋鹿的胸圍 \( x \) 與體重 \( y \) 的算術平均數與標準差如下表。
| 算術平均數 | 標準差 | |
| 胸圍 \( x \) (公分) | 139.27 | 11.26 |
| 體重 \( y \) (公斤) | 171.27 | 43.83 |
根據上述數據,試選出正確的選項。
(1)從這 30 隻麋鹿中任選一隻,則牠的體重小於 150 公斤的機率大於 18%
(2)從這 30 隻麋鹿中任選一隻,已知牠的胸圍大於 140 公分,則牠的體重大於 200 公斤的條件機率大於 55%
(3)這 30 隻麋鹿體重的中位數大於 180 公斤
(4)y 對 x 的迴歸直線斜率小於 4
(5)利用迴歸直線進行預估,一隻胸圍 160 公分的麋鹿,其體重大
