〈學測數學〉彙整頁面 - 第 46 頁，總計 46 頁

111學測數學B試題-11

考慮坐標平面上的點$O(0,0)$ 、$A$、 $B$、 $C$、 $D$、 $E$、 $F$、 $G$,如下圖所示：
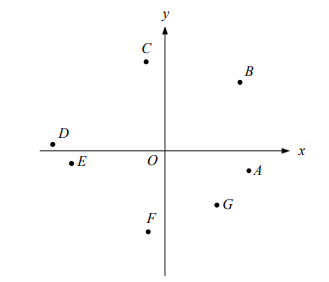其中$B$點、$C$與$D$點、$E$與$F$點、$G$與$A$點依序在一、二、三、四象限內。若$\vec{v}$為坐標平面上的向量,且滿足$\vec{v}\cdot\overrightarrow{OA} \gt 0$及$\vec{v}\cdot\overrightarrow{OB} \gt 0$,則$\vec{v}$與下列哪些向量的內積一定小於$0$ ？
(1) $\overrightarrow{OC}$；
(2) $\overrightarrow{OD}$；
(3) $\overrightarrow{OE}$；
(4) $\overrightarrow{OF}$；
(5) $\overrightarrow{OG}$

[多選]

答案

$\begin{align*}
&若向量與\vec{v}的內積<0，則兩向量夾角為鈍角。\\ &其中\overrightarrow{OD}、\overrightarrow{OE}與\vec{v}的內積均小於0，故選(2)(3)。 \end{align*}$

https://www.ceec.edu.tw/files/file_pool/1/0m053363176747148935/04-111%e5%ad%b8%e6%b8%ac%e6%95%b8%e5%ad%b8b%e9%81%b8%e6%93%87%28%e5%a1%ab%29%e9%a1%8c%e7%ad%94%e6%a1%88.pdf

加最愛

111學測數學B試題-12

設$a$, $b$, $c$都是非零的實數,且二次方程式$ax^{2}+bx + c = 0$的兩根都落在$1$和$3$之間。試選出兩根必定都落在$4$和$5$之間的方程式。
(1) $a(x – 2)^{2}+b(x – 2)+c = 0$；
(2) $a(x + 2)^{2}+b( x + 2)+c = 0$；
(3) $a(2x – 7)^{2}+b(2x – 7)+c = 0$；
(4) $a(2x + 7)^{2}+b(2x + 7)+c = 0$；
(5) $a(3x – 11)^{2}+b(3x – 11)+c = 0$

[多選]

答案

$\begin{align*}
&已知方程ax^2+bx+c=0的根t滿足1\lt t\lt3，需找變換後根在(1,3)內的選項：\\
&(1) ×：1\lt x-2\lt 3 \implies 3\lt x\lt 5，不符合；\\
&(2) ×：1\lt x+2\lt 3 \implies -1\lt x\lt 1，不符合；\\
&(3) ○：1\lt 2x-7\lt 3 \implies 8\lt 2x\lt 10 \implies 4\lt x\lt 5，符合；\\
&(4) ×：1\lt \frac{x+7}{2}\lt 3 \implies -5\lt x\lt -1，不符合；\\
&(5) ○：1\lt 3x-11\lt 3 \implies 12\lt 3x\lt 14 \implies 4\lt x\lt \frac{14}{3}\lt 5，符合；\\
\\
&故選(3)(5)。
\end{align*}$

https://www.ceec.edu.tw/files/file_pool/1/0m053363176747148935/04-111%e5%ad%b8%e6%b8%ac%e6%95%b8%e5%ad%b8b%e9%81%b8%e6%93%87%28%e5%a1%ab%29%e9%a1%8c%e7%ad%94%e6%a1%88.pdf

加最愛

111學測數學B試題-13

若 $ x, y $ 為兩正實數，且滿足 $ x^{\frac{-1}{3}}y^2 = 1 $ 及 $ 2 \log y = 1 $，則 $ \frac{x – y^2}{10} = \boxed{\phantom{00}} \boxed{\phantom{00}} $。

[選填]

答案

1. 由 $ 2 \log y = 1 $ 得
\[
\log y = \frac{1}{2} \quad \Rightarrow \quad y = 10^{1/2} = \sqrt{10}.
\]
因此
2. 由 $ x^{-1/3} y^2 = 1 $ 得
\[
x^{-1/3} \cdot 10 = 1 \quad \Rightarrow \quad x^{-1/3} = \frac{1}{10}.
\]
取倒數再立方：
\[
x^{1/3} = 10 \quad \Rightarrow \quad x = 10^3 = 1000.
\]

3. 計算
\[
\frac{x - y^2}{10} = \frac{1000 - 10}{10} = \frac{990}{10} = 99.
\]

**答案：** $ \boxed{99} $

https://www.ceec.edu.tw/files/file_pool/1/0m053363176747148935/04-111%e5%ad%b8%e6%b8%ac%e6%95%b8%e5%ad%b8b%e9%81%b8%e6%93%87%28%e5%a1%ab%29%e9%a1%8c%e7%ad%94%e6%a1%88.pdf

加最愛

111學測數學B試題-14

坐標平面上有一個半徑為$7$的圓,其圓心為$O$點。已知圓上有$A$, $B$兩點,且$AB = 8$ ,則內積$\overrightarrow{OA}\cdot\overrightarrow{OB}=\underline{○14 – 1}\ \underline{○14 – 2}$ 。

[選填]

答案

在$\triangle AOB$中,$\vert\overrightarrow{OA}\vert=\vert\overrightarrow{OB}\vert = 7$,$\vert\overrightarrow{AB}\vert = 8$。根據余弦定理$\cos\angle AOB=\frac{\vert\overrightarrow{OA}\vert^{2}+\vert\overrightarrow{OB}\vert^{2}-\vert\overrightarrow{AB}\vert^{2}}{2\vert\overrightarrow{OA}\vert\vert\overrightarrow{OB}\vert}=\frac{7^{2}+7^{2}-8^{2}}{2\times7\times7}=\frac{49 + 49 - 64}{98}=\frac{34}{98}=\frac{17}{49}$。則$\overrightarrow{OA}\cdot\overrightarrow{OB}=\vert\overrightarrow{OA}\vert\vert\overrightarrow{OB}\vert\cos\angle AOB = 7\times7\times\frac{17}{49}=17$。即$\underline{○14 - 1}=17$,$\underline{○14 - 2}=0$。

https://www.ceec.edu.tw/files/file_pool/1/0m053363176747148935/04-111%e5%ad%b8%e6%b8%ac%e6%95%b8%e5%ad%b8b%e9%81%b8%e6%93%87%28%e5%a1%ab%29%e9%a1%8c%e7%ad%94%e6%a1%88.pdf

加最愛

111學測數學B試題-15

根據某國對失蹤輕航機的調查得知：失蹤輕航機中有$70\%$後來會被找到,在被找到的輕航機當中,有$60\%$裝設緊急定位傳送器；而沒被找到的失蹤輕航機當中,則有$90\%$未裝設緊急定位傳送器。緊急定位傳送器會在飛機失事墜毀時發送訊號,讓搜救人員可以定位。現有一架輕航機失蹤,若已知該機有裝設緊急定位傳送器,則它會被找到的機率為___________。（化為最簡分數）

[選填]

答案

1. 設事件$A$表示“輕航機被找到”,事件$B$表示“輕航機裝設緊急定位傳送器”。
2. 已知$P(A)=0.7$,$P(B|A)=0.6$,$P(\overline{A}) = 1 - 0.7 = 0.3$,$P(\overline{B}|\overline{A}) = 0.9$,則$P(B|\overline{A}) = 1 - 0.9 = 0.1$。
3. 由全機率公式$P(B)=P(A)P(B|A)+P(\overline{A})P(B|\overline{A}) = 0.7×0.6 + 0.3×0.1 = 0.42 + 0.03 = 0.45$。
4. 再根據貝葉斯公式$P(A|B)=\frac{P(A)P(B|A)}{P(B)}=\frac{0.7×0.6}{0.45}=\frac{42}{45}=\frac{14}{15}$,即$\underline{○15 - 1}=14$。

https://www.ceec.edu.tw/files/file_pool/1/0m053363176747148935/04-111%e5%ad%b8%e6%b8%ac%e6%95%b8%e5%ad%b8b%e9%81%b8%e6%93%87%28%e5%a1%ab%29%e9%a1%8c%e7%ad%94%e6%a1%88.pdf

加最愛

111學測數學B試題-16

袋中有藍、綠、黃三種顏色的球共 10 顆。今從袋中隨機抽取兩顆球（每顆球被抽中的機率相等），若抽出的兩顆球皆為藍色的機率為 $\frac{1}{15}$，皆為綠色的機率為 $\frac{2}{9}$，則從袋中隨機抽出兩球，此兩球為相異顏色的機率為 ______（化為最簡分數）。

[選填]

答案

設藍、綠、黃球數分別為 $a, b, c$，則
\[
a + b + c = 10
\]

1. 兩球皆藍的機率：
\[
\frac{C^a_2}{C^{10}_2} = \frac{a(a-1)/2}{45} = \frac{a(a-1)}{90} = \frac{1}{15}
\]
\[
a(a-1) = 6 \quad \Rightarrow \quad a^2 - a - 6 = 0
\]
\[
(a-3)(a+2) = 0 \quad \Rightarrow \quad a = 3 \quad (\text{取正})
\]

2. 兩球皆綠的機率：
\[
\frac{C^b_2}{45} = \frac{b(b-1)/2}{45} = \frac{b(b-1)}{90} = \frac{2}{9}
\]
\[
b(b-1) = 20 \quad \Rightarrow \quad b^2 - b - 20 = 0
\]
\[
(b-5)(b+4) = 0 \quad \Rightarrow \quad b = 5
\]

3. 因此
\[
c = 10 - a - b = 10 - 3 - 5 = 2
\]

4. 兩球同色的機率：
\[
P_{\text{同}} = \frac{C^3_2 + C^5_2 + C^2_2}{45}
= \frac{3 + 10 + 1}{45} = \frac{14}{45}
\]

5. 兩球異色的機率：
\[
P_{\text{異}} = 1 - \frac{14}{45} = \frac{31}{45}
\]

**答案：** $\boxed{\frac{31}{45}}$

https://www.ceec.edu.tw/files/file_pool/1/0m053363176747148935/04-111%e5%ad%b8%e6%b8%ac%e6%95%b8%e5%ad%b8b%e9%81%b8%e6%93%87%28%e5%a1%ab%29%e9%a1%8c%e7%ad%94%e6%a1%88.pdf

加最愛

111學測數學B試題-17

有三女三男共六位在學校時和老師常有互動的同學,畢業後老師邀聚餐,餐後七人站一橫排照相留念。已知同學中有一女一男兩位曾有過不愉快,照相時不想相鄰,而老師站在正中間且三位男生不完全站在老師的同一側,則可能的排列方式共有$\underline{○17 – 1}\ \underline{○17 – 2}\ \underline{○17 – 3}$種。

[選填]

答案

$\begin{align*}
&總排列數：6!=720種。\\
\\
&不合情形（無交集）：\\
&① 男女各一側：3!×3!×2=72種（3男、3女分側，兩側可交換）；\\
&② AB相鄰：將AB視為整體，共4個相鄰位置，AB排列有2種，其餘4人排列有4!種，\\
&\quad 故n(AB相鄰)=4×2×4!=192種；\\
\\
&符合條件的排列數：720-72-192=456種。
\end{align*}$

https://www.ceec.edu.tw/files/file_pool/1/0m053363176747148935/04-111%e5%ad%b8%e6%b8%ac%e6%95%b8%e5%ad%b8b%e9%81%b8%e6%93%87%28%e5%a1%ab%29%e9%a1%8c%e7%ad%94%e6%a1%88.pdf

加最愛

111學測數學B試題-18

18-20 題為題組
瘦長的塔因為年代久遠，塔身容易傾斜。在下方右圖中，以粗黑線條代表塔身，而塔身的長度稱為塔高，塔身與鉛直虛線的夾角稱為該塔的傾斜度（ $0\le 90$），又塔頂至鉛直虛線的距離稱為該塔的偏移距離。
已知世界上傾斜度最高的摩天大樓坐落於阿布達比,其傾斜度達到$18^{\circ}$,此傾斜度換算成弳（或弧度）為下列哪一個選項？
(1) $\frac{\pi}{36}$；
(2) $\frac{\pi}{18}$；
(3) $\frac{\pi}{20}$；
(4) $\frac{\pi}{10}$；
(5) $\frac{\pi}{8}$

[單選]

答案

1. 因為$180^{\circ}=\pi$弧度,設$18^{\circ}$對應的弧度為$x$。
2. 則由比例關系可得$\frac{180^{\circ}}{\pi}=\frac{18^{\circ}}{x}$。
3. 解得$x=\frac{18\pi}{180}=\frac{\pi}{10}$。答案：(4)

https://www.ceec.edu.tw/files/file_pool/1/0m053363176747148935/04-111%e5%ad%b8%e6%b8%ac%e6%95%b8%e5%ad%b8b%e9%81%b8%e6%93%87%28%e5%a1%ab%29%e9%a1%8c%e7%ad%94%e6%a1%88.pdf

加最愛

111學測數學B試題-19

18-20為題組
中國虎丘塔、護珠塔與義大利的比薩斜塔是三座著名斜塔,它們的塔高分別為$48$、$19$與$57$（公尺）,偏移距離分別為$2.3$、$2.3$與$4$（公尺）,塔的傾斜度分別記為$\theta_{1}^{\circ}$、$\theta_{2}^{\circ}$與$\theta_{3}^{\circ}$。試比較$\theta_{1}$、$\theta_{2}$與$\theta_{3}$三數的大小關係。

[非選擇]

答案

$\begin{align*}
&由「\frac{偏移距離}{塔高}=\sin\theta」，計算各角度對應的\sin\theta：\\
&\sin\theta_1^\circ=\frac{2.3}{48}\approx0.05，\\
&\sin\theta_2^\circ=\frac{2.3}{19}\approx0.12，\\
&\sin\theta_3^\circ=\frac{4}{57}\approx0.07。\\
\\
&因\sin\theta在(0^\circ,90^\circ)遞增，故\sin\theta_2^\circ>\sin\theta_3^\circ>\sin\theta_1^\circ \implies \theta_2>\theta_3>\theta_1。
\end{align*}$

https://www.ceec.edu.tw/files/file_pool/1/0m053363176747148935/04-111%e5%ad%b8%e6%b8%ac%e6%95%b8%e5%ad%b8b%e9%81%b8%e6%93%87%28%e5%a1%ab%29%e9%a1%8c%e7%ad%94%e6%a1%88.pdf

加最愛

111學測數學B試題-20

18-20為題組
假設有塔高相等的兩座鐵塔,它們的傾斜度$\alpha^{\circ}$,$\beta^{\circ}$分別滿足$\sin\alpha^\circ=\frac{1}{3}$與$\sin\beta^\circ=\frac{1}{6}$。已知兩座鐵塔的偏移距離相差$20$公尺,試求它們的塔頂到地面之距離相差多少公尺。

[非選擇]

答案

$\begin{align*}
&設塔高為H公尺，由偏移距離差得：\\
&H\sin\beta^\circ - H\sin\alpha^\circ = \left(\frac{7}{25} - \frac{1}{5}\right)H = \frac{2}{25}H = 20 \implies H=250。\\
\\
&由\sin\alpha^\circ=\frac{1}{5}得\cos\alpha^\circ=\frac{2\sqrt{6}}{5}，由\sin\beta^\circ=\frac{7}{25}得\cos\beta^\circ=\frac{24}{25}。\\
\\
&計算塔頂到地面距離的差：\\
&H\cos\alpha^\circ - H\cos\beta^\circ = 250×\frac{2\sqrt{6}}{5} - 250×\frac{24}{25} = 100\sqrt{6} - 240（公尺）。
\end{align*}$

https://www.ceec.edu.tw/files/file_pool/1/0m053363176747148935/04-111%e5%ad%b8%e6%b8%ac%e6%95%b8%e5%ad%b8b%e9%81%b8%e6%93%87%28%e5%a1%ab%29%e9%a1%8c%e7%ad%94%e6%a1%88.pdf

加最愛

Saved articles