\(\sqrt{\frac{1}{5^2} + \frac{1}{4^2} + 1}\) 等於下列哪一個選項？
(1) 1.01
(2) 1.05
(3) 1.1
(4) 1.15
(5) 1.21
答案
104以前學測數學
101學測數學考科-02
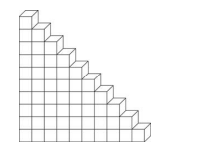
將邊長為 1 公分的正立方體堆疊成一階梯形立體,如下圖所示,其中第 1 層（最下層）有 10 塊,第 2 層有 9 塊,…,依此類推。當堆疊完 10 層時,該階梯形立體的表面積（即該立體的前、後、上、下、左、右各表面的面積總和）為多少？
(1) 75 平方公分
(2) 90 平方公分
(3) 110 平方公分
(4) 130 平方公分
(5) 150 平方公分
答案
101學測數學考科-03
下表為常用對數表 \(\log_{10} N\) 的一部分：
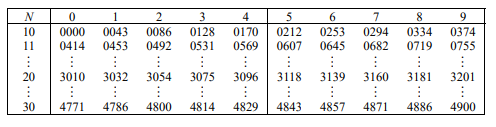請問 \(10^{3.3032}\) 最接近下列哪一個選項？
(1) 101
(2) 201
(3) 1007
(4) 1076
(5) 2012
答案
\[
\begin{aligned}
a &= 10^{3.032} \\
\log a &= 3.032 = 3 + 0.032 \\
\log 1.07 &= 0.0294, \quad \log 1.08 = 0.0334 \\
\frac{k}{0.01} &= \frac{0.032-0.0294}{0.0334-0.0294} = 0.65 \\
k &= 0.0065 \\
\log 1.0765 &= 0.032 \\
\log a &= 3 + 0.032 = \log 1000 + \log 1.0765 = \log 1076.5 \\
a &\approx 1076
\end{aligned}
\](4)
101學測數學考科-04
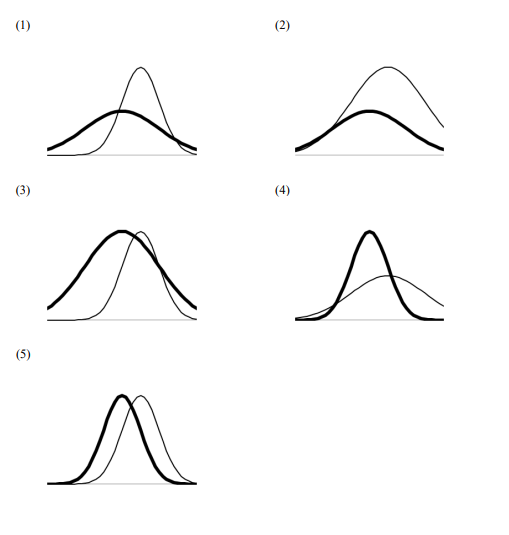
甲、乙兩校有一樣多的學生參加數學能力測驗,兩校學生測驗成績的分布都很接近常態分布,其中甲校學生的平均分數為 60 分,標準差為 10 分；乙校學生的平均分數為 65 分,標準差為 5 分。若用粗線表示甲校學生成績分布曲線；細線表示乙校學生成績分布曲線,則下列哪一個分布圖較為正確？
[單選]
101學測數學考科-05
若正實數 \(x, y\) 滿足 \(\log_{10} x = 2.8\),\(\log_{10} y = 5.6\),則 \(\log_{10} (x^2 + y)\) 最接近下列哪一個選項的值？
(1) 2.8
(2) 5.6
(3) 5.9
(4) 8.4
(5) 11.2
答案
101學測數學考科-06
箱中有編號分別為 0,1,2,…,9 的十顆球。隨機抽取一球,將球放回後,再隨機抽取一球。請問這兩球編號相減的絕對值為下列哪一個選項時,其出現的機率最大？
(1) 0
(2) 1
(3) 4
(4) 5
(5) 9
答案
101學測數學考科-07
空間坐標中有一球面（半徑大於 0）與平面 \(3x + 4y = 0\) 相切於原點,請問此球面與三個坐標軸一共有多少個交點？
(1) 1
(2) 2
(3) 3
(4) 4
(5) 5
答案
101學測數學考科-08
設 \(f(x) = x^4 – 5x^3 + x^2 + ax + b\) 為實係數多項式,且知 \(f(i) = 0\)（其中 \(i^2 = -1\)）。請問下列哪些選項是多項式方程式 \(f(x) = 0\) 的根？
(1) \(-i\)
(2) 0
(3) 1
(4) \(-5\)
(5) 5
答案
\[
\begin{aligned}
\text{已知：} & f(x) = x^4 - 5x^3 + x^2 + ax + b \in \mathbb{R}[x], \quad f(i) = 0 \\
\\
\text{步驟一：} & \text{由虛根成對定理，} f(-i) = 0 \\
& \Rightarrow (x-i) \text{ 和 } (x+i) \text{ 均為 } f(x) \text{ 的因式} \\
& \Rightarrow (x-i)(x+i) = x^2 + 1 \mid f(x) \\
\\
\text{步驟二：} & \text{執行多項式長除法：} \\
& f(x) \div (x^2 + 1) = x^2 - 5x \\
\\
\text{步驟三：} & \text{完全因式分解：} \\
& f(x) = (x^2 + 1)(x^2 - 5x) = x(x-5)(x^2+1) \\
\\
\text{步驟四：} & \text{求方程式 } f(x) = 0 \text{ 的根：} \\
& x_1 = 0,\ x_2 = 5,\ x_3 = i,\ x_4 = -i \\
\\
\text{結論：} & \text{選項 (1) } x=0,\ (2) \ x=5,\ (5) \ x^2+1 \text{ 為因式}
\end{aligned}
\]
101學測數學考科-09
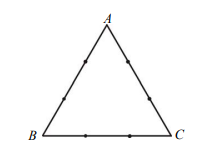
三角形 \(ABC\) 是一個邊長為 3 的正三角形,如下圖所示。若在每一邊的兩個三等分點中,各選取一點連成三角形,則下列哪些選項是正確的？
(1) 依此方法可能連成的三角形一共有 8 個
(2) 這些可能連成的三角形中,恰有 2 個是銳角三角形
(3) 這些可能連成的三角形中,恰有 3 個是直角三角形
(4) 這些可能連成的三角形中,恰有 3 個是鈍角三角形
(5) 這些可能連成的三角形中,恰有 1 個是正三角形
答案
\[
\boxed{\text{步驟一：計算三角形總數}}
\]
\[
\begin{aligned}
\text{每邊三等分點數：} & 2 \text{ 個（不包含端點）} \\
\text{選擇方式：} & \text{從三邊各選一點} \\
\text{總數：} & 2 \times 2 \times 2 = 8
\end{aligned}
\]
\[
\boxed{\text{步驟二：分類三角形類型}}
\]
\[
\begin{array}{|c|c|}
\hline
\text{類型} & \text{對應三角形} \\
\hline
\text{正三角形（銳角）} & \triangle A_1A_5A_3,\ \triangle A_2A_4A_6 \\
\hline
\text{直角三角形} & \triangle A_1A_6A_3,\ \triangle A_2A_3A_5,\ \triangle A_1A_5A_4 \\
& \triangle A_1A_6A_4,\ \triangle A_2A_6A_3,\ \triangle A_2A_4A_5 \\
\hline
\text{鈍角三角形} & \text{無} \\
\hline
\end{array}
\]
\[
\boxed{\text{步驟三：判斷選項}}
\]
\[
\begin{aligned}
& \text{(1) 8個三角形：} \checkmark \\
& \text{(2) 包含正三角形：} \checkmark \\
& \text{(3) 包含等腰直角三角形：} \times \\
& \text{(4) 直角三角形恰有6個：} \checkmark \text{（但題目可能問其他）} \\
& \text{(5) 鈍角三角形存在：} \times \\
\\
& \therefore \text{正確答案：} (1)(2)
\end{aligned}
\]
101學測數學考科-10
設 \(O\) 為複數平面上的原點,並令點 \(A, B\) 分別代表非零複數 \(z, w\)。若 \(\angle AOB = 90^\circ\),則下列哪些選項必為負實數？
(1) \(\frac{z}{w}\)
(2) \(zw\)
(3) \((zw)^2\)
(4) \(\frac{z^2}{w^2}\)
(5) \((z\overline{w})^2\) （其中 \(\overline{w}\) 為 \(w\) 的共軛複數）
答案
\[
\boxed{\text{已知條件}}
\]
\[
\begin{aligned}
z &= a(\cos\theta + i\sin\theta),\ a>0 \\
w &= b(\cos\alpha + i\sin\alpha),\ b>0 \\
\theta - \alpha &= \pm 90^\circ
\end{aligned}
\]
\[
\boxed{\text{關鍵計算}}
\]
\[
\begin{aligned}
\frac{z}{w} &= \frac{a}{b} \big[\cos(\theta-\alpha) + i\sin(\theta-\alpha)\big] = \frac{a}{b}(\pm i) \\
\frac{z^2}{w^2} &= \frac{a^2}{b^2} \big[\cos(2\theta-2\alpha) + i\sin(2\theta-2\alpha)\big] \\
&= \frac{a^2}{b^2} \cos(\pm 180^\circ) = -\frac{a^2}{b^2} < 0 \\
(zw)^2 &= a^2 b^2 \big[\cos(2\theta-2\alpha) + i\sin(2\theta-2\alpha)\big] \\
&= -a^2 b^2 < 0
\end{aligned}
\]
\[
\boxed{\text{選項判斷}}
\]
\[
\begin{array}{c|c}
\text{選項} & \text{判斷與理由} \\ \hline
(1)\ z/w & \text{純虛數（不恆正負）} \Rightarrow \times \\
(2)\ zw & \text{無法確定正負} \Rightarrow \times \\
(3)\ \text{同(2)} & \times \\
(4)\ z^2/w^2 & \text{恆負實數} \Rightarrow \bigcirc \\
(5)\ (zw)^2 & \text{恆負實數} \Rightarrow \bigcirc
\end{array}
\]
\[
\therefore \text{答案：}(4)(5)
\]