有一個三角形公園，其三頂點為 $O$、$A$、$B$，在頂點 $O$ 處有一座 150 公尺高的觀景台，某人站在觀景台上觀測地面上另兩個頂點 $A$、$B$ 與 $AB$ 的中點 $C$，測得其俯角分別為 $30^\circ$、$60^\circ$、$45^\circ$。則此三角形公園的面積為 【 】 平方公尺。（化成最簡根式）
[選填題]指考分科數學-甲
109指考數學甲試題_12
坐標平面上，由 $A$、$B$、$C$、$D$ 四點所決定的「貝茲曲線」（Bézier curve）指的是次數不超過 3 的多項式函數，其圖形通過 $A$、$D$ 兩點，且在點 $A$ 的切線通過點 $B$，在點 $D$ 的切線通過點 $C$。令 $y = f(x)$ 是由 $A(0,0)$、$B(1,4)$、$C(3,2)$、$D(4,0)$ 四點所決定的「貝茲曲線」，試回答下列問題。
設 $y = f(x)$ 的圖形在點 $D$ 的切線方程式為 $y = ax + b$，其中 $a$、$b$ 為實數。求 $a$、$b$ 之值。（2分）
109指考數學甲試題_13
109指考數學甲試題_14
[題組:一(1)到一(4)] 試求 $f(x)$。（4分）
[非選擇題]109指考數學甲試題_15
109指考數學甲試題_16
一個邊長為 1 的正立方體 $ABCD\text{-}EFGH$，點 $P$ 為
稜邊 $CG$ 的中點，點 $Q$、$R$ 分別在稜邊 $BF$、$DH$ 上，且 $A$、$Q$、$P$、$R$ 為一平行四邊形的四個頂點。今設定坐標系，使得 $D(0,0,0)$、$A(1,0,0)$、$C(0,1,0)$、$H(0,0,1)$，且 $BQ = t$，試回答下列問題。
試求點 $P$ 的坐標。（2分）
109指考數學甲試題_17
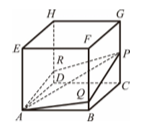
[題組:二(1)到二(4)] 試求向量 $\vec{AR}$（以 $t$ 的式子來表示）。（2分）
[非選擇題]109指考數學甲試題_18
[題組:二(1)到二(4)] 試證明四角錐 $G\text{-}AQPR$ 的體積是一個定值（與 $t$ 無關），並求此定值。（4分）
[非選擇題]109指考數學甲試題_19
[題組:二(1)到二(4)] 當 $t = \dfrac{1}{4}$ 時，求點 $G$ 到平行四邊形 $AQPR$ 所在平面的距離。（4分）
[非選擇題]114分科測驗數學甲試卷-01
坐標平面上,函數 \(y=\sin x\) 的圖形關於 \(x=\frac{\pi}{2}\) 對稱,如圖所示。試求出在 \(0<\theta \leq\pi\) 的範圍中滿足 \(\sin \theta=\sin \left(\theta+\frac{\pi}{5}\right)\) 的 \(\theta\) 值？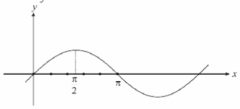
\((1) \frac{\pi}{5}\)
\((2) \frac{2\pi}{5}\)
\((3) \frac{3\pi}{5}\)
\((4) \frac{4\pi}{5}\)
\((5) \pi\)
答案
1. 由 \(\sin \theta = \sin \left(\theta+\frac{\pi}{5}\right)\)，依性質：\(\sin A = \sin B\) 則 \(A = B + 2k\pi\) 或 \(A = \pi - B + 2k\pi\)（\(k\in\mathbb{Z}\)）；
2. 前者得 \(\frac{\pi}{5}=2k\pi\)，無解；後者得 \(2\theta = \frac{4\pi}{5}+2k\pi\)，即 \(\theta = \frac{2\pi}{5}+k\pi\)；
3. 結合 \(0<\theta \leq\pi\)，僅 \(k=0\) 時 \(\theta=\frac{2\pi}{5}\) 符合。答案：(2) \(\frac{2\pi}{5}\)","是