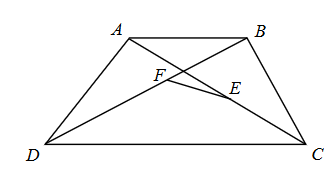
考慮一梯形\(ABCD\),其中\(\overline{AB}\)與\(\overline{DC}\)平行。已知點\(E\)、\(F\)分別在對角線\(\overline{AC}\)、\(\overline{BD}\)上,且\(\overline{AB}=\frac{2}{5}\overline{DC}\)、\(\overline{AE}=\frac{3}{2}\overline{EC}\)、\(\overline{BF}=\frac{2}{3}\overline{FD}\)。若將向量\(\overrightarrow{FE}\)表示成\(\alpha\overrightarrow{AC}+\beta\overrightarrow{AD}\),則實數\(\alpha=\)___________,\(\beta=\)__________(化成最簡分數)
[選填]連線段AF
\(
\begin{align*}
\overrightarrow{FE} &= \overrightarrow{AE} - \overrightarrow{AF} \\
&= \frac{3}{5}\overrightarrow{AC} - \left( \frac{3}{5}\overrightarrow{AB} + \frac{2}{5}\overrightarrow{AD} \right) \\
&= \frac{3}{5}\overrightarrow{AC} - \frac{3}{5} \times \frac{2}{5}\overrightarrow{DC} - \frac{2}{5}\overrightarrow{AD} \\
&= \frac{3}{5}\overrightarrow{AC} - \frac{6}{25} \left( \overrightarrow{AC} - \overrightarrow{AD} \right) - \frac{2}{5}\overrightarrow{AD} \\
&= \frac{3}{5}\overrightarrow{AC} - \frac{6}{25}\overrightarrow{AC} + \frac{6}{25}\overrightarrow{AD} - \frac{2}{5}\overrightarrow{AD} \\
&= \frac{9}{25}\overrightarrow{AC} - \frac{4}{25}\overrightarrow{AD}
\end{align*}
\)
故\(\alpha = \frac{9}{25}\),\(\beta = -\frac{4}{25}\)。