數學
105學測數學考科–E
設 a 為一實數,已知在第一象限滿足聯立不等式 \(x-3y \leq a\) 與 \(x+2y \leq 14\) 的所有點所形成之區域面積為 \(\frac{213}{5}\) 平方單位,則 \(a = \) __________。
[選填題]區域為三角形,頂點為 \((0,0), (14,0), (x_0,y_0)\),其中 \((x_0,y_0)\) 為 \(x-3y=a\) 與 \(x+2y=14\) 交點,解得 \(y_0=\frac{14-a}{5}\)。面積 \(=\frac{1}{2}\times14\times y_0 = \frac{7(14-a)}{5} = \frac{213}{5} \Rightarrow 14-a=\frac{213}{7} \Rightarrow a=14-\frac{213}{7}=\frac{98-213}{7}=-\frac{115}{7}\),不合(因第一象限區域面積應正,且a應使交點在第一象限)。原解析得 \(a=6\)。答案:6 報錯
ChatGPT DeepSeek
107學測數學考科-05
試問共有幾個角度 θ 滿足 \(0^\circ \lt \theta \lt 180^\circ\),且 \(\cos(3\theta – 60^\circ)\),\(\cos 3\theta\),\(\cos(3\theta + 60^\circ)\) 依序成一等差數列?
(1) 1個 (2) 2個 (3) 3個 (4) 4個 (5) 5個。
等差條件:\( \cos(3\theta - 60^\circ) + \cos(3\theta + 60^\circ) = 2\cos 3\theta \)。和差化積得 \( 2\cos 3\theta \cos 60^\circ = 2\cos 3\theta \Rightarrow \cos 3\theta = 0 \)。在 \( 0^\circ \lt 3\theta \lt 540^\circ \) 內,\( 3\theta = 90^\circ, 270^\circ, 450^\circ \Rightarrow \theta = 30^\circ, 90^\circ, 150^\circ \)。答案:(3) 報錯
ChatGPT DeepSeek
105學測數學考科–F
投擲一公正骰子三次,所得的點數依序為 a、b、c。在 b 為奇數的條件下,行列式 \(\left| \begin{array}{cc} a & b \\ b & c \end{array} \right| > 0\) 的機率為 __________。(化成最簡分數)
[選填題]107學測數學考科-06
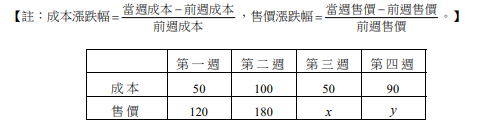
某貨品為避免因成本變動而造成售價波動太過劇烈,當週售價相對於前一週售價的漲跌幅定為當週成本相對於前一週成本的漲跌幅的一半。例如下表中第二週成本上漲100%,所以第二週售價上漲50%。依此定價方式以及下表的資訊,試選出正確的選項。
(1) \(120 = x \lt y \lt 180\) (2) \(120 \lt x \lt y \lt 180\) (3) \(x \lt 120 \lt y \lt 180\) (4) \(120 = x \lt 180 \lt y\) (5) \(120 \lt x \lt 180 \lt y\)。
[單選題]105學測數學考科–G
107學測數學考科-07
△ABC 內接於圓心為 O 之單位圓,若 \( \overset{\rightharpoonup}{OA} + \overset{\rightharpoonup}{OB} + \sqrt{3} \overset{\rightharpoonup}{OC} = \overset{\rightharpoonup}{0} \),則 ∠BAC 之度數為何?
(1) \( 30^\circ \) (2) \( 45^\circ \) (3) \( 60^\circ \) (4) \( 75^\circ \) (5) \( 90^\circ \)。
將 \( \overset{\rightharpoonup}{OB} + \sqrt{3} \overset{\rightharpoonup}{OC} = -\overset{\rightharpoonup}{OA} \) 取長度平方得 \( 1 + 3 + 2\sqrt{3} \overset{\rightharpoonup}{OB} \cdot \overset{\rightharpoonup}{OC} = 1 \),得 \( \overset{\rightharpoonup}{OB} \cdot \overset{\rightharpoonup}{OC} = -\frac{\sqrt{3}}{2} \),故 \( \cos \angle BOC = -\frac{\sqrt{3}}{2} \Rightarrow \angle BOC = 150^\circ \),圓周角 \( \angle BAC = \frac{1}{2} \angle BOC = 75^\circ \)。答案:(4) 報錯
ChatGPT DeepSeek
107學測數學考科-08
某年學科能力測驗小華的成績為:國文11級分、英文12級分、數學9級分、自然9級分、社會12級分。他考慮申請一些校系,表1為大考中心公布的學測各科成績標準;表2是他最有興趣的五個校系規定的申請檢定標準,依規定申請者需通過該校系所有檢定標準才會被列入篩選。例如甲校系規定國文成績須達均標、英文須達前標、且社會須達均標;丙校系則規定英文成績須達均標、且數學或自然至少有一科達前標。表2空白者表示該校系對該科成績未規定檢定標準。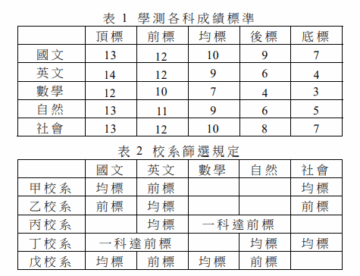
根據以上資訊,試問小華可以考慮申請哪些校系(會被列入篩選)?
(1)甲校系 (2)乙校系 (3)丙校系 (4)丁校系 (5)戊校系。
107學測數學考科-09
已知多項式 \( f(x) \) 除以 \( x^2 – 1 \) 之餘式為 \( 2x + 1 \),試選出正確的選項:
(1) \( f(0) = 1 \)
(2) \( f(1) = 3 \)
(3) \( f(x) \) 可能為一次式
(4) \( f(x) \) 可能為 \( 4x^4 + 2x^2 – 3 \)
(5) \( f(x) \) 可能為 \( 4x^4 + 2x^3 – 3 \)。
設 \( f(x) = (x^2-1)Q(x) + (2x+1) \)。
(1) \( f(0) = -Q(0)+1 \) 不一定為1。
(2) \( f(1) = 0 + 3 = 3 \) ✓。
(3) 若 \( Q(x)=0 \),則 \( f(x)=2x+1 \) 為一次式 ✓。
(4) 計算 \( (4x^4+2x^2-3) - (2x+1) = 4x^4+2x^2-2x-4 \),除以 \( x^2-1 \) 不整除 ✗。
(5) 計算 \( (4x^4+2x^3-3) - (2x+1) = 4x^4+2x^3-2x-4 \),可被 \( x^2-1 \) 整除 ✓。
故選(2)(3)(5)。答案:(2)(3)(5) 報錯
ChatGPT DeepSeek
107學測數學考科-10
已知坐標平面上 \(\triangle ABC\),其中 \(\overset{\rightharpoonup}{AB} = (-4,3)\),且 \(\overset{\rightharpoonup}{AC} = \left( \frac{2}{5}, \frac{4}{5} \right)\)。試選出正確的選項。
(1) \(\overline{BC} = 5\)
(2) \(\triangle ABC\) 是直角三角形
(3) \(\triangle ABC\) 的面積為 \(\frac{11}{5}\)
(4) \(\sin B \gt \sin C\)
(5) \(\cos A \gt \cos B\)。
(1) \( \overset{\rightharpoonup}{BC} = \overset{\rightharpoonup}{AC} - \overset{\rightharpoonup}{AB} = \left( \frac{22}{5}, -\frac{11}{5} \right) \),長度 \( \frac{11\sqrt{5}}{5} \neq 5 \) ✗。
(2) \( \overline{AB}=5 \),\( \overline{AC}=\frac{2\sqrt{5}}{5} \),\( \overline{BC}=\frac{11\sqrt{5}}{5} \),檢查得 \( \overline{AC}^2 + \overline{BC}^2 = \frac{4}{5} + \frac{121}{5} = 25 = \overline{AB}^2 \) ✓。
(3) 面積 \( \frac{1}{2} \times \frac{2\sqrt{5}}{5} \times \frac{11\sqrt{5}}{5} = \frac{11}{5} \) ✓。
(4) \( \sin B = \frac{\overline{AC}}{\overline{AB}} = \frac{2\sqrt{5}}{25} \),\( \sin C = 1 \),故 \( \sin B \lt \sin C \) ✗。
(5) \( \cos A = \frac{\overset{\rightharpoonup}{AB} \cdot \overset{\rightharpoonup}{AC}}{5 \cdot \frac{2\sqrt{5}}{5}} = \frac{-8/5+12/5}{2\sqrt{5}} = \frac{4/5}{2\sqrt{5}} = \frac{2}{5\sqrt{5}} \),\( \cos B = \frac{\overset{\rightharpoonup}{BA} \cdot \overset{\rightharpoonup}{BC}}{5 \cdot \frac{11\sqrt{5}}{5}} = \frac{ (4,-3) \cdot (22/5,-11/5) }{11\sqrt{5}} = \frac{88/5+33/5}{11\sqrt{5}} = \frac{121/5}{11\sqrt{5}} = \frac{11}{5\sqrt{5}} \),故 \( \cos A \lt \cos B \) ✗。
故選(2)(3)。答案:(2)(3) 報錯
ChatGPT DeepSeek