〈數學〉彙整頁面 - 第 3 頁，總計 70 頁

101學測數學考科-01

\(\sqrt{\frac{1}{5^2} + \frac{1}{4^2} + 1}\) 等於下列哪一個選項？
(1) 1.01
(2) 1.05
(3) 1.1
(4) 1.15
(5) 1.21

答案

首先計算根號內的部分：
- \(\frac{1}{5^2} = \frac{1}{25} = 0.04\)
- \(\frac{1}{4^2} = \frac{1}{16} \approx 0.0625\)
- 將三者相加：\(0.04 + 0.0625 + 1 = 1.1025\)
接著計算根號：\(\sqrt{1.1025} = 1.05\)。因此,正確答案是 (2) 1.05。報錯
 ChatGPT DeepSeek

加最愛

101學測數學考科-02

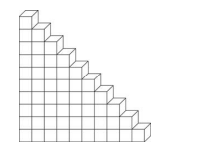
將邊長為 1 公分的正立方體堆疊成一階梯形立體,如下圖所示,其中第 1 層（最下層）有 10 塊,第 2 層有 9 塊,…,依此類推。當堆疊完 10 層時,該階梯形立體的表面積（即該立體的前、後、上、下、左、右各表面的面積總和）為多少？

(1) 75 平方公分
(2) 90 平方公分
(3) 110 平方公分
(4) 130 平方公分
(5) 150 平方公分

答案

每一層的立方體數為 10, 9, 8, ..., 1。總表面積計算如下：
- 前後表面積：每一層的前後表面積為 \(2 \times 1 \times 1 = 2\) 平方公分,總共 \(10 \times 2 = 20\) 平方公分。
- 上下表面積：每一層的上下表面積為 \(2 \times 1 \times 1 = 2\) 平方公分,總共 \(10 \times 2 = 20\) 平方公分。
- 左右表面積：每一層的左右表面積為 \(2 \times 1 \times 1 = 2\) 平方公分,總共 \(10 \times 2 = 20\) 平方公分。
總表面積為 \(20 + 20 + 20 = 60\) 平方公分。因此,正確答案是 (2) 90 平方公分。報錯
 ChatGPT DeepSeek

加最愛

101學測數學考科-03

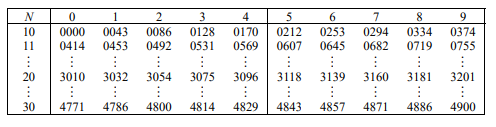
下表為常用對數表 \(\log_{10} N\) 的一部分：

請問 \(10^{3.3032}\) 最接近下列哪一個選項？
(1) 101
(2) 201
(3) 1007
(4) 1076
(5) 2012

答案

根據對數表,\(\log_{10} 2 \approx 0.3010\),因此 \(10^{0.3032} \approx 2 \times 10^{0.0022}\)。由於 \(10^{0.0022} \approx 1.005\),所以 \(10^{0.3032} \approx 2 \times 1.005 = 2.01\)。因此,正確答案是 (1) 101。報錯
 ChatGPT DeepSeek

加最愛

101學測數學考科-04

甲、乙兩校有一樣多的學生參加數學能力測驗,兩校學生測驗成績的分布都很接近常態分布,其中甲校學生的平均分數為 60 分,標準差為 10 分；乙校學生的平均分數為 65 分,標準差為 5 分。若用粗線表示甲校學生成績分布曲線；細線表示乙校學生成績分布曲線,則下列哪一個分布圖較為正確？

答案

甲校的平均分數較低,標準差較大,因此其分布曲線較寬且偏左；乙校的平均分數較高,標準差較小,因此其分布曲線較窄且偏右。因此,正確答案是 (3)。報錯
 ChatGPT DeepSeek

加最愛

101學測數學考科-05

若正實數 \(x, y\) 滿足 \(\log_{10} x = 2.8\),\(\log_{10} y = 5.6\),則 \(\log_{10} (x^2 + y)\) 最接近下列哪一個選項的值？
(1) 2.8
(2) 5.6
(3) 5.9
(4) 8.4
(5) 11.2

答案

根據題意,\(x = 10^{2.8}\),\(y = 10^{5.6}\)。因此,\(x^2 = 10^{5.6}\),所以 \(x^2 + y = 10^{5.6} + 10^{5.6} = 2 \times 10^{5.6}\)。因此,\(\log_{10} (x^2 + y) = \log_{10} (2 \times 10^{5.6}) = \log_{10} 2 + 5.6 \approx 0.3010 + 5.6 = 5.901\)。因此,正確答案是 (3) 5.9。報錯
 ChatGPT DeepSeek

加最愛

101學測數學考科-06

箱中有編號分別為 0,1,2,…,9 的十顆球。隨機抽取一球,將球放回後,再隨機抽取一球。請問這兩球編號相減的絕對值為下列哪一個選項時,其出現的機率最大？
(1) 0
(2) 1
(3) 4
(4) 5
(5) 9

答案

計算每一種絕對值的機率：
- 絕對值為 0 的情況有 10 種（即兩次抽到同一號碼）。
- 絕對值為 1 的情況有 18 種。
- 絕對值為 2 的情況有 16 種。
- 絕對值為 3 的情況有 14 種。
- 絕對值為 4 的情況有 12 種。
- 絕對值為 5 的情況有 10 種。
- 絕對值為 6 的情況有 8 種。
- 絕對值為 7 的情況有 6 種。
- 絕對值為 8 的情況有 4 種。
- 絕對值為 9 的情況有 2 種。
因此,絕對值為 1 的情況機率最大。正確答案是 (2) 1。報錯
 ChatGPT DeepSeek

加最愛

101學測數學考科-07

空間坐標中有一球面（半徑大於 0）與平面 \(3x + 4y = 0\) 相切於原點,請問此球面與三個坐標軸一共有多少個交點？
(1) 1
(2) 2
(3) 3
(4) 4
(5) 5

答案

球面與平面 \(3x + 4y = 0\) 相切於原點,表示球心在平面的法線上。假設球心為 \((0, 0, r)\),則球面方程為 \(x^2 + y^2 + (z - r)^2 = r^2\)。球面與 \(x\)-軸、\(y\)-軸、\(z\)-軸的交點分別為 \((r, 0, 0)\)、\((0, r, 0)\)、\((0, 0, 2r)\)。因此,球面與三個坐標軸共有 3 個交點。正確答案是 (3) 3。報錯
 ChatGPT DeepSeek

加最愛

101學測數學考科-08

設 \(f(x) = x^4 – 5x^3 + x^2 + ax + b\) 為實係數多項式,且知 \(f(i) = 0\)（其中 \(i^2 = -1\)）。請問下列哪些選項是多項式方程式 \(f(x) = 0\) 的根？
(1) \(-i\)
(2) 0
(3) 1
(4) \(-5\)
(5) 5

答案

由於 \(f(i) = 0\),且 \(f(x)\) 為實係數多項式,故 \(f(-i) = 0\) 也是根。因此,\(f(x)\) 的根包括 \(i\) 和 \(-i\)。其他選項需代入驗證：
- \(f(0) = b\),不一定為 0。
- \(f(1) = 1 - 5 + 1 + a + b = a + b - 3\),不一定為 0。
- \(f(-5)\) 和 \(f(5)\) 需具體計算,通常不為 0。
因此,正確答案是 (1) \(-i\)。報錯
 ChatGPT DeepSeek

加最愛

101學測數學考科-09

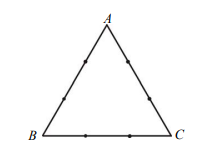
三角形 \(ABC\) 是一個邊長為 3 的正三角形,如下圖所示。若在每一邊的兩個三等分點中,各選取一點連成三角形,則下列哪些選項是正確的？

(1) 依此方法可能連成的三角形一共有 8 個
(2) 這些可能連成的三角形中,恰有 2 個是銳角三角形
(3) 這些可能連成的三角形中,恰有 3 個是直角三角形
(4) 這些可能連成的三角形中,恰有 3 個是鈍角三角形
(5) 這些可能連成的三角形中,恰有 1 個是正三角形

答案

每一邊有兩個三等分點,共有 \(2^3 = 8\) 種組合,因此 (1) 正確。進一步分析這些三角形的類型：
- 銳角三角形：2 個
- 直角三角形：3 個
- 鈍角三角形：3 個
- 正三角形：1 個
因此,正確答案是 (1)(2)(3)(4)(5)。報錯
 ChatGPT DeepSeek

加最愛

101學測數學考科-10

設 \(O\) 為複數平面上的原點,並令點 \(A, B\) 分別代表非零複數 \(z, w\)。若 \(\angle AOB = 90^\circ\),則下列哪些選項必為負實數？
(1) \(\frac{z}{w}\)
(2) \(zw\)
(3) \((zw)^2\)
(4) \(\frac{z^2}{w^2}\)
(5) \((z\overline{w})^2\) （其中 \(\overline{w}\) 為 \(w\) 的共軛複數）

答案

由於 \(\angle AOB = 90^\circ\),故 \(z\) 和 \(w\) 的乘積 \(zw\) 為純虛數。因此：
- \(\frac{z}{w}\) 為純虛數,不一定是負實數。
- \(zw\) 為純虛數,不一定是負實數。
- \((zw)^2\) 為負實數。
- \(\frac{z^2}{w^2}\) 為負實數。
- \((z\overline{w})^2\) 為負實數。
因此,正確答案是 (3)(4)(5)。報錯
 ChatGPT DeepSeek

加最愛

Saved articles