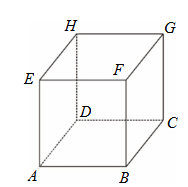
坐標空間中有一個正立方體ABCDEFGH ,承(3),試求出G點的坐標。(4分)
[非選擇題]由(2)知\(\overrightarrow{AG}\)與平面BDE垂直,所以\(\overrightarrow{AG}\)平行於平面BDE的法向量\(\overrightarrow{n}=(2,2,-1)\)(平面2x + 2y - z = -7的法向量)。
設G點坐標為\((x,y,z)\),則\(\overrightarrow{AG}=(x - 2,y - 2,z - 6)\)。
因為\(\overrightarrow{AG}\)與\(\overrightarrow{n}=(2,2,-1)\)平行,所以\(\frac{x - 2}{2}=\frac{y - 2}{2}=\frac{z - 6}{-1}=k\)(k為常數),即\(x = 2k + 2\),\(y = 2k + 2\),\(z = -k + 6\)。
又由(3)知A點到平面BDE的距離是3,且G點到平面BDE的距離與A點到平面BDE的距離相等(正立方體性質)。
將G點坐標\((2k + 2,2k + 2,-k + 6)\)代入點到平面的距離公式\(d=\frac{\vert2(2k + 2)+2(2k + 2)-(-k + 6)+7\vert}{\sqrt{2^{2}+2^{2}+(-1)^{2}}}=3\)。
\(\frac{\vert4k + 4 + 4k + 4 + k - 6 + 7\vert}{3}=3\),\(\vert9k + 9\vert = 9\),即\(9k + 9 = 9\)或\(9k + 9 = -9\)。
解得\(k = 0\)或\(k = -2\),\(k = 0\)時不滿足G與A不重合,所以\(k = -2\)。
則\(x = 2\times(-2)+2=-2\),\(y = 2\times(-2)+2=-2\),\(z = -(-2)+6 = 8\)。
所以G點坐標為(-2,-2,8)。 報錯
ChatGPT DeepSeek