有一積木,其中\(ACFD\)和\(ABED\)是兩個全等的等腰梯形,\(BCFE\)是一個矩形。設\(A\)點在直線\(BC\)的投影為\(M\)且在平面\(BCFE\)的投影為\(P\)。已知\(\overline{AD}=30\) ,\(\overline{CF}=40\) ,\(\overline{AP}=15\)且\(\overline{BC}=10\) 。將平面\(BCFE\)置於水平桌面上,且將與\(BCFE\)平行的平面稱為水平面。利用\(\overline{AD}\)在平面\(BCFE\)的投影長為\(30\),可得\(\tan\angle AMP = \)__________ 。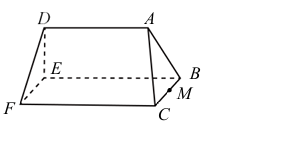
數學
111分科數學甲試題-13
有一積木,其中\(ACFD\)和\(ABED\)是兩個全等的等腰梯形,\(BCFE\)是一個矩形。設\(A\)點在直線\(BC\)的投影為\(M\)且在平面\(BCFE\)的投影為\(P\)。已知\(\overline{AD}=30\) ,\(\overline{CF}=40\) ,\(\overline{AP}=15\)且\(\overline{BC}=10\) 。令\(Q\)為\(\overline{FC}\)上一點,滿足\(\overrightarrow{AQ}\)與\(\overrightarrow{DF}\)平行。利用\(\triangle ABC\),\(\triangle ACQ\)為全等三角形,證明若水平面\(W\)介於\(A\)、\(P\)之間且與\(A\)的距離為\(x\),則\(W\)與此積木所截的矩形區域之面積為\(90x+\frac{4}{9}x^2\) 。
[非選擇]證明:由\(\triangle ABC\cong\triangle ACQ\)可得\(CQ = BC = 10\)。過\(A\)作\(AH\perp FC\)於\(H\),可得\(FH = 15\) 。因為\(\triangle AFH\)與截面相似,相似比為\(\frac{15 - x}{15}\)。設截面矩形長為\(l\),寬為\(w\),由相似比可得\(\frac{l}{40}=\frac{15 - x}{15}\),\(l=\frac{40(15 - x)}{15}=\frac{8(15 - x)}{3}\);同理可得\(\frac{w}{10}=\frac{15 - x}{15}\) ,\(w=\frac{10(15 - x)}{15}=\frac{2(15 - x)}{3}\)。截面面積\(S = lw\) ,代入化簡可得\(S = 20x+\frac{4}{9}x^{2}\) 。 報錯
ChatGPT DeepSeek
111分科數學甲試題-14
有一積木,其中\(ACFD\)和\(ABED\)是兩個全等的等腰梯形,\(BCFE\)是一個矩形。設\(A\)點在直線\(BC\)的投影為\(M\)且在平面\(BCFE\)的投影為\(P\)。已知\(\overline{AD}=30\) ,\(\overline{CF}=40\) ,\(\overline{AP}=15\)且\(\overline{BC}=10\) 。將線段\(\overline{AP}\)的\(n\)等分點沿著向量\(\overrightarrow{AP}\)的方向依序設為\(A = P_{0},P_{1},\cdots,P_{n – 1},P_{n}=P\) 。在每一個分段\(\overline{P_{k – 1}P_{k}}\) ,考慮以通過\(P_{k}\)的水平面與此積木所截的矩形為底、\(\overline{P_{k – 1}P_{k}}\)為高,所形成的長方體。請利用此切片方法寫下估計此積木體積的黎曼和(不需化簡),且以定積分形式表示此積木的體積並求其值。
[非選擇]黎曼和:\(\sum_{k = 1}^{n}(20\frac{15(k - 1)}{n}+\frac{4}{9}(\frac{15(k - 1)}{n})^{2})\frac{15}{n}\)。定積分形式:\(V=\int_{0}^{15}(20x+\frac{4}{9}x^{2})dx\) 。計算定積分:\(\int_{0}^{15}(20x+\frac{4}{9}x^{2})dx=(10x^{2}+\frac{4}{27}x^{3})\big|_{0}^{15}=10\times15^{2}+\frac{4}{27}\times15^{3}=2250 + 500 = 2750\) ,所以積木體積為\(2750\) 。 報錯
ChatGPT DeepSeek
111分科數學甲試題-15~17
考慮坐標平面上之向量\(\overrightarrow{a}\)、\(\overrightarrow{b}\)滿足\(|\overrightarrow{a}| + |\overrightarrow{b}| = 9\)以及\(|\overrightarrow{a} – \overrightarrow{b}| = 7\)。若令\(|\overrightarrow{a}| = x\),其中\(1 \lt x \lt 8\),且令\(\overrightarrow{a}\)、\(\overrightarrow{b}\)的夾角為\(\theta\),則利用向量\(\overrightarrow{a}\)、\(\overrightarrow{b}\)、\(\overrightarrow{a} – \overrightarrow{b}\)所形成的三角形,可將\(\cos\theta\)以x表示成\(\frac{c}{9x – x^2} + d\),其中c、d為常數且\(c \gt 0\)。令此表示式為\(f(x)\),且其定義域為\(\{x \mid 1 \lt x \lt 8\}\)。試回答下列問題:
15.求\(f(x)\)及其導函數。
16.說明\(f(x)\)在定義域中遞增、遞減的情況。並說明x為多少時\(\overrightarrow{a}\)、\(\overrightarrow{b}\)的夾角\(\theta\)最大。
17.利用\(f(x)\)的一次估計(一次近似),求當\(x = 4.96\)時,\(\cos\theta\)約為多少?
15. 求\(f(x)\)及其導函數已知\(|\vec{a}| = x\),則\(|\vec{b}| = 9 - x\)。由\(|\vec{a} - \vec{b}| = 7\),根據向量模長公式:\(7^2 = x^2 + (9 - x)^2 - 2x(9 - x)\cos\theta\)
展開整理得:\(49 = 2x^2 - 18x + 81 - 2x(9 - x)\cos\theta \implies \cos\theta = \frac{16}{9x - x^2} - 1\)
故\(f(x) = \frac{16}{9x - x^2} - 1\)。求導:\(f'(x) = \frac{16 \cdot (2x - 9)}{(9x - x^2)^2} = \frac{32x - 144}{(9x - x^2)^2}\)16. \(f(x)\)的單調性與\(\theta\)最大值當\(1 < x < 4.5\),\(f'(x) < 0\),\(f(x)\)遞減;當\(4.5 < x < 8\),\(f'(x) > 0\),\(f(x)\)遞增。\(\cos\theta\)越小,\(\theta\)越大。\(f(x)\)在\(x = 4.5\)時取最小值,此時\(\cos\theta\)最小,故\(x = 4.5\)時,\(\theta\)最大。17. 一次估計求\(\cos\theta\)取\(x_0 = 5\),計算:\(f(5) = \frac{16}{25} - 1 = -0.2, \quad f'(5) = \frac{16}{400} = 0.04\)
當\(x = 4.96\),\(\Delta x = -0.04\),線性近似:\(f(4.96) \approx f(5) + f'(5) \cdot (-0.04) = -0.2 - 0.0016 = -0.2016\) 報錯
ChatGPT DeepSeek
03-113分科測驗數學甲試題16
坐 標 平 面 上,設 \( \Gamma \) 為 三 次 函 數 \( f(x)=x^{3}-9x^{2}+15x – 4\) 的 函 數 圖 形。試 說明 \( P(1,3)\) 為 \( \Gamma \) 上 之 一 點,並 求 \( \Gamma \) 在 \( P\) 點的 切線 \( L\) 的 方程式。
[非選擇]04 – 114學測數學b試題01
設數線上有一點\(P\)滿足\(P\)到\(1\)的距離加上\(P\)到\(4\)的距離等於\(4\)。試問這樣的\(P\)有幾個?(1) \(0\)個;(2) \(1\)個;(3) \(2\)個;(4) \(3\)個;(5) 無限多個
[單選]設點\(P\)表示的數為\(x\),則\(\vert x - 1\vert + \vert x - 4\vert = 4\)。當\(x \leq 1\)時,\(1 - x + 4 - x = 4\),解得\(x = \frac{1}{2}\);當\(1 < x < 4\)時,\(x - 1 + 4 - x = 3 \neq 4\),無解;當\(x \geq 4\)時,\(x - 1 + x - 4 = 4\),解得\(x = \frac{9}{2}\)。所以這樣的\(P\)有\(2\)個。答案:(3) 報錯
ChatGPT DeepSeek
https://www.ceec.edu.tw/files/file_pool/1/0n045358876595832120/03-112%e5%ad%b8%e6%b8%ac%e6%95%b8%e5%ad%b8a%e9%81%b8%e6%93%87%28%e5%a1%ab%29%e9%a1%8c%e7%ad%94%e6%a1%88.pdf
04 – 114學測數學b試題02
設 \( A \) 為 \( 3 \times 2 \) 階矩陣,且 \( A\begin{bmatrix} 1 & 0 \\ -1 & 1 \end{bmatrix} = \begin{bmatrix} 4 & -6 \\ -2 & 1 \\ 3 & 5 \end{bmatrix} \)。若 \( A\begin{bmatrix} 1 \\ 0 \end{bmatrix} = \begin{bmatrix} a \\ b \\ c \end{bmatrix} \),試問 \( a + b + c \) 之值為何?
(1) 0
(2) 2
(3) 4
(4) 5
(5) 8
1. 設 \( A = \begin{bmatrix} m & n \\ p & q \\ r & s \end{bmatrix} \),計算 \( A\begin{bmatrix} 1 & 0 \\ -1 & 1 \end{bmatrix} \):
\[
\begin{bmatrix} m - n & n \\ p - q & q \\ r - s & s \end{bmatrix} = \begin{bmatrix} 4 & -6 \\ -2 & 1 \\ 3 & 5 \end{bmatrix}
\]
2. 對應元素相等,得:
- \( m - n = 4 \),\( n = -6 \implies m = 4 + (-6) = -2 \)
- \( p - q = -2 \),\( q = 1 \implies p = -2 + 1 = -1 \)
- \( r - s = 3 \),\( s = 5 \implies r = 3 + 5 = 8 \)
3. 計算 \( A\begin{bmatrix} 1 \\ 0 \end{bmatrix} = \begin{bmatrix} m \\ p \\ r \end{bmatrix} = \begin{bmatrix} -2 \\ -1 \\ 8 \end{bmatrix} \),即 \( a = -2 \),\( b = -1 \),\( c = 8 \)
4. 求和:\( a + b + c = -2 + (-1) + 8 = 5 \),故答案為(4)。 報錯
ChatGPT DeepSeek
https://www.ceec.edu.tw/files/file_pool/1/0p051541901400830673/04-114%e5%ad%b8%e6%b8%ac%e6%95%b8%e5%ad%b8b%e7%ad%94%e6%a1%88.pdf
04 – 114學測數學b試題03
已知實數 \( a,b \) 滿足 \( \frac{1}{2} \lt a \lt 1 \) 及 \( 1 \lt b \lt 2 \)。試問下列哪個選項的值最小?
(1) 0
(2) \( \log a \)
(3) \( \log(a^2) \)
(4) \( \log b \)
(5) \( \frac{1}{\log b} \)
1. 分析選項(2):
因 \( \frac{1}{2} < a < 1 \),對數函數 \( y = \log x \)(以10或自然對數為底,底數>1)在\( (0,1) \)上為負,故 \( \log a < 0 \)。
2. 分析選項(3):
\( \log(a^2) = 2\log a \),因 \( \log a < 0 \),故 \( 2\log a < \log a \)(負數乘以2更小)。
3. 分析選項(4):
因 \( 1 < b < 2 \),故 \( \log b > 0 \)。
4. 分析選項(5):
因 \( \log b > 0 \),故 \( \frac{1}{\log b} > 0 \)。
5. 比較選項(2)與(3):
令 \( a = \frac{\sqrt{2}}{2} \)(滿足 \( \frac{1}{2} < a < 1 \)),則 \( \log a = \log \frac{\sqrt{2}}{2} = \frac{1}{2}\log 2 - \log 2 = -\frac{1}{2}\log 2 \),\( \log(a^2) = 2 \times (-\frac{1}{2}\log 2) = -\log 2 \)。
因 \( -\log 2 < -\frac{1}{2}\log 2 \),故 \( \log(a^2) < \log a \)。
综上,選項(3)的值最小。" 報錯
ChatGPT DeepSeek
https://www.ceec.edu.tw/files/file_pool/1/0p051541901400830673/04-114%e5%ad%b8%e6%b8%ac%e6%95%b8%e5%ad%b8b%e7%ad%94%e6%a1%88.pdf
04 – 114學測數學b試題04
某商店推出抽獎活動,提供香蕉、鳳梨、蘋果、橘子四種不同款式的水果公仔當獎品。每次抽獎可得1個公仔,且每種款式被抽中的機率皆相等。某甲決定抽獎四次,試問他恰抽到三種不同款式公仔的機率為何?
(1) \(\frac{5}{16}\)
(2) \(\frac{3}{8}\)
(3) \(\frac{1}{2}\)
(4) \(\frac{9}{16}\)
(5) \(\frac{5}{8}\)
1. 計算所有可能的抽獎結果:
每次抽獎有4種選擇,抽4次的總結果數為 \(4^4 = 256\)。
2. 計算「恰抽到三種不同款式」的結果數:
- 第一步:選擇哪3種款式,組合數為 \(C(4,3) = 4\)。
- 第二步:在4次抽獎中,其中一種款式抽2次,另外兩種各抽1次。
- 選擇哪種款式抽2次:3種選擇。
- 安排這2次的位置:\(C(4,2) = 6\)。
- 剩下2次分配給另外兩種款式:\(2! = 2\) 種排列。
- 因此,符合條件的結果數為 \(4 \times 3 \times 6 \times 2 = 144\)。
3. 計算機率:
機率 = 符合條件的結果數 / 總結果數 = \(\frac{144}{256} = \frac{9}{16}\),故答案為(4)。 報錯
ChatGPT DeepSeek
https://www.ceec.edu.tw/files/file_pool/1/0p051541901400830673/04-114%e5%ad%b8%e6%b8%ac%e6%95%b8%e5%ad%b8b%e7%ad%94%e6%a1%88.pdf
04 – 114學測數學b試題05
空間中有兩相交直線\(L\),\(M\),其夾角為\(24^{\circ}\)。將\(M\)繞著\(L\)轉一圈,可得一個直圓錐面。今有平面\(E\)與直線\(L\)平行,試問平面\(E\)與此直圓錐面的截痕是下列哪一個選項?(1) 雙曲線;(2) 拋物線;(3) 橢圓(長短軸不相等);(4) 圓;(5) 兩相交直線
[單選]1. **圓錐面性質**:直線\(M\)繞\(L\)旋轉形成直圓錐面,錐角為\(24^\circ\)。
2. **平面與圓錐面的截痕**:平面\(E\)與直線\(L\)平行,且不通過圓錐頂點。
3. **結果**:根據圓錐截痕的性質,當平面與軸平行且不與母線平行時,截痕為**雙曲線**。
**答案**:(1) 雙曲線。
https://www.ceec.edu.tw/files/file_pool/1/0p051541901400830673/04-114%e5%ad%b8%e6%b8%ac%e6%95%b8%e5%ad%b8b%e7%ad%94%e6%a1%88.pdf

