 聖誕樹燈飾相似三角形題”,”某大樓居民在大樓外牆展示聖誕樹造型燈飾,如圖所示,從五樓外牆某處\( P \)向四樓地板的兩端\( A,B \)拉小燈泡形成等腰三角形\( PAB \),其中\( PA=PB \);向三樓地板的兩端\( C,D \)拉小燈泡形成等腰三角形\( PCD \);向二樓地板的兩端\( E,F \)拉小燈泡形成等腰三角形\( PEF \)。假設每層樓等高且樓地板長度相等,若五樓地板在三角形\( PAB \)內部所截出的線段長度為樓地板長度的\( \frac{1}{3} \),則五樓地板在三角形\( PEF \)內部所截出的線段長度是樓地板長度的幾分之幾?(燈飾粗細可忽略不計)
聖誕樹燈飾相似三角形題”,”某大樓居民在大樓外牆展示聖誕樹造型燈飾,如圖所示,從五樓外牆某處\( P \)向四樓地板的兩端\( A,B \)拉小燈泡形成等腰三角形\( PAB \),其中\( PA=PB \);向三樓地板的兩端\( C,D \)拉小燈泡形成等腰三角形\( PCD \);向二樓地板的兩端\( E,F \)拉小燈泡形成等腰三角形\( PEF \)。假設每層樓等高且樓地板長度相等,若五樓地板在三角形\( PAB \)內部所截出的線段長度為樓地板長度的\( \frac{1}{3} \),則五樓地板在三角形\( PEF \)內部所截出的線段長度是樓地板長度的幾分之幾?(燈飾粗細可忽略不計)
(1) \( \frac{1}{7} \)
(2) \( \frac{1}{6} \)
(3) \( \frac{1}{5} \)
(4) \( \frac{1}{9} \)
(5) \( \frac{1}{4} \)
數學
113學測數學B試題-07
有一城市分為東、西兩區。兩區各有一個氣溫偵測站,該城市當天的最高溫 (單 位:攝氏度) 是取這兩區當天氣溫的最大值來記錄。下表顯示東、西兩區某月(共30天)每日最高溫分布的情形。
| 溫度\(t\) | \(18\leq t\lt24\) | \(24\leq t\lt30\) | \(30\leq t\lt36\) | \(36\leq t\) |
| 東區(天數) | 0 | 11 | 14 | 5 |
| 西區(天數) | 3 | 12 | 15 | 0 |
根據上表,該城市當月每日最高溫分布的情形如下表。
| 溫度\(t\) | \(18\leq t\lt24\) | \(24\leq t\lt30\) | \(30\leq t\lt36\) | \(36\leq t\) |
| 天數 | \(A\) | \(B\) | \(C\) | \(D\) |
試選出有可能為數組\((A,B,C,D)\)的選項。(1) \((0,15,15,0)\);(2) \((3,12,15,5)\);(3) \((0,9,16,5)\);(4) \((3,7,15,5)\);(5) \((0,12,13,5)\)
[單選]113學測數學B試題-08
已知正實數數列\(a\),\(b\),\(c\),\(d\),\(e\)為等比數列,且\(a\lt b\lt c\lt d\lt e\),試選出下列為等比數列的選項。(1) \(a\),\(-b\),\(c\),\(-d\),\(e\);(2) \(e\),\(d\),\(c\),\(b\),\(a\);(3) \(\log a\),\(\log b\),\(\log c\),\(\log d\),\(\log e\);(4) \(3^a\),\(3^b\),\(3^c\),\(3^d\),\(3^e\);(5) \(abc\),\(bcd\),\(cde\)
[多選]1. 設原等比數列公比為\(q\),\(q\gt1\)。
- (1):是等比數列。
- (2):\(\frac{d}{e}=\frac{1}{q}\),\(\frac{c}{d}=\frac{1}{q}\),\(\frac{b}{c}=\frac{1}{q}\),\(\frac{a}{b}=\frac{1}{q}\),是等比數列。
- (3):\(\log b-\log a=\log\frac{b}{a}\),\(\log c-\log b=\log\frac{c}{b}\),若\(\log\frac{b}{a}=\log\frac{c}{b}\),則\(\frac{b}{a}=\frac{c}{b}\),原數列是等比數列,所以\(\log a\),\(\log b\),\(\log c\),\(\log d\),\(\log e\)是等差數列,不是等比數列。
- (4):\(\frac{3^b}{3^a}=3^{b - a}\),\(\frac{3^c}{3^b}=3^{c - b}\),\(b - a\neq c - b\),不是等比數列。
- (5):\(\frac{bcd}{abc}=\frac{d}{a}=q^3\),\(\frac{cde}{bcd}=\frac{e}{b}=q^3\),是等比數列。答案:(1)(2)(5) 報錯
ChatGPT DeepSeek
113學測數學B試題-09
已知多項式\(f(x)\)除以\(x^{2}+5x + 1\)後,所得出的商式為\(x^{3}+7x^{2}+x + 3\),試選出下列可能為\(f(x)\)的選項。(1) \(2(x^{3}+7x^{2}+x + 3)(x^{2}+5x + 1)\);(2) \((x^{3}+7x^{2}+x + 3)(x^{2}+5x + 1)-x\);(3) \((x^{3}+7x^{2}+x + 3)(x^{2}+5x + 1)+x^{2}\);(4) \((x^{3}+7x^{2}+x + 4)(x^{2}+5x + 1)-x\);(5) \((x^{3}+7x^{2}+x + 4)(x^{2}+5x + 1)-x^{2}\)
[多選]我們已知:
\[
f(x) = (x^2 + 5x + 1)(x^3 + 7x^2 + x + 3) + r(x),
\]
其中 \( r(x) \) 是餘式,且 \(\deg r(x) < 2\)。
所以 \( r(x) = ax + b \),其中 \( a, b \) 是常數。
---
**檢查選項:**
(1) \( 2(x^3 + 7x^2 + x + 3)(x^2 + 5x + 1) \)
這相當於 \( f(x) = 2Q(x)D(x) \),商式是 \( 2Q(x) \),不是 \( Q(x) \),不符合題目給的商式。 ❌
---
(2) \( (x^3 + 7x^2 + x + 3)(x^2 + 5x + 1) - x \)
這相當於 \( f(x) = Q(x)D(x) - x \),商式 \( Q(x) \),餘式 \( -x \),符合條件。 ✅
---
(3) \( (x^3 + 7x^2 + x + 3)(x^2 + 5x + 1) + x^2 \)
餘式 \( x^2 \),但 \(\deg x^2 = 2\),不滿足餘式次數 < 2,所以商式會改變。 ❌
---
(4) \( (x^3 + 7x^2 + x + 4)(x^2 + 5x + 1) - x \)
設 \( Q_1(x) = x^3 + 7x^2 + x + 4 \),比題目給的商式 \( Q(x) \) 多 1(常數項差 1)。
\[
f(x) = Q_1(x)D(x) - x = [Q(x) + 1]D(x) - x
= Q(x)D(x) + D(x) - x.
\]
這相當於商式 \( Q(x) \),餘式 \( D(x) - x = (x^2 + 5x + 1) - x = x^2 + 4x + 1 \),次數 2,不行。 ❌
---
(5) \( (x^3 + 7x^2 + x + 4)(x^2 + 5x + 1) - x^2 \)
\[
f(x) = [Q(x) + 1]D(x) - x^2
= Q(x)D(x) + D(x) - x^2
= Q(x)D(x) + (x^2 + 5x + 1 - x^2)
= Q(x)D(x) + (5x + 1).
\]
餘式 \( 5x + 1 \),次數 1,商式 \( Q(x) \),符合條件。 ✅
---
所以正確選項是 **(2)** 和 **(5)**。
---
**答案:** \(\boxed{2,5}\) 報錯
ChatGPT DeepSeek
113學測數學B試題-10
有兩個光點在一條長度為120公分的直線形軌道上移動,碰到端點就反向繼續移動。一開始兩點分別在軌道的兩端相向而動,光點\(A\)、光點\(B\)的移動速率分別為每秒5公分及每秒10公分。 試選出正確的選項。(1) 兩個光點第一次相遇的位置,與其中一個端點的距離為40公分;(2) 光點\(A\)的位置呈週期現象,週期為24秒;(3) 當光點\(A\)回到\(A\)的出發點時,光點\(B\)也在\(B\)的出發點;(4) 兩個光點第二次相遇在其中一個端點上;(5) 兩個光點在軌道上共有3個不同的相遇位置
[多選]我們先整理已知條件:
- 軌道長 \( L = 120 \) 公分
- A 從左端(位置 0)出發向右,速率 \( v_A = 5 \) cm/s
- B 從右端(位置 120)出發向左,速率 \( v_B = 10 \) cm/s
- 碰到端點就反向(彈性碰撞,速度反向)
---
## 1. 第一次相遇
初始相距 \( 120 \),相對速度 \( 5 + 10 = 15 \) cm/s
第一次相遇時間 \( t_1 = \frac{120}{15} = 8 \) 秒
A 移動 \( 5 \times 8 = 40 \) cm,從位置 0 到 40
B 移動 \( 10 \times 8 = 80 \) cm,從位置 120 到 40
所以第一次相遇在位置 40。
**(1)** 說「與其中一個端點的距離為 40 公分」
從左端 0 到 40 是 40 cm,從右端 120 到 40 是 80 cm,所以「與其中一個端點」的距離是 40 cm 沒錯。 ✅
---
## 2. A 的週期
A 從 0 到 120 需 \( \frac{120}{5} = 24 \) 秒,再從 120 回到 0 需 24 秒,所以回到原位置且速度方向相同(向右)的週期是 \( 48 \) 秒。
但題目 (2) 說「位置呈週期現象,週期為 24 秒」:
位置函數(不考慮方向)在反彈後會對稱,但從 0 到 120 再回到 0 的「位置圖」是三角波,半週期 24 秒回到原點但速度反向,全週期 48 秒才完全重複(位置與速度方向都相同)。
如果只考慮位置(不考慮速度方向),週期是 24 秒嗎?
檢查:
A 在 t=0 位置 0,t=24 位置 120,t=48 位置 0,所以位置函數 \( x_A(t) \) 滿足 \( x_A(t+24) = L - x_A(t) \),不是 \( x_A(t+24) = x_A(t) \),所以位置本身週期不是 24,而是 48。
因此 (2) ❌
---
## 3. A 回到出發點時 B 是否也在出發點
A 回到出發點(位置 0)的時間:
從 0 到 120 需 24 秒(在右端),再回到 0 需 48 秒(在左端),所以回到出發點的時間是 48 秒的整數倍: \( t = 48k \) 秒。
B 的運動:從 120 向左到 0 需 \( \frac{120}{10} = 12 \) 秒,再從 0 向右到 120 需 12 秒,所以 B 回到出發點(位置 120)的時間是 \( t = 24m \) 秒(因為每 24 秒回到右端一次)。
A 回到出發點的時間:48, 96, ...
B 回到出發點的時間:24, 48, 72, 96, ...
在 48 秒時,A 在 0(出發點),B 在 120(出發點)嗎?
檢查 B:
0–12 秒:B 從 120 到 0
12–24 秒:B 從 0 到 120(t=24 在 120)
24–36 秒:B 從 120 到 0
36–48 秒:B 從 0 到 120(t=48 在 120) ✅
所以 t=48 時兩者都在出發點。
**(3)** 說「當光點 A 回到 A 的出發點時,光點 B 也在 B 的出發點」
我們只驗證了 t=48 秒成立,但題目意思是「每次 A 回到出發點時,B 也在出發點」?
A 回到出發點時間:48k
B 回到出發點時間:24m
48k 必是 24 的倍數,所以 B 在端點,但不一定在「B 的出發點(120)」?
B 的出發點是 120,B 在端點有兩個:0 和 120。
B 在 t=24m 時在 120,在 t=12+24m 時在 0。
48k 是偶數個 24,所以 m 是偶數? 48k/24 = 2k 是偶數,所以 B 在 120。
所以確實每當 A 在 0 時,B 在 120。
因此 (3) ✅
---
## 4. 第二次相遇在端點?
第一次相遇在 t=8,位置 40。
之後兩者交換速度嗎?不,是實際的物體,不是交換速度的質點,所以各自繼續運動(但反向)。
第一次相遇後:
A 在 40 向右 5,B 在 40 向左 10。
B 先到左端 0:從 40 到 0 需 4 秒(B 向左 10 cm/s),此時 t=12。
A 從 40 向右走 4 秒到 60。
B 在 0 反彈向右 10,A 在 60 向右 5。
從 t=12 起:
A 在 60 向右 5,B 在 0 向右 10,B 追 A? 相對速度 5,距離 60,需 12 秒,在 t=24 時追上。
位置:B 從 0 向右 10×12=120,到 120(右端),A 從 60 向右 5×12=60,到 120。
所以第二次相遇在 t=24,位置 120(右端)。
**(4)** 說「第二次相遇在其中一個端點上」✅
---
## 5. 共有 3 個不同的相遇位置
第一次:位置 40
第二次:位置 120
第三次相遇:
第二次相遇在 t=24 位置 120 時,A 本來向右到右端 120,B 向左? 不對,檢查 t=24 時:
A 在 120 正要反彈向左 5,B 在 120 正要反彈向左? 不對,B 在 t=24 時從右端 120 反彈向左 10,所以兩者都在 120 反彈向左,但速度不同(A 向左 5,B 向左 10)。
所以第三次相遇:
t=24 後,B 速度 10 向左,A 速度 5 向左,B 在前面? 不對,位置相同,B 更快向左,所以 B 會在前面,那怎麼相遇?
其實它們在端點相遇後,B 較快向左,A 較慢向左,所以 B 在前面,不可能再相遇,除非 B 到左端反彈向右再追上 A。
我們改用相對運動分析:
在坐標系中,把反彈展開成直線運動(鏡像法):
A 的展開位置函數:\( X_A(t) = 5t \)(模 240 的三角波轉成直線 5t 再折回)
B 的展開位置函數:\( X_B(t) = 120 - 10t \)(模 240 的三角波)
相遇時 \( 5t \equiv 120 - 10t \pmod{240} \)
即 \( 15t \equiv 120 \pmod{240} \)
\( 15t = 120 + 240k \)
\( t = 8 + 16k \)
k=0: t=8(位置 40)
k=1: t=24(位置 120)
k=2: t=40(位置 40)
k=3: t=56(位置 120)
… 交替在 40 和 120 相遇。
所以只有 2 個不同相遇位置:40 和 120。
**(5)** 說「共有 3 個不同的相遇位置」❌
---
**正確選項:** (1)(3)(4)
---
**答案:** \(\boxed{1,3,4}\) 報錯
ChatGPT DeepSeek
113學測數學B試題-11
某國家過去五年的碳排放總量,由第1年的\(X\)億公噸二氧化碳當量(\(CO_2e\))下降至第5年的\(Y\)億公噸二氧化碳當量(\(CO_2e\)),達到每年平均減碳\(5\%\)的效益,亦即\(Y=(1 – 0.05)^4X\)。將五年的碳排放總量與年成長率記錄如下表,其中(第\(n\)年碳排放總量)−(第\(n – 1\)年碳排放總量)第\(n\)年碳排放成長率\(=\frac{(第n年碳排放總量)−(第n – 1年碳排放總量)}{第n – 1年碳排放總量}\),\(n = 2,3,4,5\)。
| 第1年 | 第2年 | 第3年 | 第4年 | 第5年 | |
| 碳排放總量(億公噸\(CO_2e\)) | \(X\) | \(A\) | \(B\) | \(C\) | \(Y\) |
| 碳排放年成長率 | \(-0.07\) | \(p\) | \(q\) | \(r\) |
試選出正確的選項。
(1) \(A = 0.93X\);
(2) \(Y\leq0.8X\);
(3) \(p\gt – 0.05\);
(4) \(r\gt – 0.05\);
(5) \(0.93(1 + p)(1 + q)(1 + r)=(0.95)^4\)
我們先整理已知條件:
- 第 1 年:\( X \)
- 第 5 年:\( Y \)
- 年均減碳 5%:\( Y = (1 - 0.05)^4 X = (0.95)^4 X \)
- 成長率定義:
\[
\text{第 } n \text{ 年成長率} = \frac{\text{第 } n \text{ 年碳排放總量} - \text{第 } n-1 \text{ 年碳排放總量}}{\text{第 } n-1 \text{ 年碳排放總量}}
\]
(題目公式分母寫 \( n \) 應為筆誤,應是前一年的量,否則單位不對。一般成長率 = (今年−去年)/去年。)
---
### (1) \( A = 0.93X \)
第 2 年成長率 = \( -0.07 \)
\[
\frac{A - X}{X} = -0.07 \implies A - X = -0.07X \implies A = 0.93X
\]
✅
---
### (2) \( Y \leq 0.8X \)
\( Y = (0.95)^4 X \)
\( 0.95^2 = 0.9025 \)
\( 0.95^4 = 0.9025^2 = 0.81450625 \)
所以 \( Y \approx 0.8145 X \),大於 \( 0.8X \)
因此 \( Y \leq 0.8X \) ❌
---
### (3) \[ \frac{-0.07 + p + q + r}{4} = -0.05 \]
這裡的「年均減碳 5%」是**複利年均成長率 (CAGR)**,不是算術平均年成長率。
CAGR = \( (Y/X)^{1/4} - 1 = -0.05 \)
算術平均年成長率 ≠ CAGR,除非每年成長率一樣。
所以此式不成立 ❌
---
### (4) \[ \sqrt[4]{\frac{Y}{X}} - 1 = -0.05 \]
這就是 CAGR 的定義,題目說 \( Y = (0.95)^4 X \),所以
\[
\sqrt[4]{\frac{Y}{X}} = 0.95 \implies \sqrt[4]{\frac{Y}{X}} - 1 = -0.05
\]
✅
---
### (5) \[ 0.93(1 + p)(1 + q)(1 + r) = (0.95)^4 \]
由成長率定義:
\( A = X(1 - 0.07) = 0.93X \)
\( B = A(1 + p) = 0.93X(1 + p) \)
\( C = B(1 + q) = 0.93X(1 + p)(1 + q) \)
\( Y = C(1 + r) = 0.93X(1 + p)(1 + q)(1 + r) \)
又 \( Y = (0.95)^4 X \)
所以
\[
0.93X(1 + p)(1 + q)(1 + r) = (0.95)^4 X
\]
\[
0.93(1 + p)(1 + q)(1 + r) = (0.95)^4
\]
✅
---
**正確選項:** (1), (4), (5)
---
**答案:** \(\boxed{1,4,5}\) 報錯
ChatGPT DeepSeek
113學測數學B試題-12
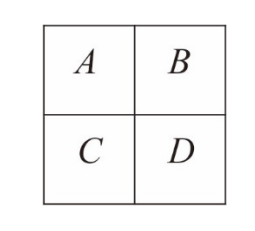 小明寫了一個程式讓機器人在\(2×2\)的棋盤中移動,如圖所示。每執行一次,程式會選擇「上、下、左、右」中的某一個方向,不同方向被選擇的機率均相等,並指示機器人依該方向移動一格,但若選到的方向會跑出棋盤,則機器人該次會停在原地。每次執行都是從上次所在位置依程式重新選取的方向移動,假設機器人的初始位置在\(A\)。 令執行程式\(n\)次後,機器人停留在\(A\)、\(B\)、\(C\)、\(D\)的機率分別為\(a_n\)、\(b_n\)、\(c_n\)和\(d_n\)。試選出正確的選項。
小明寫了一個程式讓機器人在\(2×2\)的棋盤中移動,如圖所示。每執行一次,程式會選擇「上、下、左、右」中的某一個方向,不同方向被選擇的機率均相等,並指示機器人依該方向移動一格,但若選到的方向會跑出棋盤,則機器人該次會停在原地。每次執行都是從上次所在位置依程式重新選取的方向移動,假設機器人的初始位置在\(A\)。 令執行程式\(n\)次後,機器人停留在\(A\)、\(B\)、\(C\)、\(D\)的機率分別為\(a_n\)、\(b_n\)、\(c_n\)和\(d_n\)。試選出正確的選項。
(1) \(b_1 = 0\);
(2) \(b_2=\frac{1}{8}\);
(3) \(a_2+d_2=\frac{3}{4}\);
(4) \(b_{99}=c_{99}\);
(5) \(a_{100} + d_{100} \gt\frac{ 1}{2}\)
我們一步步推理。
---
**1. 初始位置與一步轉移**
初始位置:\(A\)(機率 1)
從 \(A\) 移動:
- 右 → \(B\)(機率 \(1/4\))
- 下 → \(C\)(機率 \(1/4\))
- 左 → 出界 → 留在 \(A\)(機率 \(1/4\))
- 上 → 出界 → 留在 \(A\)(機率 \(1/4\))
所以:
\[
a_1 = \frac12, \quad b_1 = \frac14, \quad c_1 = \frac14, \quad d_1 = 0
\]
**(1)** \(b_1 = \frac14\) ✅
---
**2. 兩步轉移**
從 \(B\):
- 左 → \(A\)(\(1/4\))
- 右 → 出界 → 留在 \(B\)(\(1/4\))
- 下 → \(D\)(\(1/4\))
- 上 → 出界 → 留在 \(B\)(\(1/4\))
所以 \(B \to A: 1/4, \quad B \to B: 1/2, \quad B \to D: 1/4, \quad B \to C: 0\)
從 \(C\):
- 上 → \(A\)(\(1/4\))
- 下 → 出界 → 留在 \(C\)(\(1/4\))
- 右 → \(D\)(\(1/4\))
- 左 → 出界 → 留在 \(C\)(\(1/4\))
所以 \(C \to A: 1/4, \quad C \to C: 1/2, \quad C \to D: 1/4, \quad C \to B: 0\)
從 \(D\):
- 左 → \(C\)(\(1/4\))
- 右 → 出界 → 留在 \(D\)(\(1/4\))
- 上 → \(B\)(\(1/4\))
- 下 → 出界 → 留在 \(D\)(\(1/4\))
所以 \(D \to C: 1/4, \quad D \to D: 1/2, \quad D \to B: 1/4, \quad D \to A: 0\)
計算 \(n=2\):
\[
a_2 = a_1 \cdot \frac12 + b_1 \cdot \frac14 + c_1 \cdot \frac14 + d_1 \cdot 0
= \frac12 \cdot \frac12 + \frac14 \cdot \frac14 + \frac14 \cdot \frac14
= \frac14 + \frac1{16} + \frac1{16} = \frac38
\]
\[
b_2 = a_1 \cdot \frac14 + b_1 \cdot \frac12 + c_1 \cdot 0 + d_1 \cdot \frac14
= \frac12 \cdot \frac14 + \frac14 \cdot \frac12 + 0 + 0
= \frac18 + \frac18 = \frac14
\]
**(2)** \(b_2 = \frac18\) ❌
\[
c_2 = a_1 \cdot \frac14 + b_1 \cdot 0 + c_1 \cdot \frac12 + d_1 \cdot \frac14
= \frac12 \cdot \frac14 + 0 + \frac14 \cdot \frac12 + 0
= \frac18 + \frac18 = \frac14
\]
\[
d_2 = a_1 \cdot 0 + b_1 \cdot \frac14 + c_1 \cdot \frac14 + d_1 \cdot \frac12
= 0 + \frac1{16} + \frac1{16} + 0 = \frac18
\]
**(3)** \(a_2 + d_2 = \frac38 + \frac18 = \frac12\),不是 \(\frac34\) ❌
---
**3. 對稱性**
棋盤結構對稱:\(B\) 與 \(C\) 地位相同(初始在 \(A\) 時 \(b_n = c_n\) 對所有 \(n \ge 1\) 成立)。
**(4)** \(b_{99} = c_{99}\) ✅
---
**4. \(a_n + d_n\) 的性質**
計算 \(a_{n+1} + d_{n+1}\):
\[
a_{n+1} = \frac12 a_n + \frac14 b_n + \frac14 c_n
\]
\[
d_{n+1} = \frac14 b_n + \frac14 c_n + \frac12 d_n
\]
相加:
\[
a_{n+1} + d_{n+1} = \frac12 a_n + \frac12 b_n + \frac12 c_n + \frac12 d_n
\]
但 \(b_n + c_n = 1 - a_n - d_n\)(因為 \(b_n = c_n\) 且總和為 1),代入:
\[
a_{n+1} + d_{n+1} = \frac12 a_n + \frac12(1 - a_n - d_n) + \frac12 d_n
= \frac12 a_n + \frac12 - \frac12 a_n - \frac12 d_n + \frac12 d_n = \frac12
\]
所以 \(n \ge 1\) 時 \(a_n + d_n = \frac12\) 恆成立。
**(5)** \(a_{100} + d_{100} > \frac12\) ❌
---
**正確選項:** (1), (4)
\[
\boxed{1,4}
\] 報錯
ChatGPT DeepSeek
113學測數學B試題-13
矩陣方程與代數運算題”,”已知\( a,b,c,d \)為實數,且\(\begin{bmatrix} 1 & -1 \\ 3 & -2 \end{bmatrix}\begin{bmatrix} a \\ b \end{bmatrix} = \begin{bmatrix} 1 \\ 0 \end{bmatrix}\)。若\(\begin{bmatrix} 1 & -1 \\ 3 & -2 \end{bmatrix}\begin{bmatrix} 2a+1 \\ 2b+1 \end{bmatrix} = \begin{bmatrix} c \\ d \end{bmatrix}\),則\( c-3d \)的值為何?
[選填]首先解第一個矩陣方程:
由\(\begin{cases} a - b = 1 \\ 3a - 2b = 0 \end{cases}\),
由第一式得\( a = b + 1 \),代入第二式:
\( 3(b + 1) - 2b = 0 \implies b + 3 = 0 \implies b = -3 \),
則\( a = -3 + 1 = -2 \)。
接著計算第二個矩陣方程:
\( 2a + 1 = 2 \times (-2) + 1 = -3 \),
\( 2b + 1 = 2 \times (-3) + 1 = -5 \),
因此\(\begin{bmatrix} 1 & -1 \\ 3 & -2 \end{bmatrix}\begin{bmatrix} -3 \\ -5 \end{bmatrix} = \begin{bmatrix} -3 - (-5) \\ 3 \times (-3) - 2 \times (-5) \end{bmatrix} = \begin{bmatrix} 2 \\ 1 \end{bmatrix}\),
即\( c = 2 \),\( d = 1 \)。
故\( c - 3d = 2 - 3 \times 1 = -1 \)。 報錯
ChatGPT DeepSeek
04 – 113學測數學b試題14
某校全體高三學生都有報考學測數學\( A \)或數學\( B \),在這些學生中只報考數學\( A \)的學生占全體高三學生的\( \frac{3}{10} \)。報考數學\( A \)的學生中有\( \frac{5}{8} \)的學生同時也報考數學\( B \)。則只報考數學\( B \)的學生在該校所有報考數學\( B \)的學生中所占的比例為\( \frac{\boxed{}}{\boxed{}} \)。(化為最簡分數)
[選填]本題可透過**設定總人數**,結合集合比例關係求解:
1. **設定總人數並分析報考數學\( A \)的結構**:
設全校高三學生總人數為\( x \)。
- 只報考數學\( A \)的學生人數為\( \frac{3}{10}x \)。
- 設報考數學\( A \)的總人數為\( A \),其中只報考\( A \)的比例為\( 1 - \frac{5}{8} = \frac{3}{8} \),故\( \frac{3}{8}A = \frac{3}{10}x \implies A = \frac{4}{5}x \)。
2. **計算同時報考\( A \)和\( B \)、只報考\( B \)的人數**:
- 同時報考\( A \)和\( B \)的學生人數:\( \frac{5}{8}A = \frac{1}{2}x \)。
- 只報考\( B \)的學生人數:由總人數關係\( \frac{3}{10}x + B_{\text{只}} + \frac{1}{2}x = x \),得\( B_{\text{只}} = \frac{1}{5}x \)。
3. **計算比例**:
報考\( B \)的總人數為\( \frac{1}{5}x + \frac{1}{2}x = \frac{7}{10}x \),故只報考\( B \)的比例為\( \frac{\frac{1}{5}x}{\frac{7}{10}x} = \frac{2}{7} \)。
综上,答案為\(\boxed{\dfrac{2}{7}}\)。 報錯
ChatGPT DeepSeek
04 – 113學測數學b試題15
已知\( P_1、P_2、Q_1、Q_2、R \)為平面上相異五點,其中\( P_1、P_2、R \)三點不共線,且滿足\( \overrightarrow{P_1R} = 4\overrightarrow{P_1Q_1} \),\( \overrightarrow{P_2R} = 7\overrightarrow{P_2Q_2} \),則\( \overrightarrow{Q_1Q_2} = \frac{\boxed{15-1}}{\boxed{}} \overrightarrow{P_1Q_1} + \frac{\boxed{15-2}}{\boxed{15-3}} \overrightarrow{P_2Q_2} \)。
[選填]","首先,根據向量的分解與運算:
由\( \overrightarrow{P_1R} = 4\overrightarrow{P_1Q_1} \),得\( \overrightarrow{R} = \overrightarrow{P_1} + 4\overrightarrow{P_1Q_1} = \overrightarrow{P_1} + 4(\overrightarrow{Q_1} - \overrightarrow{P_1}) = -3\overrightarrow{P_1} + 4\overrightarrow{Q_1} \)。
由\( \overrightarrow{P_2R} = 7\overrightarrow{P_2Q_2} \),得\( \overrightarrow{R} = \overrightarrow{P_2} + 7\overrightarrow{P_2Q_2} = \overrightarrow{P_2} + 7(\overrightarrow{Q_2} - \overrightarrow{P_2}) = -6\overrightarrow{P_2} + 7\overrightarrow{Q_2} \)。
因此,\( -3\overrightarrow{P_1} + 4\overrightarrow{Q_1} = -6\overrightarrow{P_2} + 7\overrightarrow{Q_2} \),整理得:
\( 4\overrightarrow{Q_1} - 7\overrightarrow{Q_2} = 3\overrightarrow{P_1} - 6\overrightarrow{P_2} \),
\( 4\overrightarrow{Q_1} - 7\overrightarrow{Q_2} = 3(\overrightarrow{P_1} - 2\overrightarrow{P_2}) \)。
另,\( \overrightarrow{Q_1Q_2} = \overrightarrow{Q_2} - \overrightarrow{Q_1} \),嘗試用\( \overrightarrow{P_1Q_1} \)和\( \overrightarrow{P_2Q_2} \)表示:
由\( \overrightarrow{P_1Q_1} = \overrightarrow{Q_1} - \overrightarrow{P_1} \),得\( \overrightarrow{Q_1} = \overrightarrow{P_1} + \overrightarrow{P_1Q_1} \);
由\( \overrightarrow{P_2Q_2} = \overrightarrow{Q_2} - \overrightarrow{P_2} \),得\( \overrightarrow{Q_2} = \overrightarrow{P_2} + \overrightarrow{P_2Q_2} \)。
將\( \overrightarrow{Q_1}、\overrightarrow{Q_2} \)代入\( \overrightarrow{Q_1Q_2} = \overrightarrow{Q_2} - \overrightarrow{Q_1} \):
\( \overrightarrow{Q_1Q_2} = (\overrightarrow{P_2} + \overrightarrow{P_2Q_2}) - (\overrightarrow{P_1} + \overrightarrow{P_1Q_1}) = (\overrightarrow{P_2} - \overrightarrow{P_1}) + \overrightarrow{P_2Q_2} - \overrightarrow{P_1Q_1} \)。
再結合\( \overrightarrow{R} \)的兩種表示相等,即\( -3\overrightarrow{P_1} + 4\overrightarrow{Q_1} = -6\overrightarrow{P_2} + 7\overrightarrow{Q_2} \),代入\( \overrightarrow{Q_1}、\overrightarrow{Q_2} \)的表達式:
\( -3\overrightarrow{P_1} + 4(\overrightarrow{P_1} + \overrightarrow{P_1Q_1}) = -6\overrightarrow{P_2} + 7(\overrightarrow{P_2} + \overrightarrow{P_2Q_2}) \),
\( \overrightarrow{P_1} + 4\overrightarrow{P_1Q_1} = \overrightarrow{P_2} + 7\overrightarrow{P_2Q_2} \),
\( \overrightarrow{P_2} - \overrightarrow{P_1} = 4\overrightarrow{P_1Q_1} - 7\overrightarrow{P_2Q_2} \)。
將其代入\( \overrightarrow{Q_1Q_2} \)的表達式:
\( \overrightarrow{Q_1Q_2} = (4\overrightarrow{P_1Q_1} - 7\overrightarrow{P_2Q_2}) + \overrightarrow{P_2Q_2} - \overrightarrow{P_1Q_1} = 3\overrightarrow{P_1Q_1} - 6\overrightarrow{P_2Q_2} = \frac{3}{1}\overrightarrow{P_1Q_1} + \frac{-6}{1}\overrightarrow{P_2Q_2} \)。
因此,\( \overrightarrow{Q_1Q_2} = \frac{\boxed{3}}{\boxed{1}} \overrightarrow{P_1Q_1} + \frac{\boxed{-6}}{\boxed{1}} \overrightarrow{P_2Q_2} \)(若題中15-2、15-3為分子分母結構,也可整理為\( \overrightarrow{Q_1Q_2} = \frac{\boxed{3}}{\boxed{1}} \overrightarrow{P_1Q_1} + \frac{\boxed{-6}}{\boxed{1}} \overrightarrow{P_2Q_2} \),具體依題目格式調整)。 報錯
ChatGPT DeepSeek

