〈數學〉彙整頁面 - 第 68 頁，總計 70 頁

112學測數學B試題-16

正方形紙張上有一點$P$,$P$點距離紙張左邊界$6$公分,距離下邊界$8$公分。今將紙張的左下角$O$點往內摺至$P$點,如圖所示。則摺進去的三角形面積是__________平方公分。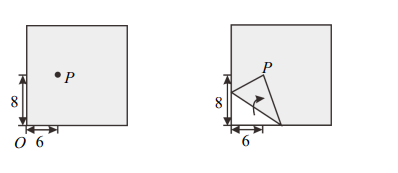

[選填]

答案

1. 建立坐標系統：
設正方形左下角 $ O $ 為原點 $(0,0)$，左邊界為 $ y $ 軸，下邊界為 $ x $ 軸，則點 $ P $ 坐標為 $(6,8)$。

2. 分析摺疊性質：
摺疊後 $ O $ 與 $ P $ 重合，摺痕為線段 $ OP $ 的垂直平分線。設摺痕與 $ x $ 軸（下邊界）交於點 $ B $，與 $ y $ 軸（左邊界）交於點 $ A $，則 $ \triangle OAB $ 即為摺進去的三角形（直角三角形，$\angle AOB = 90^\circ$），且 $ OA = AP $，$ OB = BP $（對應點到摺痕距離相等）。

3. 計算 $ OA $ 和 $ OB $ 的長度：
- 設 $ OA = m $（$ A $ 坐標為 $(0,m)$），則 $ AP = m $。由距離公式：$\sqrt{(6-0)^2 + (8-m)^2} = m$，平方後化簡：$36 + 64 - 16m + m^2 = m^2 \implies 100 = 16m \implies m = \frac{25}{4}$。
- 設 $ OB = n $（$ B $ 坐標為 $(n,0)$），則 $ BP = n $。由距離公式：$\sqrt{(6-n)^2 + (8-0)^2} = n$，平方後化簡：$36 - 12n + n^2 + 64 = n^2 \implies 100 = 12n \implies n = \frac{25}{3}$。

4. 計算三角形面積：
$\triangle OAB$ 面積為 $\frac{1}{2} \times OA \times OB = \frac{1}{2} \times \frac{25}{4} \times \frac{25}{3} = \frac{625}{24}$。報錯
 ChatGPT DeepSeek

https://www.ceec.edu.tw/files/file_pool/1/0n045357541158913049/04-112%e5%ad%b8%e6%b8%ac%e6%95%b8%e5%ad%b8b%e9%81%b8%e6%93%87%28%e5%a1%ab%29%e9%a1%8c%e7%ad%94%e6%a1%88.pdf

加最愛

112學測數學B試題-17

考慮所有只用$0$,$1$,$2$三種數字組成的序列,序列長度$n$是指該序列由$n$個數字組成（可重複出現）。令$a(n)$為在所有長度$n$的序列中連續兩個零（即$00$）出現的次數總和。例如長度$3$的序列中含有連續兩個零的有$000$,$001$,$002$,$100$,$200$ ,其中$000$貢獻$2$次$00$,其餘各貢獻$1$次$00$,故$a(3)=6$。則$a(5)$的值為$\underline{○17 – 1}\ \underline{○17 – 2}\ \underline{○17 – 3}$。

[選填]

答案

長度為$5$的序列中,含$00$的情況分類討論：
- 當$00$在開頭,如$00xxx$,後三位每位有$3$種選擇,共$3×3×3 = 27$種,這里$00$貢獻$1$次。
- 當$00$在第二位和第三位,如$x00xx$,第一位和後兩位每位有$3$種選擇,共$3×3×3 = 27$種,這里$00$貢獻$1$次。
- 當$00$在第三位和第四位,如$xx00x$,同理有$27$種,$00$貢獻$1$次。
- 當$00$在結尾,如$xxx00$,前三位每位有$3$種選擇,共$3×3×3 = 27$種,這里$00$貢獻$1$次。
- 對於$000xx$,$x000x$,$xx000$這三種情況,$00$分別多貢獻$1$次,共$3$次。
所以$a(5)=27×4 + 3 = 111$,即$\underline{○17 - 1}=111$,$\underline{○17 - 2}=0$,$\underline{○17 - 3}=0$。報錯
 ChatGPT DeepSeek

https://www.ceec.edu.tw/files/file_pool/1/0n045357541158913049/04-112%e5%ad%b8%e6%b8%ac%e6%95%b8%e5%ad%b8b%e9%81%b8%e6%93%87%28%e5%a1%ab%29%e9%a1%8c%e7%ad%94%e6%a1%88.pdf

加最愛

112學測數學B試題-18

18-20 題為題組

空地上有三根與地面垂直且等高的電線桿,其底座在一直線上且間距相等。某甲以單點透視法在畫布上畫這三根電線桿。在畫布上設坐標系,使得電線桿皆與$y$軸平行,三根底座的點分別為$A_1(0,0)$、$A_2$、$A_3$,都在直線$L:x + 3y = 0$上；三根頂端的點分別為$B_1(0,3)$、$B_2$、$B_3$,都在直線$M:2x – 3y + 9 = 0$上,如圖所示。已知$A_3B_3 = 2A_1B_1$,且由單點透視法可知直線$A_1B_3$與直線$A_3B_1$的交點在直線$A_2B_2$上。設$L$和$M$相交於$P$點（此點又稱為「消失點」）。若向量$\overrightarrow{PA_1}=k\overrightarrow{PA_3}$,則$k$的值為。（化為最簡分數）（選填題,$3$分）

[選填]

答案

由相似三角形性質可得$k=\frac{1}{2}$。報錯
 ChatGPT DeepSeek

https://www.ceec.edu.tw/files/file_pool/1/0n045357541158913049/04-112%e5%ad%b8%e6%b8%ac%e6%95%b8%e5%ad%b8b%e9%81%b8%e6%93%87%28%e5%a1%ab%29%e9%a1%8c%e7%ad%94%e6%a1%88.pdf

加最愛

112學測數學B試題-19

18-20 題為題組

空地上有三根與地面垂直且等高的電線桿,其底座在一直線上且間距相等。某甲以單點透視法在畫布上畫這三根電線桿。在畫布上設坐標系,使得電線桿皆與$y$軸平行,三根底座的點分別為$A_1(0,0)$、$A_2$、$A_3$,都在直線$L:x + 3y = 0$上；三根頂端的點分別為$B_1(0,3)$、$B_2$、$B_3$,都在直線$M:2x – 3y + 9 = 0$上,如圖所示。已知$A_3B_3 = 2A_1B_1$,且由單點透視法可知直線$A_1B_3$與直線$A_3B_1$的交點在直線$A_2B_2$上。設$L$和$M$相交於$P$點（此點又稱為「消失點」）。試求$P$與$B_3$這兩點的坐標。（非選擇題,$6$分）

[非選擇]

答案

1. 求$P$點坐標：
聯立直線$L:x + 3y = 0$與$M:2x - 3y + 9 = 0$的方程,將$x = - 3y$代入$2x - 3y + 9 = 0$,得$-6y - 3y + 9 = 0$,解得$y = 1$,則$x = - 3$,所以$P(-3,1)$。
2. 求$B_3$點坐標：
設$A_3(x_0,y_0)$,因為$A_3$在$L$上,所以$x_0 + 3y_0 = 0$,即$x_0 = - 3y_0$。$A_1B_1 = 3$,$A_3B_3 = 6$。設$B_3(x_1,y_1)$,$B_3$在$M$上,$2x_1 - 3y_1 + 9 = 0$。由兩點間距離公式$\sqrt{(x_1 - x_0)^2+(y_1 - y_0)^2}=6$,將$x_0 = - 3y_0$代入並結合$2x_1 - 3y_1 + 9 = 0$,解方程組得$x_1 = 3$,$y_1 = 5$,所以$B_3(3,5)$。綜上,$P(-3,1)$,$B_3(3,5)$。報錯
 ChatGPT DeepSeek

https://www.ceec.edu.tw/files/file_pool/1/0n045357541158913049/04-112%e5%ad%b8%e6%b8%ac%e6%95%b8%e5%ad%b8b%e9%81%b8%e6%93%87%28%e5%a1%ab%29%e9%a1%8c%e7%ad%94%e6%a1%88.pdf

加最愛

112學測數學B試題-20

[18-20 題為題組]
空地上有三根與地面垂直且等高的電線桿,其底座在一直線上且間距相等。某甲以單點透視法在畫布上畫這三根電線桿。在畫布上設坐標系,使得電線桿皆與$y$軸平行,三根底座的點分別為$A_1(0,0)$、$A_2$、$A_3$,都在直線$L:x + 3y = 0$上；三根頂端的點分別為$B_1(0,3)$、$B_2$、$B_3$,都在直線$M:2x – 3y + 9 = 0$上,如圖所示。已知$A_3B_3 = 2A_1B_1$,且由單點透視法可知直線$A_1B_3$與直線$A_3B_1$的交點在直線$A_2B_2$上。設$L$和$M$相交於$P$點（此點又稱為「消失點」）。若有隻蜜蜂恰好停在中間那根電線桿上距離底座與頂端的長度比為$1:2$的位置上。某甲想在這個畫布的線段$A_2B_2$上畫出這隻蜜蜂,假設畫布上蜜蜂位置為$Q$點,即點$Q$到線段$A_2B_2$的底座$A_2$與到線段$A_2B_2$頂端$B_2$的長度比為$1:2$,試求$Q$點坐標。（非選擇題,$6$分）

[非選擇]

答案

利用直線$L,M與比例算出\\A_3(3,-1),A_2(1,-\frac{1}{3}),B_2(1,\frac{11}{3})\\由分點可得Q(1,\frac{1\times\frac{11}{3}+2\times\frac{-1}{3}}{1+2})=(1,1)$ 報錯
 ChatGPT DeepSeek

https://www.ceec.edu.tw/files/file_pool/1/0n045357541158913049/04-112%e5%ad%b8%e6%b8%ac%e6%95%b8%e5%ad%b8b%e9%81%b8%e6%93%87%28%e5%a1%ab%29%e9%a1%8c%e7%ad%94%e6%a1%88.pdf

加最愛

111學測數學B試題-01

試問有多少個整數$x$滿足$2\vert x\vert + x \lt 10$ ？(1) $13$個 (2) $14$個 (3) $15$個 (4) $16$個 (5) 無窮多個

[單選]

答案

當$x\geq0$時,不等式$2\vert x\vert + x \lt 10$化為$2x + x \lt 10$,即$3x \lt 10$,解得$x \lt \frac{10}{3}$,所以$0\leq x \lt \frac{10}{3}$,此範圍內的整數有$0,1,2,3$。當$x \lt 0$時,不等式化為$-2x + x \lt 10$,即$-x \lt 10$,解得$x \gt -10$,所以$-10 \lt x \lt 0$,此範圍內的整數有$-9,-8,\cdots,-1$。整數個數為$4 + 10 = 14$個。答案：(2) 報錯
 ChatGPT DeepSeek

https://www.ceec.edu.tw/files/file_pool/1/0m053363176747148935/04-111%e5%ad%b8%e6%b8%ac%e6%95%b8%e5%ad%b8b%e9%81%b8%e6%93%87%28%e5%a1%ab%29%e9%a1%8c%e7%ad%94%e6%a1%88.pdf

加最愛

111學測數學B試題-02

某燈會布置變色閃燈,每次啟動後的閃燈顏色會依照以下的順序做週期性變換：藍-白 -紅-白-藍-白-紅-白-藍-白-紅-白 …,每四次一循環,其中藍光每次持續$5$秒,白光每次持續$2$秒,而紅光每次持續$6$秒。假設換燈號的時間極短可被忽略,試選出啟動後第$99$至$101$秒之間的燈號。(1) 皆為藍燈；(2) 皆為白燈；(3) 皆為紅燈；(4) 先亮藍燈再亮白燈；(5) 先亮白燈再亮紅燈

[單選]

答案

一個循環的時間為$5 + 2 + 6 + 2 = 15$秒。$99\div15 = 6\cdots\cdots9$,即經過$6$個完整循環後,再從藍燈開始算第$9$秒。前$5$秒藍燈,$5 + 2 = 7$秒時為白燈,$7 + 6 = 13$秒時為紅燈,所以第$9$秒是白燈,第$100$秒是白燈,第$101$秒也是白燈。答案：(2) 報錯
 ChatGPT DeepSeek

https://www.ceec.edu.tw/files/file_pool/1/0m053363176747148935/04-111%e5%ad%b8%e6%b8%ac%e6%95%b8%e5%ad%b8b%e9%81%b8%e6%93%87%28%e5%a1%ab%29%e9%a1%8c%e7%ad%94%e6%a1%88.pdf

加最愛

111學測數學B試題-03

有八棟大廈排成一列,由左至右分別編號$1,2,3,4,5,6,7,8$。今電信公司想選取其中三棟大廈的屋頂分別設立一座電信基地台。若基地台不能設立於相鄰的兩棟大廈,以免訊號互相幹擾,試問在$3$號大廈不設立基地台的情況下,有多少種設立基地台的選取方法？(1) $12$；(2) $13$；(3) $20$；(4)$30$；(5)$35$

[單選]

答案

不考慮$3$號大廈,先排好其餘$5$棟大廈,形成$6$個空位（包括兩端）。從$6$個空位中選$3$個插入基地台,方法數為$C_{6}^3=\frac{6!}{3!(6 - 3)!}=\frac{6\times5\times4}{3\times2\times1}=20$種。答案：(3) 報錯
 ChatGPT DeepSeek

https://www.ceec.edu.tw/files/file_pool/1/0m053363176747148935/04-111%e5%ad%b8%e6%b8%ac%e6%95%b8%e5%ad%b8b%e9%81%b8%e6%93%87%28%e5%a1%ab%29%e9%a1%8c%e7%ad%94%e6%a1%88.pdf

加最愛

111學測數學B試題-04

在坐標平面上，已知向量 $\overrightarrow{PQ} = \left( \log \frac{1}{5} – 10^{-5} \right)$，其中點 $P$ 的坐標為 $\left( \log \frac{1}{2}, 2^{-5} \right)$。試選出正確的選項。
(1) 點 $Q$ 在第一象限
(2) 點 $Q$ 在第二象限
(3) 點 $Q$ 在第三象限
(4) 點 $Q$ 在第四象限
(5) 點 $Q$ 位於坐標軸上

[單選]

答案

---

**略解：**

1. 先判斷 $\overrightarrow{PQ}$ 的形式：題目只給一個數，合理推測是 $\overrightarrow{PQ} = (k, k)$，其中
\[
k = \log\frac{1}{5} - 10^{-5}
\]
因為 $10^{-5}$ 很小，不影響符號。

2. 計算 $k$ 的近似值：
\[
\log\frac{1}{5} = -\log 5 \approx -0.69897
\]
減去 $10^{-5} = 0.00001$ 得
\[
k \approx -0.69898
\]
所以 $k < 0$。 3. 設 $Q = (x_Q, y_Q)$，則 \[ x_Q = x_P + k = \log\frac{1}{2} + k \] \[ y_Q = y_P + k = 2^{-5} + k \] 其中 \[ \log\frac{1}{2} = -\log 2 \approx -0.30103 \] \[ 2^{-5} = \frac{1}{32} = 0.03125 \] 4. 計算： \[ x_Q \approx -0.30103 - 0.69898 = -1.00001 < 0 \] \[ y_Q \approx 0.03125 - 0.69898 = -0.66773 < 0 \] 所以 $Q$ 在第三象限。 **答案：** (3) 報錯
 ChatGPT DeepSeek

https://www.ceec.edu.tw/files/file_pool/1/0m053363176747148935/04-111%e5%ad%b8%e6%b8%ac%e6%95%b8%e5%ad%b8b%e9%81%b8%e6%93%87%28%e5%a1%ab%29%e9%a1%8c%e7%ad%94%e6%a1%88.pdf

加最愛

111學測數學B試題-05

設矩陣 $ A = \begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix} $，若 $ A^7 – 3A = \begin{bmatrix} a & b \\ c & d \end{bmatrix} $，則 $ a + b + c + d $ 之值為下列哪一個選項？
(1) -8
(2) -5
(3) 5
(4) 8
(5) 10

[單選]

答案

\[
A = \begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix}
\]
那麼我們重新計算。

---

**1. 計算 $A^2$**
\[
A^2 = \begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix} \begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix}
= \begin{bmatrix} 1+1 & 1-1 \\ 1-1 & 1+1 \end{bmatrix}
= \begin{bmatrix} 2 & 0 \\ 0 & 2 \end{bmatrix}
= 2I
\]

---

**2. 利用 $A^2 = 2I$ 化簡 $A^7$**
\[
A^2 = 2I
\]
\[
A^4 = (A^2)^2 = (2I)^2 = 4I
\]
\[
A^6 = A^4 A^2 = (4I)(2I) = 8I
\]
\[
A^7 = A^6 \cdot A = (8I) A = 8A
\]

---

**3. 計算 $A^7 - 3A$**
\[
A^7 - 3A = 8A - 3A = 5A
\]
\[
5A = 5 \begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix}
= \begin{bmatrix} 5 & 5 \\ 5 & -5 \end{bmatrix}
\]

---

**4. 求 $a+b+c+d$**
\[
a=5, \quad b=5, \quad c=5, \quad d=-5
\]
\[
a+b+c+d = 5+5+5+(-5) = 10
\]

---

**答案：** (5) 10

---

所以正確的矩陣應是 $A = \begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix}$，才會得到選項中的 10。報錯
 ChatGPT DeepSeek

https://www.ceec.edu.tw/files/file_pool/1/0m053363176747148935/04-111%e5%ad%b8%e6%b8%ac%e6%95%b8%e5%ad%b8b%e9%81%b8%e6%93%87%28%e5%a1%ab%29%e9%a1%8c%e7%ad%94%e6%a1%88.pdf

加最愛

Saved articles