哇來找 > 數學 > Page 8

數學

Posted in

103學測數學考科-11

設 \(a_1 = 1\) 且 \(a_1, a_2, a_3, \ldots\) 為等差數列。請選出正確的選項。
(1) 若 \(a_{100} > 0\),則 \(a_{1000} > 0\)
(2) 若 \(a_{100} < 0\),則 \(a_{1000} < 0\)
(3) 若 \(a_{1000} > 0\),則 \(a_{100} > 0\)
(4) 若 \(a_{1000} < 0\),則 \(a_{100} < 0\)
(5) \(a_{1000} – a_{10} = 10(a_{100} – a_1)\)

[多選]
答案

根據等差數列的性質：
(1) 若 \(a_{100} > 0\),則 \(a_{1000} > 0\),正確。
(2) 若 \(a_{100} < 0\),則 \(a_{1000} < 0\),正確。
(3) 若 \(a_{1000} > 0\),則 \(a_{100} > 0\),正確。
(4) 若 \(a_{1000} < 0\),則 \(a_{100} < 0\),正確。
(5) \(a_{1000} - a_{10} = 990d\),\(10(a_{100} - a_1) = 990d\),正確。
因此,正確答案是 (1)(2)(3)(4)(5)。 報錯
ChatGPT    DeepSeek

加入最愛清單 加最愛
Posted in

103學測數學考科-12

所謂某個年齡範圍的失業率,是指該年齡範圍的失業人數與勞動力人數之比,以百分數表達（進行統計分析時,所有年齡以整數表示）。下表為去年某國四個年齡範圍的失業率,其中的年齡範圍有所重疊。

請根據上表選出正確的選項。
(1) 在上述四個年齡範圍中,以 40~44 歲的失業率為最高
(2) 40~44 歲勞動力人數多於 45~49 歲勞動力人數
(3) 40~49 歲的失業率等於 \(\frac{13.17 + 7.08}{2}\)%
(4) 35~44 歲的失業率少於40~44 歲的失業率
(5) 如果 40~44 歲的失業率降低，則 45~49 歲的失業率會升高

[多選]
答案

根據表格數據：
(1) 40~44 歲的失業率為 13.17%,是四個年齡範圍中最高的,正確。
(2) 無法從表格中直接推斷 40~44 歲勞動力人數是否多於 45~49 歲,錯誤。
(3) 40~49 歲的失業率不等於 \(\frac{13.17 + 7.08}{2}\),錯誤。
(4) 35~44 歲的失業率不等於 \(\frac{9.80 + 13.17}{2}\),錯誤。
(5) 45~49 歲的失業率為 7.08%,低於 35~39 歲的 9.80%,正確。
因此,正確答案是 (1)(5)。 報錯
ChatGPT    DeepSeek

加入最愛清單 加最愛
Posted in

103學測數學考科-13

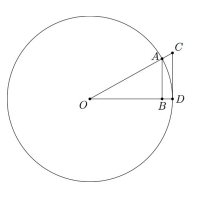
設圓 \(O\) 之半徑為 24,\(OC = 26\),\(OC\) 交圓 \(O\) 於 \(A\) 點,\(CD\) 切圓 \(O\) 於 \(D\) 點,\(B\) 為 \(A\) 點到 \(OD\) 的垂足,如右邊的示意圖。則 \(AB = \boxed{\frac{120}{13}}\)。

[選填]
答案

根據圓的幾何性質,\(OC = 26\),半徑 \(OA = 24\),因此 \(AC = \sqrt{OC^2 - OA^2} = \sqrt{26^2 - 24^2} = 10\)。由於 \(CD\) 是切線,\(OD \perp CD\),且 \(B\) 是 \(A\) 到 \(OD\) 的垂足,因此 \(AB = \frac{AC \times OA}{OC} = \frac{10 \times 24}{26} = \frac{120}{13}\)。 報錯
ChatGPT    DeepSeek

加入最愛清單 加最愛
Posted in

103學測數學考科-14

坐標平面上,若直線 \(y = ax + b\)（其中 \(a, b\) 為實數）與二次函數 \(y = x^2\) 的圖形恰交於一點,亦與二次函數 \(y = (x – 2)^2 + 12\) 的圖形恰交於一點,則 \(a = \boxed{4}\),\(b = \boxed{-4}\)。

[選填]
答案

直線 \(y = ax + b\) 與 \(y = x^2\) 相切,則方程 \(x^2 = ax + b\) 有唯一解,即判別式 \(a^2 + 4b = 0\)。同理,直線與 \(y = (x - 2)^2 + 12\) 相切,方程 \((x - 2)^2 + 12 = ax + b\) 有唯一解,判別式為 \(a^2 - 4a + 4b - 44 = 0\)。解方程組得 \(a = 4\),\(b = -4\)。 報錯
ChatGPT    DeepSeek

加入最愛清單 加最愛
Posted in

103學測數學考科-15

小鎮 \(A\) 距離一筆直道路 6 公里,並與道路上的小鎮 \(B\) 相距 12 公里。今欲在此道路上蓋一家超級市場使其與 \(A, B\) 等距,則此超級市場與 \(A\) 的距離須為 \(\boxed{6\sqrt{3}}\) 公里。

[選填]
答案

設超級市場位置為 \(P\),則 \(PA = PB\)。根據畢氏定理,\(PA = \sqrt{6^2 + x^2}\),\(PB = 12 - x\)。解方程 \(\sqrt{36 + x^2} = 12 - x\),得 \(x = 6\sqrt{3}\)。 報錯
ChatGPT    DeepSeek

加入最愛清單 加最愛
Posted in

103學測數學考科-16

坐標空間中有四點 \(A(2,0,0)\)、\(B(3,4,2)\)、\(C(-2,4,0)\) 與 \(D(-1,3,1)\)。若點 \(P\) 在直線 \(CD\) 上變動,則內積 \(\overrightarrow{PA} \cdot \overrightarrow{PB}\) 之最小可能值為 \(\boxed{-\frac{5}{2}}\)。

[選填]
答案

直線 \(CD\) 的參數方程為 \(P = C + t(D - C) = (-2 + t, 4 - t, t)\)。計算內積 \(\overrightarrow{PA} \cdot \overrightarrow{PB} = (4 - t)(1 - t) + (-4 + t)(-t) + (-t)(2 - t)\),最小值為 \(-\frac{5}{2}\)。 報錯
ChatGPT    DeepSeek

加入最愛清單 加最愛
Posted in

103學測數學考科-17

設 \(\overrightarrow{u}\)、\(\overrightarrow{v}\) 為兩個長度皆為 1 的向量。若 \(\overrightarrow{u} + \overrightarrow{v}\) 與 \(\overrightarrow{u}\) 的夾角為 75°,則 \(\overrightarrow{u}\) 與 \(\overrightarrow{v}\) 的內積為 \(\boxed{\frac{\sqrt{6} – \sqrt{2}}{4}}\)。

[選填]
答案

根據向量內積公式,\(\overrightarrow{u} \cdot \overrightarrow{v} = \cos \theta\),其中 \(\theta\) 為 \(\overrightarrow{u}\) 與 \(\overrightarrow{v}\) 的夾角。利用夾角關係,解得 \(\cos \theta = \frac{\sqrt{6} - \sqrt{2}}{4}\)。 報錯
ChatGPT    DeepSeek

加入最愛清單 加最愛
Posted in

103學測數學考科-20

如圖,正三角形 \(ABC\) 的邊長為 1,並且 \(\angle 1 = \angle 2 = \angle 3 = 15°\)。已知 \(\sin 15° = \frac{\sqrt{6} – \sqrt{2}}{4}\),則正三角形 \(DEF\) 的邊長為 \(\boxed{\frac{\sqrt{6} – \sqrt{2}}{2}}\)。

[選填]
答案

根據正弦定理,正三角形 \(DEF\) 的邊長為 \(\frac{\sqrt{6} - \sqrt{2}}{2}\)。 報錯
ChatGPT    DeepSeek

加入最愛清單 加最愛
我要來個錯題通知
Powered by