104以前學測數學
104學測數學考科-12
104學測數學考科-13
小燦預定在陽台上種植玫瑰、百合、菊花和向日葵等四種盆栽。如果陽台上的空間最多能種 8 盆,可以不必擺滿,並且每種花至少一盆,則小燦買盆栽的方法共有 \(\boxed{~~~~~~~~~~}\) 種。
### 步驟1:轉化問題
設玫瑰、百合、菊花、向日葵分別種 \( x, y, z, w \) 盆,滿足 \( x + y + z + w \leq 8 \),且 \( x, y, z, w \geq 1 \)。
令 \( x' = x - 1 \),\( y' = y - 1 \),\( z' = z - 1 \),\( w' = w - 1 \)(則 \( x', y', z', w' \geq 0 \)),問題轉化為求 \( x' + y' + z' + w' \leq 4 \)(因為 \( 8 - 4 = 4 \))的非負整數解的個數。
### 步驟2:分情況討論(按剩餘盆數 \( k = x' + y' + z' + w' \),\( k = 0,1,2,3,4 \))
- 當 \( k = 0 \) 時:只有 \( 1 \) 種方法(四盆花各一盆)。
- 當 \( k = 1 \) 時:從4種花中選1種多植1盆,有 \( \binom{4}{1} = 4 \) 種方法。
- 當 \( k = 2 \) 時:
- 選1種花多植2盆:\( \binom{4}{1} = 4 \) 種;
- 選2種花各多植1盆:\( \binom{4}{2} = 6 \) 種;
共 \( 4 + 6 = 10 \) 種。
- 當 \( k = 3 \) 時:
- 選1種花多植3盆:\( \binom{4}{1} = 4 \) 種;
- 選1種花多植2盆、另1種花多植1盆:\( \binom{4}{1} \times \binom{3}{1} = 12 \) 種;
共 \( 4 + 12 = 16 \) 種。
- 當 \( k = 4 \) 時:
- 選1種花多植4盆:\( \binom{4}{1} = 4 \) 種;
- 選1種花多植3盆、另1種花多植1盆:\( \binom{4}{1} \times \binom{3}{1} = 12 \) 種;
- 選2種花各多植2盆:\( \binom{4}{2} = 6 \) 種;
- 選1種花多植2盆、另2種花各多植1盆:\( \binom{4}{1} \times \binom{3}{2} = 12 \) 種;
共 \( 4 + 12 + 6 + 12 = 34 \) 種。
### 步驟3:求和
將所有情況相加:\( 1 + 4 + 10 + 16 + 34 = 65 \) 種。
104學測數學考科-14
D. 平面 \( x – y + z = 0 \) 與平面 \( x = 2 \)、\( x – y = -2 \)、\( x + y = 2 \) 分別相交所得的三直線可圍成一個三角形。此三角形之周長化為最簡根式,可表為 \( a\sqrt{b} + c\sqrt{d} \),其中 \( a, b, c, d \) 為正整數且 \( b \lt d \),則 \( a = \boxed{17} \),\( b = \boxed{18} \),\( c = \boxed{19} \),\( d = \boxed{20} \)。
### 略解
要解決此問題,需先求三平面兩兩相交的直線方程,再求三角形的三個頂點,最後計算各邊長並求和得到周長。
#### 步驟1:求三條交線的方程
- **平面 \( x - y + z = 0 \) 與 \( x = 2 \) 的交線**:
將 \( x = 2 \) 代入 \( x - y + z = 0 \),得 \( 2 - y + z = 0 \implies z = y - 2 \)。
交線方程為 \( \begin{cases} x = 2 \\ z = y - 2 \end{cases} \)(參數化:\( x = 2, y = t, z = t - 2 \),\( t \) 為參數)。
- **平面 \( x - y + z = 0 \) 與 \( x - y = -2 \) 的交線**:
由 \( x - y = -2 \implies y = x + 2 \),代入 \( x - y + z = 0 \),得 \( x - (x + 2) + z = 0 \implies z = 2 \)。
交線方程為 \( \begin{cases} y = x + 2 \\ z = 2 \end{cases} \)(參數化:\( x = t, y = t + 2, z = 2 \),\( t \) 為參數)。
- **平面 \( x - y + z = 0 \) 與 \( x + y = 2 \) 的交線**:
由 \( x + y = 2 \implies y = 2 - x \),代入 \( x - y + z = 0 \),得 \( x - (2 - x) + z = 0 \implies z = 2 - 2x \)。
交線方程為 \( \begin{cases} y = 2 - x \\ z = 2 - 2x \end{cases} \)(參數化:\( x = t, y = 2 - t, z = 2 - 2t \),\( t \) 為參數)。
#### 步驟2:求三角形的三個頂點
- **頂點 \( A \)**:交線 \( x = 2 \) 與 \( y = x + 2 \) 的交點。
代入 \( x = 2 \) 到 \( y = x + 2 \),得 \( y = 4 \),再代入 \( z = 2 \),故 \( A(2, 4, 2) \)。
- **頂點 \( B \)**:交線 \( y = x + 2 \) 與 \( y = 2 - x \) 的交點。
聯立 \( y = x + 2 \) 和 \( y = 2 - x \),得 \( x + 2 = 2 - x \implies x = 0 \),則 \( y = 2 \),\( z = 2 \),故 \( B(0, 2, 2) \)。
- **頂點 \( C \)**:交線 \( y = 2 - x \) 與 \( x = 2 \) 的交點。
代入 \( x = 2 \) 到 \( y = 2 - x \),得 \( y = 0 \),再代入 \( z = y - 2 \),得 \( z = -2 \),故 \( C(2, 0, -2) \)。
#### 步驟3:計算各邊的長度
- **邊長 \( AB \)**:
由距離公式 \( \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2} \),得
\[
AB = \sqrt{(2 - 0)^2 + (4 - 2)^2 + (2 - 2)^2} = \sqrt{4 + 4 + 0} = \sqrt{8} = 2\sqrt{2}
\]
- **邊長 \( BC \)**:
\[
BC = \sqrt{(0 - 2)^2 + (2 - 0)^2 + (2 - (-2))^2} = \sqrt{4 + 4 + 16} = \sqrt{24} = 2\sqrt{6}
\]
- **邊長 \( CA \)**:
\[
CA = \sqrt{(2 - 2)^2 + (0 - 4)^2 + (-2 - 2)^2} = \sqrt{0 + 16 + 16} = \sqrt{32} = 4\sqrt{2}
\]
#### 步驟4:計算周長
周長 \( = AB + BC + CA = 2\sqrt{2} + 2\sqrt{6} + 4\sqrt{2} = 6\sqrt{2} + 2\sqrt{6} \)。
對比形式 \( a\sqrt{b} + c\sqrt{d} \)(其中 \( b < d \)),可得 \( a = 6 \),\( b = 2 \),\( c = 2 \),\( d = 6 \)。
综上,\( a = \boxed{6} \),\( b = \boxed{2} \),\( c = \boxed{2} \),\( d = \boxed{6} \)。 報錯
ChatGPT DeepSeek
104學測數學考科-15
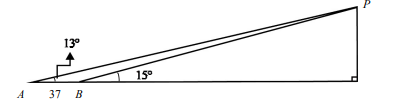
坐標平面上,直線 \( L_1 \) 與 \( L_2 \) 的方程式分別為 \( x + 2y = 0 \) 與 \( 3x – 5y = 0 \)。為了確定平面上某一定點 \( P \) 的坐標,從 \( L_1 \) 上的一點 \( Q_1 \) 偵測得向量 \( \overrightarrow{Q_1P} = (-7, 9) \),再從 \( L_2 \) 上的點 \( Q_2 \) 偵測得向量 \( \overrightarrow{Q_2P} = (-6, -8) \),則 \( P \) 點的坐標為(____ , ____)。
### 略解
要解決此問題,可透過**設點座標、利用直線方程與向量關係**建立方程組求解,步驟如下:
1. **設點座標**
設 \( P(x, y) \),\( Q_1(a, b) \)(在 \( L_1 \) 上),\( Q_2(c, d) \)(在 \( L_2 \) 上)。
- 因 \( Q_1 \) 在 \( L_1: x + 2y = 0 \) 上,故 \( a + 2b = 0 \);
- 因 \( Q_2 \) 在 \( L_2: 3x - 5y = 0 \) 上,故 \( 3c - 5d = 0 \)。
2. **由向量關係列方程**
- 由 \( \overrightarrow{Q_1P} = (-7, 9) \),得 \( \begin{cases} x - a = -7 \\ y - b = 9 \end{cases} \implies \begin{cases} a = x + 7 \\ b = y - 9 \end{cases} \);
- 由 \( \overrightarrow{Q_2P} = (-6, -8) \),得 \( \begin{cases} x - c = -6 \\ y - d = -8 \end{cases} \implies \begin{cases} c = x + 6 \\ d = y + 8 \end{cases} \)。
3. **代入直線方程解聯立**
- 將 \( a = x + 7 \)、\( b = y - 9 \) 代入 \( a + 2b = 0 \),得:
\[
(x + 7) + 2(y - 9) = 0 \implies x + 2y = 11 \tag{1}
\]
- 將 \( c = x + 6 \)、\( d = y + 8 \) 代入 \( 3c - 5d = 0 \),得:
\[
3(x + 6) - 5(y + 8) = 0 \implies 3x - 5y = 22 \tag{2}
\]
- 聯立 \( (1)(2) \),由 \( (1) \) 得 \( x = 11 - 2y \),代入 \( (2) \):
\[
3(11 - 2y) - 5y = 22 \implies 33 - 6y - 5y = 22 \implies 11y = 11 \implies y = 1
\]
再代入 \( x = 11 - 2y \),得 \( x = 11 - 2 \times 1 = 9 \)。
104學測數學考科-16
小華準備向銀行貸款3百萬元當做創業基金,其年利率為3%,約定三年期滿一次還清貸款的本利和。銀行貸款一般以複利(每年複利一次)計息還款,但給小華創業優惠改以單利計息還款。試問在此優惠下,小華在三年期滿還款時可以比一般複利計息少繳 ㉓㉔㉕㉖ 元。
104學測數學考科-17
某 一 公司,有 A、 B、 C 三個 營業據點,開始時 各有 36 位營業員, 為了讓營 業員了解各 據點業務 狀況,所 以進行兩 次調動。 每次調動 都是:將當時 A 據點營業 員中的 1/6 調到 B 據點、 1/6 調到 C 據點;將當時 B 據點營業 員中的 1/6 調到 A 據點、 1/3 調到 C 據點;將當時 C 據點營業 員中的 1/6 調到 A 據點、 1/6 調到 B 據點。則兩次的 調動後, C 據點有 ㉗㉘ 位 營業員。
第一次調動:A據點剩 \(36×(1 - \frac{1}{6}-\frac{1}{6}) = 24\) 位;B據點有 \(36×\frac{1}{6}+36×(1 - \frac{1}{6}-\frac{1}{3}) = 24\) 位;C據點有 \(36×\frac{1}{6}+36×\frac{1}{6}+36×(1 - \frac{1}{6}-\frac{1}{6}) = 36\) 位。第二次調動:A據點有 \(24×(1 - \frac{1}{6}-\frac{1}{6}) + 24×\frac{1}{6}+36×\frac{1}{6}=24\) 位;B據點有 \(24×\frac{1}{6}+24×(1 - \frac{1}{6}-\frac{1}{3})+36×\frac{1}{6}=24\) 位;C據點有 \(24×\frac{1}{6}+24×\frac{1}{6}+36×(1 - \frac{1}{6}-\frac{1}{6}) = 32\) 位。所以答案是32位。 報錯
ChatGPT DeepSeek
104學測數學考科-18
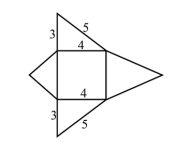
有一底面為正方形的四角錐,其展開圖如下圖所示,其中兩側面的三角形邊長為3,4,5 ,則此角錐的體積為 __________。(化為最簡根式)
104學測數學考科-19
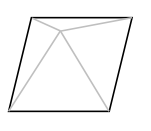
在空間中,一個斜面的「坡度」定義為斜面與水平面夾角 \(\theta\) 的正切值 \(\tan\theta\) 。若一金字塔(底部為一正方形,四個斜面為等腰三角形)的每一個斜面的坡度皆為 \(\frac{2}{5}\) ,如圖。則相鄰斜面的夾角的餘弦函數的絕對值為 ________。(化為最簡分數)
104學測數學考科-20
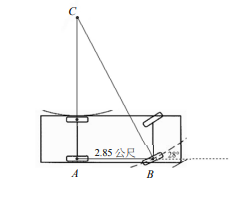
下圖為汽車迴轉示意圖。汽車迴轉時,將方向盤轉動到極限,以低速讓汽車進行轉向圓周運動,汽車轉向時所形成的圓周的半徑就是迴轉半徑,如圖中的BC即是。已知在低速前進時,圖中A處的輪胎行進方向與AC垂直,B處的輪胎行進方向與BC垂直。在圖中,已知軸距AB為2.85公尺,方向盤轉到極限時,輪子方向偏了28度 ,試問此車的迴轉半徑BC為 ㊱.㊲ 公尺。(小數點後第 一位以下四捨五入, \(\sin28^{\circ}\approx0.4695\) , \(\cos28^{\circ}\approx0.8829\) )