〈106學測數學〉彙整頁面

106學測數學考科–01

已知某校老師玩過「寶可夢」的比率為 $ r_1 $，而學生玩過的比率為 $ r_2 $，其中 $ r_1 \neq r_2 $。由下列選項中的資訊，請選出可以判定全校師生玩過「寶可夢」的比率之選項：
(1)全校老師與學生比率
(2)全校老師人數
(3)全校學生人數
(4)全校師生人數
(5)全校師生玩過「寶可夢」人數。

答案

設全校老師人數 $ n_1 $、學生人數 $ n_2 $。全校玩過「寶可夢」的比率為 $ \frac{n_1 r_1 + n_2 r_2}{n_1+n_2} $，其中 $ \frac{n_1}{n_1+n_2} $、$ \frac{n_2}{n_1+n_2} $ 分別為全校老師與學生的比率。故選(1)。答案：(1) 報錯
 ChatGPT DeepSeek

加最愛

106學測數學考科–02

某個手機程式，每次點擊螢幕上的數$a$後，螢幕上的數會變成 $ a^2 $。當一開始時螢幕上的數b為正且連續點擊螢幕三次後，螢幕上的數接近 $ 81^3 $，試問實數$b$最接近下列哪一個選項？
(1)$1.7$ (2)$3$ (3)$5.2$ (4)$9$ (5)$81$。

答案

依題意，得 $ (((b^2)^2)^2) = b^8 \approx 8!^2 \Rightarrow b^8 \approx (40320)^2 \Rightarrow b \approx 40320^{1/4} \approx 5.2 $。故選(3)。答案：(3) 報錯
 ChatGPT DeepSeek

加最愛

設 $\Gamma : \frac{y^2}{a^2} -\frac{x^2}{b^2}=1$ 為坐標平面上一雙曲線，且其通過第一象限的漸近線為 $\ell$。考慮動點 $(t, t^2)$，從時間 $ t = 0 $ 時出發。當 $ t > 0 $ 時，請選出正確的選項：
(1)此動點不會碰到 $\Gamma$，也不會碰到 $\ell$
(2)此動點會碰到 $\Gamma$，但不會碰到 $\ell$
(3)此動點會碰到 $\ell$，但不會碰到 $\Gamma$
(4)此動點會先碰到 $\Gamma$，再碰到 $\ell$
(5)此動點會先碰到 $\ell$，再碰到 $\Gamma$。

答案

動點 $(t, t^2)$ 在拋物線 $y=x^2$ 上。當 $x>0$ 且 $x$ 接近 0 時，$x^2 \lt \frac{a}{b}x$，故動點會先碰到漸近線 $\ell$，再碰到雙曲線 $\Gamma$。故選(5)。答案：(5) 報錯
 ChatGPT DeepSeek

加最愛

106學測數學考科–04

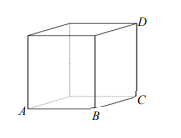
在右下圖的正立方體上有兩質點分別自頂點 $A, C$ 同時出發，各自以等速直線運動分別向頂點 $B, D$ 前進，且在 1 秒後分別同時到達 $B, D$。請選出這段時間兩質點距離關係的正確選項。

(1) 兩質點的距離固定不變
(2) 兩質點的距離越來越小
(3) 兩質點的距離越來越大
(4) 在 $\frac{1}{2}$ 秒時兩質點的距離最小
(5) 在 $\frac{1}{2}$ 秒時兩質點的距離最大。

答案

設 $t$ 秒時，質點位置 $P(1, t, 0)$、$Q(0, 1, t)$。距離 $PQ = \sqrt{1 + (t-1)^2 + t^2} = \sqrt{2t^2 - 2t + 2} = \sqrt{2(t - \frac{1}{2})^2 + \frac{3}{2}}$。當 $t=\frac{1}{2}$ 時有最小值。故選(4)。答案：(4) 報錯
 ChatGPT DeepSeek

加最愛

106學測數學考科–05

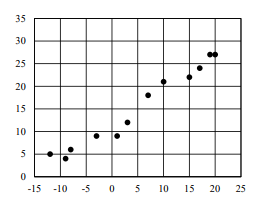
下圖是某城市在2016年的各月最低溫（橫軸x）與最高溫（縱軸y）的散布圖。

今以溫差（最高溫減最低溫）為橫軸且最高溫為縱軸重新繪製一散布圖，試依此選出正確的選項：
(1)最高溫與溫差為正相關，且它們的相關性比最高溫與最低溫的相關性強
(2)最高溫與溫差為正相關，且它們的相關性比最高溫與最低溫的相關性弱
(3)最高溫與溫差為負相關，且它們的相關性比最高溫與最低溫的相關性強
(4)最高溫與溫差為負相關，且它們的相關性比最高溫與最低溫的相關性弱
(5)最高溫與溫差為零相關。

答案

溫差越大，最高溫有越低趨勢，故為負相關。新散布圖比原圖（最高溫與最低溫）較不接近一直線，相關性較弱。故選(4)。答案：(4) 報錯
 ChatGPT DeepSeek

加最愛

106學測數學考科–06

試問有多少個實數 $ x $ 滿足 $\frac{\pi}{2} \leq x \leq \frac{3\pi}{2}$ 且 $\cos x^0 \leq \cos x$？
(1) 0 個 (2) 1 個 (3) 2 個 (4) 4 個 (5) 無窮多個。

答案

$x^0$ 約介於 1.57° 與 4.71° 之間，$\cos x^0 > 0$。而 $x$ 弧度在 $\frac{\pi}{2}$ 到 $\frac{3\pi}{2}$ 之間，$\cos x \leq 0$。故 $\cos x^0 > \cos x$，恆成立，無解。故選(1)。答案：(1) 報錯
 ChatGPT DeepSeek

加最愛

106學測數學考科–07

小明想要安排從星期一到星期五共五天的午餐計畫。他的餐點共有四種選擇：牛肉麵、大油麵、咖喱飯及排骨飯。小明想要依據下列兩原則來安排他的午餐：
(甲)每天只選一種餐點但這五天中每一種餐點至少各點一次
(乙)連續兩天的餐點不能重複且不連續兩天吃麵食
根據上述原則，小明這五天共有幾種不同的午餐計畫？
(1) 52 (2) 60 (3) 68 (4) 76 (5) 84。

答案

令R表飯，N表麵。分類討論：三N：NRNRN→12種；二N：ORNRNR→12種；RRNRN、RNRRN、NRNRN、NRNRR→32種；RRNRN→4種。總計12+12+32+4=60種。故選(2)。答案：(2) 報錯
 ChatGPT DeepSeek

加最愛

106學測數學考科–08

設m, n為小於或等於4的相異正整數且a, b為非零實數。已知函數$f(x) = ax^m$與函數$g(x) = bx^n$的圖形恰有3個相異交點，請選出可能的選項。
(1) m, n皆為偶數且a, b同號
(2) m, n皆為偶數且a, b異號
(3) m, n皆為奇數且a, b同號
(4) m, n皆為奇數且a, b異號
(5) m, n為一奇一偶。

答案

解 $ax^m = bx^n \Rightarrow x^n (ax^{m-n} - b) = 0$。需恰有3個相異實根。
(1) m, n偶，a, b同號：$x=0$（重根），$x=\pm \sqrt[m-n]{\frac{b}{a}}$，共3個相異實根。
(2) m, n偶，a, b異號：$x=0$，另兩根為虛數，僅1實根。
(3) m, n奇，a, b同號：$x=0$，$x=\pm \sqrt[m-n]{\frac{b}{a}}$，共3個相異實根。
(4) m, n奇，a, b異號：$x=0$，另兩根為虛數，僅1實根。
(5) m, n一奇一偶：例如m=4, n=3，得 $x^3(x - \frac{b}{a})=0$，僅2個相異實根。
故選(1)(3)。答案：(1)(3) 報錯
 ChatGPT DeepSeek

加最愛

106學測數學考科–09

設Γ為坐標平面上的圓，點(0,0)在Γ的外部且點(2,6)在Γ的內部。請選出正確的選項。
(1) Γ的圓心不可能在第二象限
(2) Γ的圓心可能在第三象限且此時Γ的半徑必定大於10
(3) Γ的圓心可能在第一象限且此時Γ的半徑必定小於10
(4) Γ的圓心可能在x軸上且此時圓心的x坐標必定小於10
(5) Γ的圓心可能在第四象限且此時Γ的半徑必定大於10。

答案

點(0,0)與(2,6)連線段的中垂線為 $x+3y=10$。圓心需在點(2,6)所在側的半平面 $x+3y>10$ 內。
(1) 第二象限部分區域可能滿足。
(2) 第三象限圓心，半徑需大於圓心到(0,0)距離，可能大於10，非必定。
(3) 第一象限圓心，半徑可能大於10。
(4) x軸上圓心，x坐標可能大於10。
(5) 第四象限圓心，因遠離(0,0)且靠近(2,6)，半徑需大於圓心到(0,0)距離，可能大於10，非必定。原解析認為(5)正確，但需注意「必定」二字。依原詳解，選(5)。答案：(5) 報錯
 ChatGPT DeepSeek

加最愛

106學測數學考科–10

坐標空間中有三直線 $ L_1 : \frac{x-1}{2} = \frac{y+1}{2} = \frac{z}{1} $，$ L_2 : \begin{cases} x-2y+2z=-4 \\ x+y-4z=5 \end{cases} $，$ L_3 : \begin{cases} x=-t \\ y=-2-t \\ z=4+4t \end{cases} $，t為實數。
請選出正確的選項。
(1) $ L_1$與$ L_2$的方向向量互相垂直
(2) $ L_1$與$ L_3$的方向向量互相垂直
(3)有一個平面同時包含$ L_1$與$ L_2$
(4)有一個平面同時包含$ L_1$與$ L_3$
(5)有一個平面同時包含$ L_2$與$ L_3$。

答案

$L_1$方向向量$\vec{v_1}=(2,2,1)$，$L_2$方向向量$\vec{v_2}=(2,2,1)$（與$L_1$平行），$L_3$方向向量$\vec{v_3}=(-1,-1,4)$。
(1) $\vec{v_1} \cdot \vec{v_2} = 9 \neq 0$，不垂直。
(2) $\vec{v_1} \cdot \vec{v_3} = 0$，垂直。
(3) $L_1$與$L_2$平行，可決定一平面。
(4) $L_1$與$L_3$交於一點，可決定一平面。
(5) $L_2$與$L_3$歪斜，無共同平面。
故選(2)(3)(4)。答案：(2)(3)(4) 報錯
 ChatGPT DeepSeek

加最愛

Saved articles