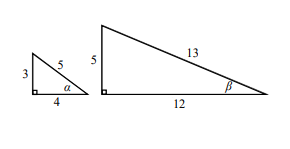
已知兩個直角三角形三邊長分別為3,4,5、5,12,13,\(\alpha\), \(\beta\)分別為它們的一角,如下圖所示。試選出正確的選項。
(1) \(\sin \alpha \gt \sin \beta \gt \sin 30^\circ\)
(2) \(\sin \alpha \gt \sin 30^\circ \gt \sin \beta\)
(3) \(\sin \beta \gt \sin \alpha \gt \sin 30^\circ\)
(4) \(\sin \beta \gt \sin 30^\circ \gt \sin \alpha\)
(5) \(\sin 30^\circ \gt \sin \alpha \gt \sin \beta\)
109學測數學
109學測數學考科-02
空間中有相異四點 \( A, B, C, D \),已知內積 \(\overset{\rightharpoonup}{AB} \cdot \overset{\rightharpoonup}{AC} = \overset{\rightharpoonup}{AB} \cdot \overset{\rightharpoonup}{AD}\)。試選出正確的選項。
(1) \(\overset{\rightharpoonup}{AB} \cdot \overset{\rightharpoonup}{CD} = 0\)
(2) \(\overset{\rightharpoonup}{AC} = \overset{\rightharpoonup}{AD}\)
(3) \(\overset{\rightharpoonup}{AB} \) 與 \(\overset{\rightharpoonup}{CD} \) 平行
(4) \(\overset{\rightharpoonup}{AD} \cdot \overset{\rightharpoonup}{BC} = 0\)
(5) \(A, B, C, D \) 四點在同一平面上。
\(\overset{\rightharpoonup}{AB} \cdot \overset{\rightharpoonup}{AC} = \overset{\rightharpoonup}{AB} \cdot \overset{\rightharpoonup}{AD} \Rightarrow \overset{\rightharpoonup}{AB} \cdot (\overset{\rightharpoonup}{AD} - \overset{\rightharpoonup}{AC}) = 0 \Rightarrow \overset{\rightharpoonup}{AB} \cdot \overset{\rightharpoonup}{CD} = 0\), 故選(1)。 報錯
ChatGPT DeepSeek
109學測數學考科-03
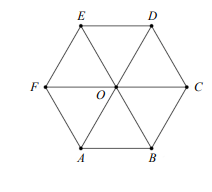
如圖所示,\(O\)為正六邊形之中心。試問下列哪個向量的終點P落在\(\triangle ODE\)內部(不含邊界)?
(1) \(\overset{\rightharpoonup}{OP} = \overset{\rightharpoonup}{OC} + \overset{\rightharpoonup}{OE}\)
(2) \(\overset{\rightharpoonup}{OP} = \frac{1}{4} \overset{\rightharpoonup}{OC} + \frac{1}{2} \overset{\rightharpoonup}{OE}\)
(3) \(\overset{\rightharpoonup}{OP} = -\frac{1}{4} \overset{\rightharpoonup}{OC} + \frac{1}{2} \overset{\rightharpoonup}{OE}\)
(4) \(\overset{\rightharpoonup}{OP} = \frac{1}{4} \overset{\rightharpoonup}{OC} – \frac{1}{2} \overset{\rightharpoonup}{OE}\)
(5) \(\overset{\rightharpoonup}{OP} = -\frac{1}{4} \overset{\rightharpoonup}{OC} – \frac{1}{2} \overset{\rightharpoonup}{OE}\)。
109學測數學考科-04
令 \(I = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}\), \(A = \begin{bmatrix} 1 & 1 \\ 3 & 4 \end{bmatrix}\), \(B = I + A + A^{-1}\),試選出代表 \(BA\) 的選項。
(1) \(\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}\)
(2) \(\begin{bmatrix} 6 & 0 \\ 0 & 6 \end{bmatrix}\)
(3) \(\begin{bmatrix} 4 & -1 \\ -3 & 1 \end{bmatrix}\)
(4) \(\begin{bmatrix} 1 & 1 \\ 3 & 4 \end{bmatrix}\)
(5) \(\begin{bmatrix} 6 & 6 \\ 18 & 24 \end{bmatrix}\)
109學測數學考科-05
試問數線上有多少個整數點與點 \(\sqrt{101}\) 的距離小於 5,但與點 \(\sqrt{38}\) 的距離大於 3?
(1) 1 個 (2) 4 個 (3) 6 個 (4) 8 個 (5) 10 個。
109學測數學考科-06
連續投擲一公正骰子兩次,設出現的點數依序為 \(a, b\)。試問發生 \(\log(a^2) + \log b \gt 1\) 的機率為多少?
(1) \(\frac{1}{3}\) (2) \(\frac{1}{2}\) (3) \(\frac{2}{3}\) (4) \(\frac{3}{4}\) (5) \(\frac{5}{6}\)。
109學測數學考科-07
坐標平面上,函數圖形 \(y = -\sqrt{3}x^3\) 上有兩點 \(P, Q\) 到原點距離皆為 1。已知點 \(P\) 坐標為 \((\cos\theta, \sin\theta)\),試問點 \(Q\) 坐標為何?
(1) \((\cos(-\theta), \sin(-\theta))\)
(2) \((-\cos\theta, \sin\theta)\)
(3) \((\cos(-\theta), -\sin\theta)\)
(4) \((-\cos\theta, \sin(-\theta))\)
(5) \((\cos\theta, -\sin\theta)\)。
109學測數學考科-08
有一個遊戲的規則如下:丟三顆公正骰子,若所得的點數恰滿足下列(A)或(B)兩個條件之一,可得到獎金100元;若兩個條件都滿足,則共得200元獎金;若兩個條件都不滿足,則無獎金。
(A)三個點數皆為奇數或者皆為偶數
(B)三個點數由小排到大為等差數列
若已知有兩顆骰子的點數分別為1,3,且所得獎金為100元,則未知的骰子點數可能為何?
(1) 2 (2) 3 (3) 4 (4) 5 (5) 6。
109學測數學考科-09
在坐標平面上,有一通過原點O的直線L,以及一半徑為2,圓心為原點O的圓T。P,Q為T上相異2點,且OP,OQ分別與L所夾的銳角皆為30°,試選出內積OP·OQ之值可能發生的選項。
(1) \( \frac{2\sqrt{3}}{5} \) (2) \(-2\sqrt{3}\) (3)0 (4) -2 (5) -4。