研究顯示：服用某藥物後，在使用者體內的藥物殘留量隨時間呈指數型衰退。已知在服用某藥物 2 小時後，體內仍殘留有該藥物的一半劑量，試問下列哪一選項正確？
(1)服用 3 小時後，體內仍殘留有該藥物的 \(\frac{1}{3}\) 劑量
(2)服用 4 小時後，體內仍殘留有該藥物的 \(\frac{1}{4}\) 劑量
(3)服用 6 小時後，體內仍殘留有該藥物的 \(\frac{1}{6}\) 劑量
(4)服用 8 小時後，體內仍殘留有該藥物的 \(\frac{1}{8}\) 劑量
(5)服用 10 小時後，體內仍殘留有該藥物的 \(\frac{1}{10}\) 劑量
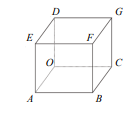如右圖，\( OABC – DEFG \) 為一正方體，試問向量外積 \( \overset{\rightharpoonup}{AD} \times \overset{\rightharpoonup}{AG} \) 與下列哪一個向量平行？
(1) \( \overset{\rightharpoonup}{AE} \)
(2) \( \overset{\rightharpoonup}{BE} \)
(3) \( \overset{\rightharpoonup}{CE} \)
(4) \( \overset{\rightharpoonup}{DE} \)
(5) \( \overset{\rightharpoonup}{OE} \)
設 \( a \in \{-6, -4, -2, 2, 4, 6\} \)，已知 \( a \) 為實係數三次多項式 \( f(x) \) 的最高次項係數，若函數 \( y=f(x) \) 的圖形與 x 軸交於三點，且其 x 坐標成首項為 \(-7\)，公差為 \( a \) 的等差數列。試問共有幾個 \( a \) 使得 \( f(0)>0 \)？
(1) 1 個 (2) 2 個 (3) 3 個 (4) 4 個 (5) 5 個
試問有多少個實數 \( x \) 滿足 \(\sin\left( x + \frac{\pi}{6} \right) = \sin x + \sin\frac{\pi}{6}\) 且 \( 0 \leq x \lt 2\pi \)？
(1) 1 個 (2) 2 個 (3) 3 個 (4) 4 個 (5) 5 個（含）以上
將1到50這50個正整數平分成甲乙兩組，每組各25個數，使得甲組的中位數比乙組的中位數小1。試問共有幾種分法？
(1) \(C_{25}^{50}\) (2) \(C_{24}^{48}\) (3) \(C_{12}^{24}\) (4) \((C_{12}^{24})^2\) (5) \(C_{24}^{48} \cdot C_{12}^{24}\)
在同一平面上，相距 \(7\) 公里的 \(A \cdot B\) 兩砲臺，\(A\) 在 \(B\) 的正東方。某次演習時，\(A\) 向西偏北 \(\theta\) 方向發射砲彈，\(B\) 則向東偏北 \(\theta\) 方向發射砲彈，其中 \(\theta\) 為銳角，觀測回報兩砲彈皆命中 9 公里外的同一目標 \(P\)。接著 \(A\) 改向西偏北 \(\frac{\theta}{2}\) 方向發射砲彈，彈著點為 \(9\) 公里外的點 \(Q\)。試問砲臺 \(B\) 與彈著點 \(Q\) 的距離 \(BQ\) 為何？
(1) 4 公里 (2) 4.5 公里 (3) 5 公里 (4) 5.5 公里 (5) 6 公里
今坐標平面上滿足 \(y = \log x\) 的點 \((x, y)\) 所成圖形為 \(\Gamma\)，試問滿足下列哪些關係式的 \((x, y)\) 所成圖形與 \(\Gamma\) 完全相同？
(1) \(y + \frac{1}{2} = \log (5x)\)
(2) \(2y = \log (x^2)\)
(3) \(3y = \log (x^3)\)
(4) \(x = 10^y\)
(5) \(x^3 = 10^{(y^3)}\)
對任一正整數\(n\geq 2\)，令\(T_n\)表示邊長為\(n,n+1,n+2\)的三角形。試選出正確的選項。
(1) \(T_n\)皆為銳角三角形
(2) \(T_2,T_3,T_4,\ldots,T_{10}\)的周長形成等差數列
(3) \(T_n\)的面積隨\(n\)增大而增大
(4) \(T_5\)的三高依序形成等差數列
(5) \(T_3\)的最大角大於\(T_2\)的最大角
某實驗室蒐集了大量的 \( A, B \)兩相似物種，記錄其身長為 \( x \)（單位：公分）與體重 \( y \)（單位：公克），得 \( A, B \)兩物種的平均身長分別為 \( x_A = 5.2, x_B = 6 \)，標準差分別為0.3, 0.1。令 \( A, B \)兩物種的平均體重分別為 \( y_A, y_B \)。若 \( A, B \)兩物種其體重 \( y \)對身長 \( x \)的迴歸直線分別為 \( L_A: y = 2x – 0.6, L_B: y = 1.5x + 0.4 \)，相關係數分別為0.6, 0.3。今發現一隻身長5.6公分，體重8.6公克的個體P，試選出正確的選項。
(1) \( y_A \lt y_B \)
(2) \( A \)物種的體重標準差小於 \( B \)物種的體重標準差
(3) 就A物種而言，個體P的體重與平均體重 \( y_A \)之差的絕對值大於一個標準差
(4) 點(5.6, 8.6)到直線L_A的距離小於其到直線L_B的距離
(5) 點(5.6, 8.6)與點 \((x_A, y_A)\)的距離小於其與點 \((x_B, y_B)\)的距離
坐標平面上有一正方形與一正六邊形，正方形在正六邊形的右邊。已知兩正多邊形都有一邊在 x 軸上，且正方形中心 A 與正六邊形中心 B 都在 x 軸的上方，且兩多邊形恰有一個交點 P，又知正方形的邊長為 6，而點 P 到 x 軸的距離為 \( 2\sqrt{3} \)。試選出正確的選項。
(1) 點 A 到 x 軸的距離大於點 B 到 x 軸的距離
(2) 正六邊形的邊長為 6
(3) \(\overset{\rightharpoonup}{BA} = (7, 3 – 2\sqrt{3})\)
(4) \(\overset{\rightharpoonup}{AP} \gt \sqrt{10}\)
(5) 直線 AP 斜率大於 \( -\frac{1}{\sqrt{3}} \)
