[題組:第19題到第21題] 將上題結果中的 r 改為 -r，可看出在日一地連心線上，位於地球公轉軌道內側、距離地心為 r 處，尚有一個可與地球同步繞日公轉的定點，稱為拉格朗日點 \( L_1 \)。依題幹所述，為了避免其他熱輻射源的干擾，以觀察廣闊範圍內來自宇宙各處的微弱紅外線信號，JWST的位置選擇 \( L_2 \)，比起 \( L_1 \) 有何優點？試舉出二項優點。（4分）
答案
111分科物理
111物理分科測驗–22
[題組:第22題到第24題] ◎二十世紀初期對於光電效應有許多不同的解釋，密立坎經由實驗證實愛因斯坦的光量子論，從而奠定了現代光電科技的基礎。現代生活中常見的太陽能板，能將太陽能轉換為電能，即是應用此一效應。令 \( h \) 代表普朗克常數，\( e \) 代表基本電荷。
假設 \( f \) 為光頻率，\( \lambda \) 為光波長，\( c \) 為光速，\( E \) 為光量子能量，則下列關係何者正確？（單選）
(A) \( E = \frac{hc^2}{\lambda} \)
(B) \( E = h\lambda \)
(C) \( E = h\lambda^2 \)
(D) \( E = hf \)
(E) \( E = hf^2 \)
111物理分科測驗–23
[題組:第22題到第24題]題號,題目,答案,解析
(1) 於作答區下方表格的元件圖例，繪製於如圖 11 所示的虛線方格中，並加以正確連接（注意接點的極性），使其成為光電效應實驗的電路圖。（2分）
(2) 承 (1)，若對同一金屬，選擇多種波長不同、但都能產生光電效應的入射光進行測量，則對於其中每種波長的入射光，必須改變何種物理量，使電路的電流發生何種情況？並取得哪個物理量的實驗數據，才能估計朗克常數對基本電荷的比值 h/e？（2分）
答案
111物理分科測驗–24
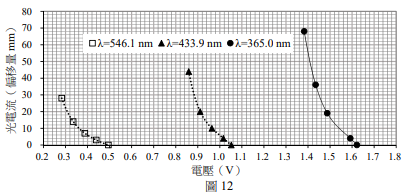
[題組:第22題到第24題] 圖 12 為密立根測得的光電效應數據。他使用光柵桿裝置來記錄錄光電流的大小，即是以前點偏移量（mm）代表光電流值。
（1）試依圖 12 中入射光波長 $\lambda = 546.1\ \mathrm{nm}$、$\lambda = 433.9\ \mathrm{nm}$、$\lambda = 365.0\ \mathrm{nm}$（頻率 $f = 5.49\times10^{14}\ \mathrm{Hz}$、$6.91\times10^{14}\ \mathrm{Hz}$、$8.22\times10^{14}\ \mathrm{Hz}$）的三組數據與其趨勢線，估測截止電壓（即遏止電位）$V_0$，將其填入作答區的表格第 3 列。（2 分）
（2）於方格紙中作 $V_0 – f$ 圖。（2 分）
（3）求出朗克常數與基本電荷的比值 $h/e$。（2 分）
答案
(1) $V_0$ 值：約 0.5 V、1.0 V、1.6 V
(2) 作 $V_0$ 對 $f$ 的圖，為直線
(3) $h/e \approx 4.13\times10^{-15}\ \mathrm{J\cdot s/C}$","
(1) 由圖 12 可見：
- $\lambda = 546.1\ \mathrm{nm}$ 時，電流降至零時電壓約為 0.5 V → $V_0 = 0.5\ \mathrm{V}$
- $\lambda = 433.9\ \mathrm{nm}$ 時，$V_0 \approx 1.0\ \mathrm{V}$
- $\lambda = 365.0\ \mathrm{nm}$ 時，$V_0 \approx 1.6\ \mathrm{V}$
(2) 以 $f$ 為橫軸、$V_0$ 為縱軸繪圖，應為直線。
(3) 由光電效應公式：
$eV_0 = hf - W_0$
整理得：
$V_0 = \frac{h}{e}f - \frac{W_0}{e}$
故 $V_0 - f$ 圖的斜率即為 $h/e$。
取兩點計算斜率：
- $f_1 = 5.49\times10^{14}\ \mathrm{Hz}, V_{01} = 0.5\ \mathrm{V}$
- $f_2 = 8.22\times10^{14}\ \mathrm{Hz}, V_{02} = 1.6\ \mathrm{V}$
斜率：
$\frac{\Delta V_0}{\Delta f} = \frac{1.6 - 0.5}{8.22\times10^{14} - 5.49\times10^{14}} = \frac{1.1}{2.73\times10^{14}} \approx 4.03\times10^{-15}\ \mathrm{V\cdot s}$
因此：
$\frac{h}{e} \approx 4.03\times10^{-15}\ \mathrm{J\cdot s / C}$
接近標準值 $4.13\times10^{-15}\ \mathrm{J\cdot s / C}$ 報錯
ChatGPT DeepSeek
111物理分科測驗–25
[題組:第25題到第26題]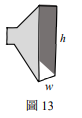 
◎聲波和光波一樣，在通過狹隘的開口往前傳播時都會出現繞射現象，而適用相同的繞射公式。圖13的矩形喇叭筒擴音器，是瑞士發明的，目的是在起大霧時，使喊話或警報能傳播到海岸邊一個大角度扇形水平區域內的船隻，避免將聲波能量浪費於向上或向下的傳播，w與h分別代表矩形開口的寬度與高度。當波發生繞射時，波強度出現極小值的角度θ，與波長λ和狹縫寬度的關係為 \( a \sin θ = nλ \quad (0 ≤ θ ≤ 90°, n = 1,2,3,\cdots) \) (1)式。比起光波，聲波的波長λ與狹縫寬度的比值通常較接近於1，因此上式不易出現n > 1的情況，以致聲波由開口向外傳播時主要會分布在張角為2θ的角度內，此處 \( \sin θ = \frac{λ}{a} \)，而張角是指以開口為頂點所張的角度。當 \( \frac{λ}{a} > 1 \) 時，(1)式無解，表示開口就近似於一個點，其向外傳播之聲波在開口前方的分布範圍（即張角），可達到180°。
已知人大力喊話時，主要不是透過基頻而是透過頻率約3kHz的泛音與噪音傳送資訊。而近似為矩形擴音器時，人的嘴巴相當於寬度約6cm的開口。若聲速為340m/s，則人張口大力喊話時，在其前方可涵蓋的水平扇形區域，其張角最接近下列何者？（單選）
(A)20° (B)30° (C)50° (D)90° (E)180°
答案
111物理分科測驗–26
[題組:第25題到第26題] (1)依據瑞立矩形開口擴音器的目的與聲波傳播的特性，建構一個關於瑞立矩形開口擴音器如何工作的理論模型，亦即說明該擴音器的寬度w與高度h，各與聲波波長λ具有什麼關係（需列出關係式），並預測要使聲波在水平方向的分散角度大於垂直方向的分散角度，w與h的大小關係應為何。（3分）
(2)承(1)：若要驗證該擴音器可達到聲音在水平與垂直方向的分散效果，在固定擴音器寬度w與高度h的情況下，需要測量何種數據？答題時若用到數學式或圖形，須說明所用各符號的定義。（3分）
答案
(1)由繞射公式 \( \sinθ = \frac{λ}{a} \)，水平分散角 \( 2θ_1 \)，垂直分散角 \( 2θ_2 \)。要使水平分散角大於垂直分散角，需 \( θ_1 > θ_2 \Rightarrow \frac{λ}{w} > \frac{λ}{h} \Rightarrow w < h \)。
(2)在距離擴音器L處測量聲音強度，在水平面上移動測量極小聲位置距離x，得 \( θ_1 = \tan^{-1}(\frac{x}{L}) \)；在垂直面上同理得 \( θ_2 \)。比較 \( θ_1 \) 和 \( θ_2 \) 即可驗證分散效果。 報錯
ChatGPT DeepSeek
