自然指考分科
113物理分科測驗24
[題組:24-26題]
◎一台具有三段變速系統的腳踏車(如圖10),其前齒盤的齒數為38齒,後齒盤組有相同轉軸但齒數分別為14、19與26齒的3個齒盤。鍵條套在前齒盤和後齒盤上,當前齒盤轉動1齒,後齒輪盤也跟著轉動1齒;且齒盤齒數與齒盤半徑成正比。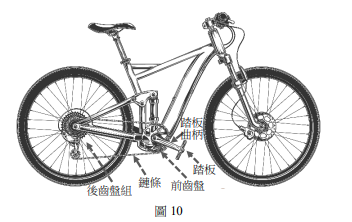
24 齒數為n的齒盤邊緣的切線速度定為\(v_n\),角速度定為\(\omega_n\),法線加速度(向心加速度)定為\(a_{Nu}\)。若變速系統將鍵條套在前齒盤與齒數19齒的後齒盤上,當前、後齒盤轉動時,下列敘述哪些正確?(多選)(5分)
(A)後齒盤:\(v_{26}/v_{14}=13/7\)
(B)後齒盤:\(\omega_{26}/\omega_{14}=7/13\)
(C)後齒盤:\(a_{N26}/a_{N14}=1\)
(D)前齒盤與後齒盤:\(\omega_{38}/\omega_{19}=1/2\)
(E)前齒盤與後齒盤:\(v_{38}/v_{19}=2\)
113物理分科測驗25
[題組:24-26題]
25 圖11為腳踏車驅動過程的示意圖:(i)騎士對踏板施力,經長度L的踏板曲柄對前齒盤的轉軸產生力矩;(ii)使前齒盤轉動並施力於鏈條上;(iii)鏈條上的力傳遞至後齒盤,使後齒盤轉動;(iv)後齒盤轉動時,施力於後輪使其轉動;(v)後輪與地面接觸點相對於地面靜止,地面施一反作用力於後輪,使腳踏車前進。若將腳踏車簡化為一質點,則下列有關腳踏車驅動過程的敘述哪些正確?(多選)(5分)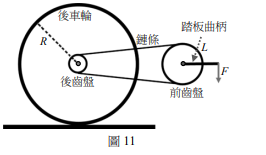
(A)在(i)中,踏板曲柄的長度L越長,則力矩越大
(B)在(ii)中,前齒盤的轉動動能會完全轉換為鏈條的動能
(C)在(iii)中,鏈條的張力對前齒盤與後齒盤的轉軸力矩和為零
(D)在(iv)中,後齒盤與後輪的轉動角速度相同
(E)在(v)中,地面對後輪的摩擦力方向與腳踏車前進方向相同
113物理分科測驗26
[題組:24-26題]
26 若腳踏車以等速度前進,且後輪半徑為33cm,當前齒盤轉速為60rpm(每分鐘轉數)時,腳踏車前進的速率為4.0m/s,則後齒盤的齒數為多少?(單選)(3分)
(A)14 (B)19 (C)26
114物理分科測驗01
2024年聯合國大會宣布2025年為國際量子科學與科技年(IYQ),以紀念海森堡及薛丁格分別於1925年及1926年提出全新量子力學數學表述方式,並與1900年代初期歐洲科學家、如普朗克、愛因斯坦、波耳、德布羅意等,共同奠定第一次量子革命的基礎,建立量子科技的發展。下列有關量子力學發展的敘述何者正確?
(A) 普朗克提出量子論成功解釋氫原子光譜的性質
(B) 德布羅意提出物質波說明波與粒子的二象性,僅適合於解釋電子的性質
(C) 波耳提出的原子模型,引入量子化能階概念說明原子核的組成與核衰變性質
(D) 當電子束穿過雙狹縫,各電子射到屏幕上的位置,可用量子力學精準預測
(E) 量子力學理論成功地描述電子在原子中的空間分布狀態及量子化能量的特性
114物理分科測驗02
114物理分科測驗03
1909年拉塞爾以α粒子對金箔作散射實驗而建立原子結構之基礎模型,下列對散射實驗結果的敘述,何者錯誤?
(A)以α粒子對金箔作散射實驗,是為了探究原子內部正電荷的分布是否均勻
(B)實驗結果發現大部分之α粒子可射穿金箔
(C)實驗結果發現有非常少數之α粒子被反彈回來
(D)實驗中出現反彈回來之α粒子可解釋為強作用對α粒子產生散射
(E)拉塞爾的散射實驗發現了原子核之存在
114物理分科測驗04
114物理分科測驗05
某生比較太陽系中行星與其最大衛星的資料,相關資料如表一,表中的衛星皆可視為繞其行星作等速圓周運動。
| 行星 | 行星質量 (kg) | 最大衛星 | 衛星質量 (kg) | 衛星繞行星週期 (day) | 衛星與行星平均距離 (km) |
| 地球 | \( 6.0 \times 10^{24} \) | 月球 | \( 7.4 \times 10^{22} \) | 約為28 | \( 3.6 \times 10^{5} \) |
| 土星 | ? | 泰坦衛星 | \( 1.3 \times 10^{23} \) | 約為14 | \( 1.2 \times 10^{6} \) |
試估算土星的質量約為多少 kg?
(A) \( 10^{23} \) (B) \( 10^{25} \) (C) \( 10^{27} \) (D) \( 10^{29} \) (E) \( 10^{31} \)