〈自然指考分科〉彙整頁面 - 第 45 頁，總計 53 頁

111物理分科測驗–24

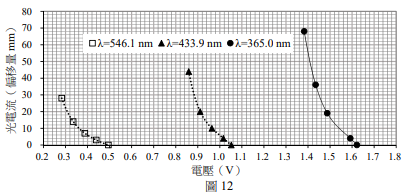
[題組:第22題到第24題] 圖 12 為密立根測得的光電效應數據。他使用光柵桿裝置來記錄錄光電流的大小，即是以前點偏移量（mm）代表光電流值。

（1）試依圖 12 中入射光波長 $\lambda = 546.1\ \mathrm{nm}$、$\lambda = 433.9\ \mathrm{nm}$、$\lambda = 365.0\ \mathrm{nm}$（頻率 $f = 5.49\times10^{14}\ \mathrm{Hz}$、$6.91\times10^{14}\ \mathrm{Hz}$、$8.22\times10^{14}\ \mathrm{Hz}$）的三組數據與其趨勢線，估測截止電壓（即遏止電位）$V_0$，將其填入作答區的表格第 3 列。（2 分）

（2）於方格紙中作 $V_0 – f$ 圖。（2 分）

（3）求出朗克常數與基本電荷的比值 $h/e$。（2 分）

[]

答案

(1) $V_0$ 值：約 0.5 V、1.0 V、1.6 V
(2) 作 $V_0$ 對 $f$ 的圖，為直線
(3) $h/e \approx 4.13\times10^{-15}\ \mathrm{J\cdot s/C}$","
(1) 由圖 12 可見：
- $\lambda = 546.1\ \mathrm{nm}$ 時，電流降至零時電壓約為 0.5 V → $V_0 = 0.5\ \mathrm{V}$
- $\lambda = 433.9\ \mathrm{nm}$ 時，$V_0 \approx 1.0\ \mathrm{V}$
- $\lambda = 365.0\ \mathrm{nm}$ 時，$V_0 \approx 1.6\ \mathrm{V}$

(2) 以 $f$ 為橫軸、$V_0$ 為縱軸繪圖，應為直線。

(3) 由光電效應公式：
$eV_0 = hf - W_0$
整理得：
$V_0 = \frac{h}{e}f - \frac{W_0}{e}$
故 $V_0 - f$ 圖的斜率即為 $h/e$。

取兩點計算斜率：
- $f_1 = 5.49\times10^{14}\ \mathrm{Hz}, V_{01} = 0.5\ \mathrm{V}$
- $f_2 = 8.22\times10^{14}\ \mathrm{Hz}, V_{02} = 1.6\ \mathrm{V}$

斜率：
$\frac{\Delta V_0}{\Delta f} = \frac{1.6 - 0.5}{8.22\times10^{14} - 5.49\times10^{14}} = \frac{1.1}{2.73\times10^{14}} \approx 4.03\times10^{-15}\ \mathrm{V\cdot s}$

因此：
$\frac{h}{e} \approx 4.03\times10^{-15}\ \mathrm{J\cdot s / C}$
接近標準值 $4.13\times10^{-15}\ \mathrm{J\cdot s / C}$ 報錯
 ChatGPT DeepSeek

加最愛

111物理分科測驗–25

[題組:第25題到第26題] ◎聲波和光波一樣，在通過狹隘的開口往前傳播時都會出現繞射現象，而適用相同的繞射公式。圖13的矩形喇叭筒擴音器，是瑞士發明的，目的是在起大霧時，使喊話或警報能傳播到海岸邊一個大角度扇形水平區域內的船隻，避免將聲波能量浪費於向上或向下的傳播，w與h分別代表矩形開口的寬度與高度。當波發生繞射時，波強度出現極小值的角度θ，與波長λ和狹縫寬度的關係為 $ a \sin θ = nλ \quad (0 ≤ θ ≤ 90°, n = 1,2,3,\cdots) $ (1)式。比起光波，聲波的波長λ與狹縫寬度的比值通常較接近於1，因此上式不易出現n > 1的情況，以致聲波由開口向外傳播時主要會分布在張角為2θ的角度內，此處 $ \sin θ = \frac{λ}{a} $，而張角是指以開口為頂點所張的角度。當 $ \frac{λ}{a} > 1 $ 時，(1)式無解，表示開口就近似於一個點，其向外傳播之聲波在開口前方的分布範圍（即張角），可達到180°。
已知人大力喊話時，主要不是透過基頻而是透過頻率約3kHz的泛音與噪音傳送資訊。而近似為矩形擴音器時，人的嘴巴相當於寬度約6cm的開口。若聲速為340m/s，則人張口大力喊話時，在其前方可涵蓋的水平扇形區域，其張角最接近下列何者？（單選）
(A)20° (B)30° (C)50° (D)90° (E)180°

[題組題]

答案

波長 $ λ = \frac{v}{f} = \frac{340}{3000} ≈ 0.113 $ m。開口寬度 a = 0.06 m，$ \frac{λ}{a} = \frac{0.113}{0.06} ≈ 1.88 > 1 $，故張角為180°，選(E)。報錯
 ChatGPT DeepSeek

加最愛

111物理分科測驗–26

[題組:第25題到第26題] (1)依據瑞立矩形開口擴音器的目的與聲波傳播的特性，建構一個關於瑞立矩形開口擴音器如何工作的理論模型，亦即說明該擴音器的寬度w與高度h，各與聲波波長λ具有什麼關係（需列出關係式），並預測要使聲波在水平方向的分散角度大於垂直方向的分散角度，w與h的大小關係應為何。（3分）
(2)承(1)：若要驗證該擴音器可達到聲音在水平與垂直方向的分散效果，在固定擴音器寬度w與高度h的情況下，需要測量何種數據？答題時若用到數學式或圖形，須說明所用各符號的定義。（3分）

[題組題]

答案

(1)由繞射公式 $ \sinθ = \frac{λ}{a} $，水平分散角 $ 2θ_1 $，垂直分散角 $ 2θ_2 $。要使水平分散角大於垂直分散角，需 $ θ_1 > θ_2 \Rightarrow \frac{λ}{w} > \frac{λ}{h} \Rightarrow w < h $。
(2)在距離擴音器L處測量聲音強度，在水平面上移動測量極小聲位置距離x，得 $ θ_1 = \tan^{-1}(\frac{x}{L}) $；在垂直面上同理得 $ θ_2 $。比較 $ θ_1 $ 和 $ θ_2 $ 即可驗證分散效果。報錯
 ChatGPT DeepSeek

加最愛

112物理分科測驗–01

下列選項的因次何者與能量因次不同？
(A)質量乘以速率平方
(B)力矩乘以角度
(C)壓力乘以體積
(D)衡量乘以時間
(E)電量乘以電壓

[單選題]

答案

能量因次為 $ [ML^2T^{-2}] $。(A) $ M(LT^{-1})^2 = ML^2T^{-2} $；(B)力矩 $ FL = ML^2T^{-2} $，角度無因次；(C)壓力 $ ML^{-1}T^{-2} $，體積 $ L^3 $；(D)衡量 $ MLT^{-1} $，乘以時間 $ T $ 得 $ ML $；(E)電量 $ IT $，電壓 $ ML^2T^{-3}I^{-1} $，乘積 $ ML^2T^{-2} $。故(D)因次不同。報錯
 ChatGPT DeepSeek

加最愛

112物理分科測驗–02

下列關於電磁波的敘述，何者正確？
(A)電磁波為微波
(B)可見光是電磁波，在真空中與介質中均以相同速率傳播
(C)電磁波與力學波一樣都有反射、折射、干涉與繞射現象
(D)相同強度的電磁波頻率越高，在真空中傳播的速率越快
(E)只要電場和磁場同時存在，便會產生交互作用而形成電磁波

[單選題]

答案

(A)錯：電磁波包含各種頻率。(B)錯：在介質中速率變慢。(C)對：電磁波具有波動四現象。(D)錯：真空中速率恆為 $ c $。(E)錯：需變化電場與變化磁場交互感應。選(C)。報錯
 ChatGPT DeepSeek

加最愛

112物理分科測驗–03

珠寶商使用最小刻度為 $1mg$ 的電子秤測量金飾質量 5 次，求得平均值為 $m_{AV}$，標準差為 SD。若以 $u_A $、$u_B$ 與 $u_C$ 分別代表標準的 A 類、B 類與組合不確定度，且已知分析過程計算機顯示 $m_{AV}$ 為 95.367823g，$u_C$ 為 0.35686524mg，則下列選項何者正確？
(A) $u_A = \frac{SD}{4}$
(B) $u_B = 1mg$
(C) $u_C = \frac{(u_A + u_B)}{2}$
(D)金飾質量的報告應為 $m_{AV} = 95.4g$，$u_C = 0.4mg$
(E)金飾質量的報告應為 $m_{AV} = 95.36782g$，$u_C = 0.36mg$

[單選題]

答案

(A)錯：$ u_A = \frac{SD}{\sqrt{5}} $。(B)錯：$ u_B = \frac{1}{2\sqrt{3}} \approx 0.29 $ mg。(C)錯：$ u_C = \sqrt{u_A^2 + u_B^2} $。(D)(E)：$ u_C $ 取 2 位有效數字 0.36 mg，$ m_{AV} $ 取至同一位 95.36782 g，選(E)。報錯
 ChatGPT DeepSeek

加最愛

112物理分科測驗–04

空間中有相距 $2d$ 的兩靜止點電荷，已知將此兩點電荷緩慢移近至相距 $d$ 靜止。需作功 $W$。若再將兩點電荷緩慢移近至相距 $d/5$ 靜止，則需再作多少功？
(A)10$W$
(B)8$W$
(C)5$W$
(D)4$W$
(E)$W$

[單選題]

答案

設兩同號電荷 +Q, +q。$ U_{2d} = \frac{kQq}{2d} $，$ U_d = \frac{kQq}{d} $，$ W = U_d - U_{2d} = \frac{kQq}{2d} $。$ U_{d/5} = \frac{5kQq}{d} $，再作功 $ W' = U_{d/5} - U_d = \frac{4kQq}{d} = 8W $，選(B)。報錯
 ChatGPT DeepSeek

加最愛

112物理分科測驗–05

某生設計了一個不需使用計時器而可量測重力加速度的實驗。他選用了一個彈力常數為 $k$，自然長度為 $l$，繁有質量為 $m$ 之質點的彈簧，使其作水平面之簡諧運動。再以一個擺長為 $L$，擺鐘不計體積，質量為 $M$ 的單擺，調整其擺長 $L$，使兩個系統之簡諧運動的週期相同，則其所測得的重力加速度量值為何？
(A) $\frac{lM}{k}$
(B) $\frac{Lm}{k}$
(C) $\frac{LM}{k}$
(D) $\frac{lk}{M}$
(E) $\frac{Lk}{m}$

[單選題]

答案

彈簧週期 $ T_s = 2\pi\sqrt{\frac{m}{k}} $，單擺週期 $ T_p = 2\pi\sqrt{\frac{L}{g}} $。令 $ T_s = T_p $ 得 $ \sqrt{\frac{m}{k}} = \sqrt{\frac{L}{g}} \Rightarrow g = \frac{Lk}{m} $，選(E)。報錯
 ChatGPT DeepSeek

加最愛

112物理分科測驗–06

某一雜技表演者用五顆相同的小球做單手拋球表演，由同一高度依次將各球略微偏離鉛直方向、向上拋出，當球回到原本被拋出的高度時，以同一隻手將球接住，然後水平移動到拋出點，再拋出，如圖1所示的逆時針軌跡。每次拋球的時間間隔固定為 $ \tau $，初速的鉛直分量皆為 $ v_0 $，各球的運動軌跡相同，形成連續的循環。過程中，在空中而不在手中的球至少有四顆。假設重力加速度的量值為 $ g $，且空氣阻力可忽略，則下列選項何者正確？
(A) $ v_0 $ 可以是 $ \frac{g\tau}{2} $
(B) $ v_0 $ 可以是 $ g\tau $
(C) 每一小球在空中的時間可以是 $ 3\tau $
(D) 小球在最高點時離拋出點的鉛直距離可以是 $ \frac{g\tau^2}{2} $
(E) 小球在最高點時離拋出點的鉛直距離一定大於 $ 2g\tau^2 $

[單選題]

答案

空中至少 4 顆球，故每球在空中時間 $ t $ 滿足 $ 4\tau < t < 5\tau $。鉛直上拋 $ t = \frac{2v_0}{g} $，故 $ 2g\tau < v_0 < \frac{5}{2}g\tau $，(A)(B)錯。$ t $ 不在 $ 3\tau $ 範圍，(C)錯。最高點 $ h = \frac{v_0^2}{2g} = \frac{g}{2}(\frac{t}{2})^2 $，代入 $ t $ 範圍得 $ 2g\tau^2 < h < \frac{25}{8}g\tau^2 $，(D)錯(E)對。報錯
 ChatGPT DeepSeek

加最愛

112物理分科測驗–07

在光電效應實驗中，若入射光頻率固定，僅增加光的強度，而其餘條件不變，則增加的是下列光子的哪個物理量？
(A) 單一光子的能量
(B) 單位時間入射的光子總數
(C) 單一光子的動量
(D) 光子速度
(E) 光子質量

[單選題]

答案

頻率固定則單一光子能量 $ E = hf $ 不變，(A)錯。光強度增加表示單位時間內光子數增加，(B)對。動量 $ p = \frac{h}{\lambda} $，波長不變故動量不變，(C)錯。真空中光速不變，(D)錯。光子靜質量為0，(E)錯。選(B)。報錯
 ChatGPT DeepSeek

加最愛

Saved articles