會考111數學

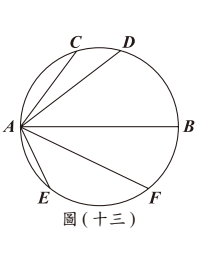
有一直徑為 $AB$ 的圓，且圓上有 $C$、$D$、$E$、$F$ 四點，其位置如圖(十三)所示。若 $AC= 6$，$AD= 8$，$AE= 5$，$AF= 9$，$AB= 10$，則下列弧長關係何者正確？
(A) $\overset{\frown}{AC}+ \overset{\frown}{AD}= \overset{\frown}{AB}$，$\overset{\frown}{AE}+ \overset{\frown}{AF}= \overset{\frown}{AB}$
(B) $\overset{\frown}{AC}+ \overset{\frown}{AD}= \overset{\frown}{AB}$，$\overset{\frown}{AE}+ \overset{\frown}{AF} \neq \overset{\frown}{AB}$
(C) $\overset{\frown}{AC}+ \overset{\frown}{AD} \neq \overset{\frown}{AB}$，$\overset{\frown}{AE}+ \overset{\frown}{AF}= \overset{\frown}{AB}$
(D) $\overset{\frown}{AC}+ \overset{\frown}{AD} \neq \overset{\frown}{AB}$，$\overset{\frown}{AE}+ \overset{\frown}{AF} \neq \overset{\frown}{AB}$

$\Delta ABC$ 的邊上有 $D$、$E$、$F$ 三點，各點位置如圖(十四)所示。若 $\angle B= \angle FAC$，$BD= AC$，$\angle BDE= \angle C$，則根據圖中標示的長度，求四邊形 $ADEF$ 與 $\Delta ABC$ 的面積比為何？
(A) $1: 3$
(B) $1: 4$
(C) $2: 5$
(D) $3: 8$

[題組:第24題到第25題]
表(一)、表(二)呈現 PA、PB 兩種日光燈管的相關數據,其中光通量用來衡量日光燈管的明亮程度。已知日光燈管的發光效率為光通量與功率的比值，甲、乙兩人根據表(一)、表(二)的資訊提出以下看法：
(甲) PA-20 日光燈管的發光效率比 PB-14 日光燈管高
(乙) PA 日光燈管中，功率較大的燈管其發光效率較高
關於甲、乙兩人的看法，下列敘述何者正確？
(A)甲、乙皆正確
(B)甲、乙皆錯誤
(C)甲正確，乙錯誤
(D)甲錯誤，乙正確

[題組:第24題到第25題]
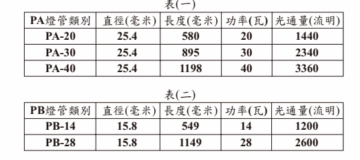
有一間公司請水電工程廠商安裝日光燈管，廠商提供兩種方案如表(三)所示。已知 $n$ 支功率皆為 $w$ 瓦的燈管都使用 $t$ 小時後消耗的電能（度）$= \dfrac{n }{1000}\times w \times t$，若每支燈管使用時間皆相同，且只考慮燈管消耗的電能並以每度 $5$ 元計算電費，則兩種方案相比，燈管使用時間至少要超過多少小時，採用省電方案所節省的電費才會高於兩者相差的施工費用？
(A) $12200$
(B) $12300$
(C) $12400$
(D) $12500$