下列何者為多項式 \(5x(5x-2)-4(5x-2)^2\) 的因式分解？
(A) \((5x-2)(25x-8)\)
(B) \((5x-2)(5x-4)\)
(C) \((5x-2)(-15x+8)\)
(D) \((5x-2)(-20x+4)\)
答案
會考數學
113會考數學考題_11
將 \(\frac{9}{4-\sqrt{7}}\) 化簡為 \(a+b\sqrt{7}\)，其中 \(a,b\) 為整數，求 \(a+b\) 之值為何？
(A) 5
(B) 3
(C) -9
(D) -15
答案
有理化：\(\frac{9}{4-\sqrt{7}}\times\frac{4+\sqrt{7}}{4+\sqrt{7}}=\frac{9(4+\sqrt{7})}{16-7}=\frac{9(4+\sqrt{7})}{9}=4+\sqrt{7}\)，\(a=4,b=1,a+b=5\)，故選(A)
113會考數學考題_12
甲、乙兩個二次函數分別為 \(y = (x + 20)^2 + 60\)、\(y = -(x – 30)^2 + 60\)，判斷下列敘述何者正確？
(A) 甲有最大值，且其值為 \(x = 20\) 時的 \(y\) 值
(B) 甲有最小值，且其值為 \(x = 20\) 時的 \(y\) 值
(C) 乙有最大值，且其值為 \(x = 30\) 時的 \(y\) 值
(D) 乙有最小值，且其值為 \(x = 30\) 時的 \(y\) 值
答案
113會考數學考題_13
圖（八）為阿威調整他的電腦畫面的解析度時看到的選項，當他從建議選項1920×1080調整成1400×1050時，由於比例改變（1920：1080÷1400：1050），畫面左右會出現黑色區域，當比例不變就不會有此問題。判斷阿威將他的電腦畫面解析度從1920×1080調整成下列哪一種時，畫面左右不會出現黑色區域？
(A) 1680×1050
(B) 1600×900
(C) 1440×900
(D) 1280×1024
答案
113會考數學考題_14
小玲搭飛機出國旅遊，已知她搭飛機產生的碳排放量為800公斤，為了彌補這些碳排放量，她決定上下班時從駕駛汽車改成搭公車。依據圖（九）的資訊，假設小玲每日上下班駕駛汽車或搭公車的來回總距離皆為20公里，則與駕駛汽車相比，她至少要改搭公車上下班幾天，減少產生的碳排放量才會超過她搭飛機產生的碳排放量？
(A) 310天
(B) 309天
(C) 308天
(D) 307天
答案
每日減少碳排放=\(20\times(0.17-0.04)=20\times0.13=2.6\)公斤，需要天數>\(\frac{800}{2.6}\approx307.69\)，故取308天，選(C)
113會考數學考題_15
甲、乙兩個最簡分數分別為 \(\frac{10}{a} \cdot \frac{18}{b}\)，其中 \(a \cdot b\) 為正整數。若將甲、乙通分化成相同的分母後，甲的分子變為 50，乙的分子變為 54，則下列關於 \(a\) 的敘述，何者正確？
(A) \(a\) 是 3 的倍數，也是 5 的倍數
(B) \(a\) 是 3 的倍數，但不是 5 的倍數
(C) \(a\) 是 5 的倍數，但不是 3 的倍數
(D) \(a\) 不是 3 的倍數，也不是 5 的倍數
答案
113會考數學考題_16
有研究報告指出，1880 年至 2020 年全球平均氣溫上升趨勢約為每十年上升 0.08℃。已知 2020 年全球平均氣溫為 14.88℃，假設未來的全球平均氣溫上升趨勢與上述趨勢相同，且每年上升的度數相同，則預估 2020 年之後第 \(x\) 年的全球平均氣溫為多少℃？（以 \(x\) 表示）
(A) 14.88 + 0.08x
(B) 14.88 + 0.008x
(C) 14.88 + 0.08 [\(x + (2020 – 1880)\)]
(D) 14.88 + 0.008 [\(x + (2020 – 1880)\)]
答案
113會考數學考題_17
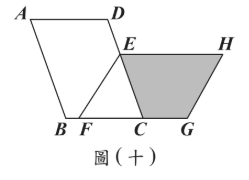
\(\triangle ABC\) 中，\(\angle B = 55^\circ\)，\(\angle C = 65^\circ\)。今分別以 \(B \cdot C\) 為圓心，\(BC\) 長為半徑畫圓 \(B\)、圓 \(C\)，關於 \(A\) 點位置，下列敘述何者正確？
(A) 在圓 \(B\) 外部，在圓 \(C\) 內部
(B) 在圓 \(B\) 外部，在圓 \(C\) 外部
(C) 在圓 \(B\) 內部，在圓 \(C\) 內部
(D) 在圓 \(B\) 內部，在圓 \(C\) 外部
答案
\(\angle A=60^\circ\)，在圓B中，\(\angle A\gt\angle C\)，故A在圓B外部；在圓C中，\(\angle A\lt\angle B\)，故A在圓C內部，選(A)
113會考數學考題_18
如圖（十），平行四邊形 \(ABCD\) 與平行四邊形 \(EFGH\) 全等，且 \(A \cdot B \cdot C \cdot D\) 的對應頂點分別是 \(H \cdot E \cdot F \cdot G\)，其中 \(E\) 在 \(DC\) 上，\(F\) 在 \(BC\) 上，\(C\) 在 \(FG\) 上。若 \(\overline{AB} = 7, \overline{AD} = 5, \overline{FC} = 3\)，則四邊形 \(ECGH\) 的周長為何？
(A) 21
(B) 20
(C) 19
(D) 18
答案
113會考數學考題_19
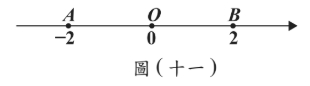圖（十一）的數線上有 \(A(-2) \cdot O(0) \cdot B(2)\) 三點。今打算在此數線上標示 \(P(p) \cdot Q(q)\) 兩點，且 \(p \cdot q\) 互為倒數；若 \(P\) 在 \(A\) 的左側，則下列敘述何者正確？
(A) \(Q\) 在 \(\overline{AO}\) 上，且 \(\overline{AQ} \lt \overline{OO}\)
(B) \(Q\) 在 \(\overline{AO}\) 上，且 \(\overline{AQ} \gt \overline{OO}\)
(C) \(Q\) 在 \(\overline{OB}\) 上，且 \(\overline{OQ} \lt \overline{QB}\)
(D) \(Q\) 在 \(\overline{OB}\) 上，且 \(\overline{OQ} \gt \overline{QB}\)
答案
P在A左側則\(p\lt -2\)，倒數\(q\)滿足\(-0.5\lt q\lt 0\)，Q在AO上且靠近O，故\(\overline{AQ}\gt\overline{OQ}\)，選(B)