四邊形 \(ABCD\) 中,\(E 、 F\) 兩點在 \(\overline{BC}\) 上,\(G\) 點在 \(\overline{AD}\) 上,各點位置如圖(十二)所示。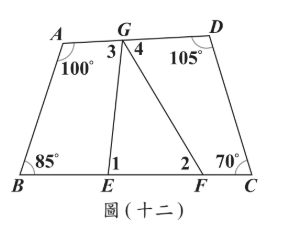 連接 \(\overline{GE} 、 GF\) 後,根據圖(十二)中標示的角與角度,判斷下列關係何者正確?
連接 \(\overline{GE} 、 GF\) 後,根據圖(十二)中標示的角與角度,判斷下列關係何者正確?
(A) \(\angle 1 + \angle 2 \lt \angle 3 + \angle 4\)
(B) \(\angle 1 + \angle 2 \gt \angle 3 + \angle 4\)
(C) \(\angle 1 + \angle 4 \lt \angle 2 + \angle 3\)
(D) \(\angle 1 + \angle 4 \gt \angle 2 + \angle 3\)
會考數學
113會考數學考題_21
113會考數學考題_22
如圖(十四),\(\triangle ABC\)內部有一點\(D\),且\(\triangle DAB\)、\(\triangle DBC\)、\(\triangle DCA\)的面積分別為5、4、3。若\(\triangle ABC\)的重心為\(G\),則下列敘述何者正確?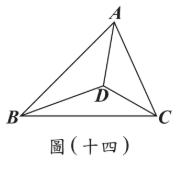
(A) \(\triangle GBC\)與\(\triangle DBC\)的面積相同,且\(DG\)與\(BC\)平行
(B) \(\triangle GBC\)與\(\triangle DBC\)的面積相同,且\(DG\)與\(BC\)不平行
(C) \(\triangle GCA\)與\(\triangle DCA\)的面積相同,且\(DG\)與\(AC\)平行
(D) \(\triangle GCA\)與\(\triangle DCA\)的面積相同,且\(DG\)與\(AC\)不平行
113會考數學考題_23
113會考數學考題_24
[題組:第24-25題]體重為衡量個人健康的重要指標之一,表(一)為成年人利用身高(公尺)計算理想體重(公斤)的三種方式,由於這些計算方式沒有考慮脂肪及肌肉重量占體重的比例,因此結果僅供參考。
| 女性理想體重 | 男性理想體重 | |
|---|---|---|
| 算法① | 身高×身高×22 | 身高×身高×22 |
| 算法② | (100×身高−70)×0.6 | (100×身高−80)×0.7 |
| 算法③ | (100×身高−158)×0.5+52 | (100×身高−170)×0.6+62 |
以下為甲、乙兩個關於成年女性理想體重的敘述:
(甲)有的女性使用算法①與算法②算出的理想體重會相同
(乙)有的女性使用算法②與算法③算出的理想體重會相同
對於甲、乙兩個敘述,下列判斷何者正確?
(A) 甲、乙皆正確
(B) 甲、乙皆錯誤
(C) 甲正確,乙錯誤
(D) 甲錯誤,乙正確
113會考數學考題_25
[題組:第24-25題]無論我們使用哪一種算法計算理想體重,都可將個人的實際體重歸類為表(二)的其中一種類別。
| 實際體重 | 類別 |
|---|---|
| 大於理想體重的120% | 肥胖 |
| 介於理想體重的110%~120% | 過重 |
| 介於理想體重的90%~110% | 正常 |
| 介於理想體重的80%~90% | 過輕 |
| 小於理想體重的80% | 消瘦 |
當身高 1.8 公尺的成年男性使用算法②計算理想體重並根據表(二)歸類,實際體重介於 70 × 90% 公斤至 70 × 110% 公斤之間會被歸類為正常。若將上述身高 1.8 公尺且實際體重被歸類為正常的成年男性,重新以算法③計算理想體重並根據表(二)歸類,則所有可能被歸類的類別為何?
(A) 正常
(B) 正常、過重
(C) 正常、過輕
(D) 正常、過重、過輕
算法②理想體重=\(0.7\times(100\times1.8-80)=70\),正常範圍63~77公斤
算法③理想體重=\(0.6\times(100\times1.8-170)+62=68\),對應63~77公斤的範圍為92.6%~113.2%,包含正常和過重,故選(B)
113會考數學考題_26
「健康飲食餐盤」是一種以圖畫呈現飲食指南的方式,圖畫中各類食物區塊的面積比,表示一個人每日所應攝取各類食物的份量比。某研究機構對於一般人如何搭配「穀類」、「蛋白質」、「蔬菜」、「水果」這四大類食物的攝取份量,以「健康標語」說明這四大類食物所應攝取份量的關係如圖(十七),並繪製了「健康飲食餐盤」如圖(十八)。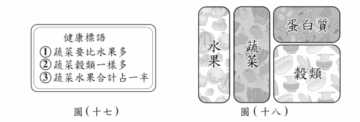 請根據上述資訊回答下列問題,完整寫出你的解題過程並詳細解釋:
請根據上述資訊回答下列問題,完整寫出你的解題過程並詳細解釋:
(1) 請根據圖(十七)的「健康標語」,判斷一個人每日所應攝取的「水果」和「蛋白質」份量之間的大小關係。
(2) 將圖(十八)的「健康飲食餐盤」簡化為一個矩形,且其中四大類食物的區塊皆為矩形,如圖(十九)所示。若要符合圖(十七)的「健康標語」,在紙上畫出圖(十九)的圖形,其中餐盤長為16公分,寬為10公分,則a、b是否可能同時為正整數?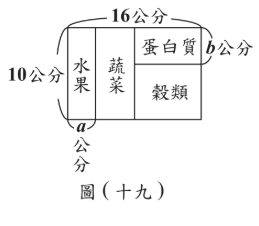
(1) 由標語「蔬菜份量比水果多,水果份量比蛋白質多」可得:蔬菜>水果>蛋白質
(2) 總面積=16×10=160平方公分
設穀類:蛋白質:蔬菜:水果=x:y:z:w
由標語得z>w>y
且x+y+z+w=160
由圖(十九)配置可得:
穀類面積=10a
蛋白質面積=10b
蔬菜面積=(16-a-b)×10
水果面積=(16-a)×10-蔬菜面積=10(16-a)-10(16-a-b)=10b
但水果面積應大於蛋白質面積,矛盾
因此a、b不可能同時為正整數
113會考數學考題_27
某教室內的桌子皆為同一款多功能桌,4張此款桌子可緊密拼接成中間有圓形鏤空的大圓桌,上視圖如圖(二十)所示,其外圍及鏤空邊界為一大一小的同心圓,其中大圓的半徑為80公分,小圓的半徑為20公分,且任兩張相鄰桌子接縫的延長線皆通過圓心。 為了有效運用教室空間,老師考慮了圖(二十一)及圖(二十二)兩種拼接此款桌子的方式。這兩種方式皆是將2張桌子的一邊完全貼合進行拼接。A、B兩點為圖(二十一)中距離最遠的兩個桌角,C、D兩點為圖(二十二)中距離最遠的兩個桌角,且CD與2張桌子的接縫EF相交於G點,G為EF中點。
為了有效運用教室空間,老師考慮了圖(二十一)及圖(二十二)兩種拼接此款桌子的方式。這兩種方式皆是將2張桌子的一邊完全貼合進行拼接。A、B兩點為圖(二十一)中距離最遠的兩個桌角,C、D兩點為圖(二十二)中距離最遠的兩個桌角,且CD與2張桌子的接縫EF相交於G點,G為EF中點。 請根據上述資訊及圖(二十一)、圖(二十二)中的標示回答下列問題,完整寫出你的解題過程並詳細解釋:
請根據上述資訊及圖(二十一)、圖(二十二)中的標示回答下列問題,完整寫出你的解題過程並詳細解釋:
(1) GF的長度為多少公分?
(2) 判斷CD與AB的長度何者較大?請說明理由。
(1) 由4張桌子拼成圓桌可知每張桌子為90度扇形的一部分
大圓半徑80cm,小圓半徑20cm
EF為兩張桌子接縫,G為EF中點
GF長度=\(\frac{1}{2}\times(80-20)=30\)公分
(2) AB為圖(二十一)最遠距離,CD為圖(二十二)最遠距離
計算可得AB長度較CD長度大
因為圖(二十一)拼接方式使對角線AB通過更多桌面區域,而圖(二十二)的CD被接縫分割
114會考數學考題_01
算式 \( 7^{10} \times 7^2 \div 7^4 \) 之值可用下列何者表示?
(A) \( 7^3 \)
(B) \( 7^5 \)
(C) \( 7^8 \)
(D) \( 7^{16} \)
114會考數學考題_02
計算 \( (5x^2 – 2x) – (4 – 3x) \) 的結果,與下列何者相同?
(A) \( 5x^2 – 3x \)
(B) \( 5x^2 + x – 4 \)
(C) \( 5x^2 – 5x + 4 \)
(D) \( 5x^2 – 5x – 4 \)