會考數學

圖（八）為貝可咖啡店的菜單，店家今日準備了120杯咖啡和100個三明治販售。若今日準備的餐點全部售出且收入共為8700元，則售出早餐組合的收入在下列哪一個範圍？
(A) 4300～4399元
(B) 4400～4499元
(C) 4500～4599元
(D) 4600～4699元

如圖（九），數線上由左至右有 \( A(a) \)、\( B(b) \)、\( C(c) \)、\( D(d) \)、\( E(e) \) 互點，且 \( AB = BC = CD = DE \)。若原點在 \( AE \) 上，且 \( |a| + |b| = |e| \)，則下列關於原點位置的敘述，何者正確？
(A) 在 \( BC \) 上且較接近 \( B \) 點
(B) 在 \( BC \) 上且較接近 \( C \) 點
(C) 在 \( CD \) 上且較接近 \( C \) 點
(D) 在 \( CD \) 上且較接近 \( D \) 點

如圖（十），\(\triangle ABC\) 中，\(D\) 點為 \(AB\) 的中點，\(E\) 點在 \(AB\) 上，\(F\) 點在 \(AC\) 上，且 \(EF // BC\)。若 \(AF = 7\)，\(FC = 3\)，則下列敘述何者正確？
(A) \(DE > EB\)，\(DF\) 與 \(EC\) 平行
(B) \(DE > EB\)，\(DF\) 與 \(EC\) 不平行
(C) \(DE < EB\)，\(DF\) 與 \(EC\) 平行
(D) \(DE < EB\)，\(DF\) 與 \(EC\) 不平行

圖（十一）是某種螺絲釘上螺紋的示意圖，圖中的虛線皆為水平線或鉛垂線，圖上標示出角度，也標示出水平線間或鉛垂線間的距離。根據圖中的標示，判斷此種螺絲釘的螺紋深度是螺紋間距的多少倍？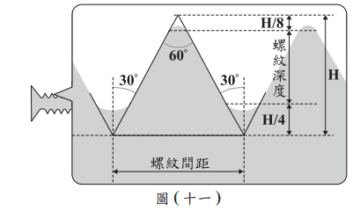
(A) \(\frac{5}{8}\)
(B) \(\frac{5}{16}\)
(C) \(\frac{5\sqrt{3}}{8}\)
(D) \(\frac{5\sqrt{3}}{16}\)

圖（十二）為金銀河影城的價目表。某社團16人去此影城看電影，打算以比賽獎金6000元購買電影票、爆米花與飲料。若要讓每人拿到一張電影票和一杯飲料，則最多可買多少盒爆米花？
(A) 3
(B) 4
(C) 5
(D) 6

圖（十三）為一張五邊形紙片 \( ABCDE \)，\( F \) 點在 \( CD \) 上，且以 \( BE \)、\( BF \)、\( FE \) 為摺線將紙片向內摺至同一平面後，\( A \)、\( C \)、\( D \) 恰重疊在同一點 \( P \)，如圖（十四）所示。若 \( BE > FE > BF \)，則根據圖（十四）中標示的角，判斷下列敘述何者正確？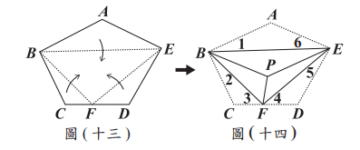
(A) \(\angle 3 + \angle 4 = 90^\circ\)，\(\angle 1 + \angle 2 > \angle 5 + \angle 6\)
(B) \(\angle 3 + \angle 4 = 90^\circ\)，\(\angle 1 + \angle 2 < \angle 5 + \angle 6\)
(C) \(\angle 3 + \angle 4 \neq 90^\circ\)，\(\angle 1 + \angle 2 > \angle 5 + \angle 6\)
(D) \(\angle 3 + \angle 4 \neq 90^\circ\)，\(\angle 1 + \angle 2 < \angle 5 + \angle 6\)

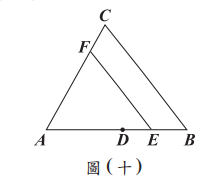
如圖（十五），\(\triangle ADG\) 的頂點 \( G \) 為 \(\triangle ABC\) 的重心，\(\overline{DG}\) 與 \(\overline{AB}\) 相交於 \( E \) 點。若 \(\overline{DE} : EG = 3:2, AE : EB = 3:4\)，則 \(\triangle ADG\) 面積為 \(\triangle ABC\) 面積的多少倍？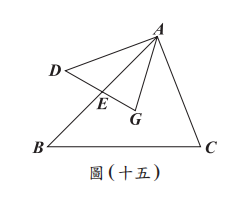
(A) \(\frac{5}{12}\)
(B) \(\frac{5}{14}\)
(C) \(\frac{5}{15}\)
(D) \(\frac{5}{21}\)