會考數學

如圖（十五），\(\triangle ADG\) 的頂點 \( G \) 為 \(\triangle ABC\) 的重心，\(\overline{DG}\) 與 \(\overline{AB}\) 相交於 \( E \) 點。若 \(\overline{DE} : EG = 3:2, AE : EB = 3:4\)，則 \(\triangle ADG\) 面積為 \(\triangle ABC\) 面積的多少倍？
(A) \(\frac{5}{12}\)
(B) \(\frac{5}{14}\)
(C) \(\frac{5}{15}\)
(D) \(\frac{5}{21}\)

如圖（十六），\(\triangle ABC\) 的三個頂點都在一圓上，固定 \( A \) 點將 \(\triangle ABC\) 依順時針方向旋轉，旋轉後的三角形為 \(\triangle AB’C’\)，且 \( B’ \) 會落在同一圓上，其中 \(\overline{AB}\) 與 \(\overline{AC’}\) 的夾角為 \( x^0 \)。若 \(\stackrel{\frown}{BC} = 54^\circ, \stackrel{\frown}{CA} = 62^\circ\)，則 \( x \) 值為何？
(A) 27
(B) 31
(C) 32
(D) 37

某民調公司訪問A市的成年民眾對於某項政策的態度，並依年齡分成3組。因受訪者的年齡分布與全體成年人口的年齡分布有落差，於是利用「調整倍率」讓調整後的結果更接近全體的民意，如表（二）所示。
表（二）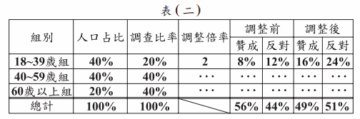

其中，
人口占比 = $\frac{該組人口總數}{全體成年人口總數} \times 100\% $
調查比率 = $\frac{該組受訪者數}{所有受訪者數} \times 100\% $
調整倍率 =$\frac{ 該組人口占比}{該組調查比率}$
調整前贊成（反對）的比率 = $\frac{該組受訪者中贊成（反對）人數}{所有受訪者數} \times 100\% $
調整後贊成（反對）的比率 = $該組調整前贊成（反對）的比率  \times  調整倍率$
表（二）中，全體成年人口有40%為18～39歲組，但受訪者中只有20%為18～39歲組，算出調整倍率為2。因此，分別將贊成與反對的比率8%、12%乘以2，變成16%、24%。整體結果調整前為贊成大於反對，調整後卻變成反對大於贊成。
請根據上述資訊回答下列問題，完整寫出你的解題過程並詳細解釋：
(1) 計算60歲以上組的調整倍率為何？
(2) 求40～59歲組與60歲以上組的調整前贊成比率分別為何？

商店中販賣一款包含 A、B 兩種圖案的藝術紙片組合包，形狀分別為 16 公分×5 公分、18 公分×5 公分的長方形，如圖（十七）所示。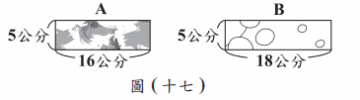小燦打算在不裁切紙片的情況下，將這兩種藝術紙片以緊密相鄰的方式貼成圖（十八）的長方形，其中奇數層為 A 圖案，偶數層為 B 圖案，且最後一層為 A 圖案，而相同圖案的藝術紙片皆為相同的方向。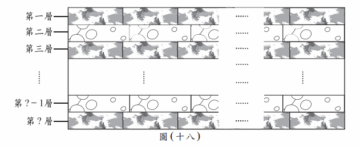
請根據上述資訊回答下列問題，完整寫出你的解題過程並詳細解釋：
(1) 以上述方式貼成的長方形，第一層最少有幾個$ A$ 圖案？
(2) 已知每個組合包中 $A、B$ 兩種圖案的藝術紙片數量比為 $4：3$，若小燦想購買一些組合包，貼成圖（十八）的長方形，其中第一層的 A 圖案數量與 (1) 求出之值相同，判斷他是否可能恰好把購買的藝術紙片用完？請說明理由。