有一底面為正方形的四角錐,其展開圖如下圖所示,
其中兩側面的三角形邊長為3,4,5 ,則此角錐的體積為 __________。（化為最簡根式）
[選填]
答案
三角形
104學測數學考科-19
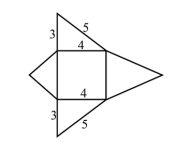
在空間中,一個斜面的「坡度」定義為斜面與水平
面夾角 \(\theta\) 的正切值 \(\tan\theta\) 。若一金字塔（底部為一正方形,四個斜面為等腰三角形）的每一個斜面的坡度皆為 \(\frac{2}{5}\) ,如圖。則相鄰斜面的夾角的餘弦函數的絕對值為 ________。（化為最簡分數）
[選填]
答案
\[
\tan\theta = \frac{OH}{EH} = \frac{2}{5},
\]
令 \(EH=5\)，\(OH=2\)，則 \(OE=\sqrt{29}\)，\(BE=5\)。
得
\[
OB = OA = OC = \sqrt{54},\quad AC=10\sqrt{2}.
\]
設 \(AG \perp OB\)，\(CG \perp OB\)，則 \(\angle AGC\) 即為二面角。
在 \(\triangle AOB\) 中，
\[
\cos\angle AOB = \frac{54+54-200}{2\times54} = \frac{2}{27}.
\]
又
\[
\frac{OG}{OA} = \frac{2}{27} \Rightarrow OG = \frac{2\sqrt{54}}{27}.
\]
於是
\[
AG^2 = OA^2 - OG^2 = 54 - \frac{8}{27} = \frac{1450}{27}.
\]
代入 \(\triangle AGC\) 的餘弦定理：
\[
|\cos\angle AGC| = \left| \frac{\frac{2900}{27} - 200}{\frac{1450}{27}} \right|
= \left| \frac{-\frac{2500}{27}}{\frac{1450}{27}} \right|
= \frac{25}{29}.
\]
107學測數學考科-01
給定相異兩點 \( A, B \)，試問空間中能使 \(\triangle PAB\) 成一正三角形的所有點 \( P \) 所成集合為下列哪一選項？
(1)兩個點
(2)一線段
(3)一直線
(4)一圓
(5)一平面。
答案
107學測數學考科-10
已知坐標平面上 \(\triangle ABC\)，其中 \(\overset{\rightharpoonup}{AB} = (-4,3)\)，且 \(\overset{\rightharpoonup}{AC} = \left( \frac{2}{5}, \frac{4}{5} \right)\)。試選出正確的選項。
(1) \(\overline{BC} = 5\)
(2) \(\triangle ABC\) 是直角三角形
(3) \(\triangle ABC\) 的面積為 \(\frac{11}{5}\)
(4) \(\sin B \gt \sin C\)
(5) \(\cos A \gt \cos B\)。
答案
(1) \( \overset{\rightharpoonup}{BC} = \overset{\rightharpoonup}{AC} - \overset{\rightharpoonup}{AB} = \left( \frac{22}{5}, -\frac{11}{5} \right) \)，長度 \( \frac{11\sqrt{5}}{5} \neq 5 \) ✗。
(2) \( \overline{AB}=5 \)，\( \overline{AC}=\frac{2\sqrt{5}}{5} \)，\( \overline{BC}=\frac{11\sqrt{5}}{5} \)，檢查得 \( \overline{AC}^2 + \overline{BC}^2 = \frac{4}{5} + \frac{121}{5} = 25 = \overline{AB}^2 \) ✓。
(3) 面積 \( \frac{1}{2} \times \frac{2\sqrt{5}}{5} \times \frac{11\sqrt{5}}{5} = \frac{11}{5} \) ✓。
(4) \( \sin B = \frac{\overline{AC}}{\overline{AB}} = \frac{2\sqrt{5}}{25} \)，\( \sin C = 1 \)，故 \( \sin B \lt \sin C \) ✗。
(5) \( \cos A = \frac{\overset{\rightharpoonup}{AB} \cdot \overset{\rightharpoonup}{AC}}{5 \cdot \frac{2\sqrt{5}}{5}} = \frac{-8/5+12/5}{2\sqrt{5}} = \frac{4/5}{2\sqrt{5}} = \frac{2}{5\sqrt{5}} \)，\( \cos B = \frac{\overset{\rightharpoonup}{BA} \cdot \overset{\rightharpoonup}{BC}}{5 \cdot \frac{11\sqrt{5}}{5}} = \frac{ (4,-3) \cdot (22/5,-11/5) }{11\sqrt{5}} = \frac{88/5+33/5}{11\sqrt{5}} = \frac{121/5}{11\sqrt{5}} = \frac{11}{5\sqrt{5}} \)，故 \( \cos A \lt \cos B \) ✗。
故選(2)(3)。答案：(2)(3)
109學測數學考科-01
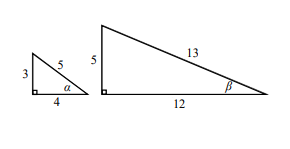
已知兩個直角三角形三邊長分別為3,4,5、5,12,13，\(\alpha\), \(\beta\)分別為它們的一角，如下圖所示。試選出正確的選項。
(1) \(\sin \alpha \gt \sin \beta \gt \sin 30^\circ\)
(2) \(\sin \alpha \gt \sin 30^\circ \gt \sin \beta\)
(3) \(\sin \beta \gt \sin \alpha \gt \sin 30^\circ\)
(4) \(\sin \beta \gt \sin 30^\circ \gt \sin \alpha\)
(5) \(\sin 30^\circ \gt \sin \alpha \gt \sin \beta\)
答案
109學測數學考科-13
如示意圖，四面體 \( OABC \) 中，\( \triangle OAB \) 和 \( \triangle OAC \) 均為正三角形，\( \angle BOC = 30^\circ \)。試選出正確的選項。
(1) \( BC \gt OC \)
(2) \( \triangle OBC \) 是等腰三角形
(3) \( \triangle OBC \) 的面積大於 \( \triangle OAB \) 的面積
(4) \( \angle CAB = 30^\circ \)
(5) 平面 \( OAB \) 和平面 \( OAC \) 的夾角（以銳角計）小於 \( 30^\circ \)。
答案
109學測數學考科-G
設計師為天文館設計以不銹鋼片製成的月亮形狀，其中有一款設計圖如右圖所示：圖中，圓弧 \( QRT \) 是一個以 \( O \) 點為圓心、\( OT \) 為直徑的半圓，\( OT = 2\sqrt{3} \)。圓弧 \( QST \) 的圓心在 \( P \) 點，\( PQ = PT = 2 \)。圓弧 \( QRT \) 與圓弧 \( QST \) 所圈出的灰色區域 \( QRTSQ \) 即為某一天所見的月亮形狀。設此灰色區域的面積為 \( a\pi + \sqrt{b} \)，其中 \( \pi \) 為圓周率，\( a \) 為有理數，\( b \) 為整數，則 \( a = \) __________（化為最簡分數），\( b = \) __________。
[選填題]
答案
114學測自然考科45
110學測數學考科_03
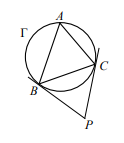如右圖，\(\triangle ABC\) 為銳角三角形，\( P \) 為 \(\triangle ABC\) 外接圓 \( \Gamma \) 外的一點，且 \( PB \) 與 \( PC \) 都與圓 \( \Gamma \) 相切。設 \(\angle BPC = \theta\)，試問 \( \cos A \) 的值為下列哪一個選項？
(1) \(\sin 2\theta\)
(2) \(\frac{\sin \theta}{2}\)
(3) \(\sin \frac{\theta}{2}\)
(4) \(\frac{\cos \theta}{2}\)
(5) \(\cos \frac{\theta}{2}\)
答案
連接圓心 O，則 \(\angle OBP = \angle OCP = 90^\circ\)，四邊形 OBPC 中，\(\angle BOC = 360^\circ - 90^\circ - 90^\circ - \theta = 180^\circ - \theta\)。圓周角 \(\angle A = \frac{1}{2} \angle BOC = 90^\circ - \frac{\theta}{2}\)，故 \(\cos A = \cos(90^\circ - \frac{\theta}{2}) = \sin \frac{\theta}{2}\)。(3)
110學測數學考科_04
設 \( a \) 與 \( b \) 都是平面上不為零的向量。若 \( 2\overset{\rightharpoonup}{a} + \overset{\rightharpoonup}{b} \) 與 \( \overset{\rightharpoonup}{a} + 2\overset{\rightharpoonup}{b} \) 所張成的三角形面積為 \( 6 \)，則 \( 3\overset{\rightharpoonup}{a} + \overset{\rightharpoonup}{b} \) 與 \( \overset{\rightharpoonup}{a} + 3\overset{\rightharpoonup}{b} \) 所張成的三角形面積為下列哪一個選項？
(1) 8
(2) 9
(3) 12
(4) 13.5
(5) 16
答案
設 \( a, b \) 所張成的平行四邊形面積為 \( \Delta \)，則 \( 2a+b \) 與 \( a+2b \) 所張成的平行四邊形面積為 \( \begin{vmatrix} 2 & 1 \\ 1 & 2 \end{vmatrix} \Delta = 3\Delta \)，三角形面積為 \( \frac{1}{2} \times 3\Delta = 6 \)，得 \( \Delta = 4 \)。\( 3a+b \) 與 \( a+3b \) 所張成的平行四邊形面積為 \( \begin{vmatrix} 3 & 1 \\ 1 & 3 \end{vmatrix} \Delta = 8 \times 4 = 32 \)，三角形面積為 \( \frac{1}{2} \times 32 = 16 \)。(5)