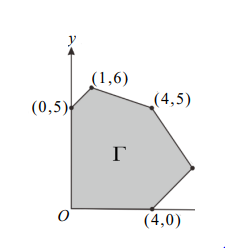
在坐標平面上給定三點 \(A(1,0), B(0,1), C(-1,0)\),令 \(\Gamma\) 為 \(\triangle ABC\) 經矩陣 \(T=\begin{bmatrix} 3 & 0 \\ a & 1 \end{bmatrix}\) 變換後的圖形,其中 \(a\) 為實數。試選出正確的選項。
(1) 若 \(a=0\),則 \(\Gamma\) 為等腰直角三角形
(2) \(\triangle ABC\) 的邊上至少有兩點經 \(T\) 變換後坐標不變
(3) \(\Gamma\) 必有部分落在第四象限
(4) 平面上找到一個圖形 \(\Omega\) 經 \(T\) 變換後為 \(\triangle ABC\)
(5) \(\Gamma\) 的面積為定值
三角形
105指考數學乙試題-07
坐標平面上 \( O \) 為原點,\( P \) 點坐標為 (1,0),直線 \( L \) 的方程式為 \( x-2y=-4 \)。請選出正確的選項。
(1) 在直線 \( L \) 上可以找到一點 \( A \),滿足向量 \( \overset{\rightharpoonup}{OP} \) 與 \( \overset{\rightharpoonup}{OA} \) 平行
(2) 在直線 \( L \) 上可以找到一點 \( B \),滿足向量 \( \overset{\rightharpoonup}{OP} \) 與 \( \overset{\rightharpoonup}{OB} \) 垂直
(3) 在直線 \( L \) 上可以找到一點 \( C \),滿足向量 \( \overset{\rightharpoonup}{OC} \) 與 \( \overset{\rightharpoonup}{PC} \) 垂直
(4) 在直線 \( L \) 上可以找到一點 \( D \),滿足 \( PD=2 \)
(5) 在直線 \( L \) 上可以找到一點 \( E \),滿足 \( \Delta EOP \) 為等腰三角形
\(L: x-2y=-4 \Rightarrow y=\frac{x+4}{2}\)。
(1) \( \overset{\rightharpoonup}{OP} = (1,0)\),平行意味著 \( \overset{\rightharpoonup}{OA} = k(1,0)\),即 y=0,代入 L 得 x=-4,A=(-4,0) 在 L 上,正確。
(2) 垂直則內積 0,設 B=(x,(x+4)/2),\( \overset{\rightharpoonup}{OB} \cdot \overset{\rightharpoonup}{OP} = x = 0\),得 B=(0,2) 在 L 上,正確。
(3) \( \overset{\rightharpoonup}{OC} \cdot \overset{\rightharpoonup}{PC} = 0\),設 C=(t,(t+4)/2),\( \overset{\rightharpoonup}{OC} = (t,(t+4)/2)\),\( \overset{\rightharpoonup}{PC} = (t-1,(t+4)/2)\),內積 \(t(t-1) + \frac{(t+4)^2}{4} = 0\),化簡得 \(4t^2-4t + t^2+8t+16 = 5t^2+4t+16=0\),判別式 16-320<0,無實數解,錯誤。
(4) 設 D=(t,(t+4)/2),\(PD^2 = (t-1)^2 + ((t+4)/2)^2 = 4\),化簡得 \(4(t^2-2t+1) + (t^2+8t+16) = 5t^2+20=0\)? 檢查:乘4:\(4(t-1)^2 + (t+4)^2 = 4(t^2-2t+1) + (t^2+8t+16) = 5t^2+0t+20 = 4\times 4=16\)? 我算錯。正確:\( (t-1)^2 + \frac{(t+4)^2}{4} = 4\),乘以4:\(4(t^2-2t+1) + (t^2+8t+16) = 5t^2+0t+20 = 16\),得 \(5t^2= -4\) 無解,錯誤。
(5) 等腰三角形 EOP:可能 EO=EP 或 EO=OP 或 EP=OP。OP=1。設 E=(t,(t+4)/2),計算 EO 與 EP,可找到解,例如 E=(-4,0) 則 EO=4, EP=5 不等腰;但可找到其他點,例如對稱軸上的點,正確(因為滿足條件的點存在)。
答案為 (1)(2)(5)。
109指考數學乙(補考)試題-02
在坐標平面上,\( O \) 為原點,考慮直線 \( L_1: 5x+3y=5 \) 與直線 \( L_2: 3x+2y=6-2a \),其中 \( a \) 為實數。若直線 \( L: 2x+y=3 \) 分別與直線 \( L_1 \) 及直線 \( L_2 \) 交於點 \( A \) 及點 \( B \),則三角形 \( OAB \) 的面積為下列哪一個選項?
(1) \( \frac{1}{2} |a-2| \)
(2) \( |a-2| \)
(3) \( 2|a-2| \)
(4) \( 3|a-2| \)
(5) \( 6|a-2| \)
求A點:解 \( \begin{cases} 5x+3y=5 \\ 2x+y=3 \end{cases} \),得 \( x=4 \),\( y=-5 \),故 \( A(4,-5) \)
求B點:解 \( \begin{cases} 3x+2y=6-2a \\ 2x+y=3 \end{cases} \),得 \( x=2a \),\( y=3-4a \),故 \( B(2a,3-4a) \)
三角形OAB面積 = \( \frac{1}{2} |x_A y_B - x_B y_A| = \frac{1}{2} |4(3-4a) - 2a(-5)| = \frac{1}{2} |12-16a+10a| = \frac{1}{2} |12-6a| = 3|2-a| = 3|a-2| \)
答案:(4)
109指考數學乙試題-_A
109學測社會試題-22
某地的警察組成有歐籍、印度籍、華籍,以及特別從山東威海衛招募來的人員,分別以ABCD編號。其中印度籍警察包著頭巾,華籍警察戴著三角形竹帽,穿綠色制服。當地孩童以「ABCD,大頭綠衣,追賊不到,吹嗶嗶!」來形容警察。這些孩童最可能是:
(A)在英國殖民統治香港時的華人小孩
(B)在德國轄下膠州灣生活的華人小孩
(C)在雅加達經商貿易的華僑家庭小孩
(D)在舊金山建造鐵路的華工家庭小孩
106學測自然試題-53
鑽石與石墨是碳的共價網狀固體。其中,鑽石質地堅硬,而石墨是易脆的物質。
下列有關兩者的敘述,哪些正確?(應選3項)
(A)石墨具有導電性,鑽石則否
(B)鑽石與石墨都是高熔點的固體
(C)鑽石是三維網狀排列,而石墨是二維層狀排列
(D)鑽石的每個碳原子連接三個碳原子,而石墨的每個碳原子連接四個碳原子
(E)鑽石中碳原子間連接形成的幾何結構為三角形,而石墨中碳原子間連接形成的幾何結構為四面體形
114分科測驗數學乙考科試卷-08
平面上三角形ABC,\(\angle A=91^\circ\)、\(\angle C=29^\circ\),令\(\overline{BC}=a\)、\(\overline{CA}=b\)、\(\overline{AB}=c\),試選出正確的選項?
(1) \(a^2\gt b^2+c^2\)
(2) \(\frac{c}{a}\gt\sin29^\circ\)
(3) \(\frac{b}{a}\gt\cos29^\circ\)
(4) \(\frac{a^2+b^2-c^2}{ab}\lt\sqrt{3}\)
(5) 外接圓半徑小於c
已知三角形 \(ABC\) 中:
\[
\angle A = 91^\circ, \quad \angle C = 29^\circ, \quad \angle B = 60^\circ
\]
(因為 \(180^\circ - 91^\circ - 29^\circ = 60^\circ\))
邊長:
\[
BC = a, \quad CA = b, \quad AB = c
\]
(即 \(a\) 對 \(\angle A\),\(b\) 對 \(\angle B\),\(c\) 對 \(\angle C\))
---
**(1) \( a^2 > b^2 + c^2 \)**
由餘弦定理:
\[
a^2 = b^2 + c^2 - 2bc\cos A
\]
\(\cos 91^\circ < 0\),所以 \(-2bc\cos A > 0\),因此
\[
a^2 > b^2 + c^2
\]
✅ 正確。
---
**(2) \( \frac{c}{a} > \sin 29^\circ \)**
正弦定理:
\[
\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = 2R
\]
所以
\[
\frac{c}{a} = \frac{\sin C}{\sin A} = \frac{\sin 29^\circ}{\sin 91^\circ}
\]
\(\sin 91^\circ \approx \sin 90^\circ = 1\),實際略大於 1(\(\sin 91^\circ \approx 0.99985\)),所以
\[
\frac{c}{a} \approx 0.99985^{-1} \times \sin 29^\circ \approx 1.00015 \times 0.4848 \approx 0.48487
\]
而 \(\sin 29^\circ \approx 0.4848\),比較:
\[
\frac{c}{a} \approx 0.48487 > 0.4848
\]
✅ 正確(雖然很接近,但確實大於)。
---
**(3) \( \frac{b}{a} > \cos 29^\circ \)**
\[
\frac{b}{a} = \frac{\sin B}{\sin A} = \frac{\sin 60^\circ}{\sin 91^\circ} \approx \frac{0.866025}{0.99985} \approx 0.86615
\]
\(\cos 29^\circ \approx 0.87462\),比較:
\[
0.86615 < 0.87462
\]
❌ 錯誤。
---
**(4) \( \frac{a^2 + b^2 - c^2}{ab} < \sqrt{3} \)**
由餘弦定理:
\[
\cos C = \frac{a^2 + b^2 - c^2}{2ab}
\]
所以
\[
\frac{a^2 + b^2 - c^2}{ab} = 2\cos C = 2\cos 29^\circ \approx 2 \times 0.87462 \approx 1.74924
\]
\(\sqrt{3} \approx 1.732\),比較:
\[
1.74924 > 1.732
\]
❌ 錯誤。
---
**(5) 外接圓半徑小於 \(c\)**
外接圓半徑 \(R = \frac{a}{2\sin A} \approx \frac{a}{2 \times 0.99985} \approx 0.500075 \times a\)
由正弦定理:
\[
c = 2R \sin C \implies R = \frac{c}{2\sin C} = \frac{c}{2 \times 0.4848} \approx \frac{c}{0.9696} \approx 1.0314 \times c
\]
等等,這裡要小心:題目給的 \(a,b,c\) 是邊長,\(R\) 是固定值。
用 \(a = 2R\sin A\),\(c = 2R\sin C\)。
比較 \(R\) 與 \(c\):
\[
c = 2R\sin C \implies \frac{R}{c} = \frac{1}{2\sin C} \approx \frac{1}{0.9696} \approx 1.0314
\]
所以 \(R \approx 1.0314 \times c > c\),因此 \(R < c\) 不成立。
❌ 錯誤。
---
**正確選項:** (1)、(2)
\[
\boxed{12}
\]
105指考數學甲試題-03
假設三角形 \(ABC\) 的三邊長分別為\(\overline{AB}=5\)、\(BC = 8\)、\(AC = 6\)。請選出和向量\(\overrightarrow{AB}\)的內積為最大的選項。
(1)\(\overset{\rightharpoonup}{AC}\)
(2)\(\overset{\rightharpoonup}{CA}\)
(3)\(\overset{\rightharpoonup}{BC}\)
(4)\(\overset{\rightharpoonup}{CB}\)
(5)\(\overset{\rightharpoonup}{AB}\)
根據向量內積公式\(\overrightarrow{a}\cdot\overrightarrow{b}=\vert\overrightarrow{a}\vert\vert\overrightarrow{b}\vert\cos\theta\)(\(\theta\)為\(\overrightarrow{a}\)與\(\overrightarrow{b}\)的夾角)。
由餘弦定理\(\cos A=\frac{AB^{2}+AC^{2}-BC^{2}}{2AB\cdot AC}=\frac{25 + 36 - 64}{2\times5\times6}=-\frac{1}{20}\);
\(\cos B=\frac{AB^{2}+BC^{2}-AC^{2}}{2AB\cdot BC}=\frac{25 + 64 - 36}{2\times5\times8}=\frac{53}{80}\);
\(\cos C=\frac{AC^{2}+BC^{2}-AB^{2}}{2AC\cdot BC}=\frac{36 + 64 - 25}{2\times6\times8}=\frac{75}{96}=\frac{25}{32}\)。
\(\overrightarrow{AB}\cdot\overrightarrow{AC}=\vert\overrightarrow{AB}\vert\vert\overrightarrow{AC}\vert\cos A=5\times6\times(-\frac{1}{20})=-\frac{3}{2}\);
\(\overrightarrow{AB}\cdot\overrightarrow{CA}=-\overrightarrow{AB}\cdot\overrightarrow{AC}=\frac{3}{2}\);
\(\overrightarrow{AB}\cdot\overrightarrow{BC}=\vert\overrightarrow{AB}\vert\vert\overrightarrow{BC}\vert\cos(\pi - B)=-5\times8\times\frac{53}{80}=-\frac{53}{2}\);
\(\overrightarrow{AB}\cdot\overrightarrow{CB}=-\overrightarrow{AB}\cdot\overrightarrow{BC}=\frac{53}{2}\);
\(\overrightarrow{AB}\cdot\overrightarrow{AB}=\vert\overrightarrow{AB}\vert^{2}=25\)。
比較可得\(\overrightarrow{AB}\cdot\overrightarrow{CB}\)最大。
答案為(4)。
106指考數學甲試題–B
坐標平面上有三條直線\(L\)、\(L_1\)、\(L_2\),其中\(L\)為水平線,\(L_1\)、\(L_2\)的斜率分別為\(\frac{3}{4}\)、\(-\frac{4}{3}\)。已知\(L\)被\(L_1\)、\(L_2\)所截出的線段長為30,則\(L\)、\(L_1\)、\(L_2\)所決定的三角形的面積為____。
[選填題]設直線 \( L: y = k \),與 \( L_1: 3x-4y=0 \)、\( L_2: 4x+3y=0 \) 的交點分別為 \( A、B \):
- 代入 \( L_1 \) 得 \( A\left(\frac{4k}{3}, k\right) \);
- 代入 \( L_2 \) 得 \( B\left(-\frac{3k}{4}, k\right) \)。
計算 \( \overline{AB} \) 的長度:
\[
\overline{AB} = \frac{4k}{3} - \left(-\frac{3k}{4}\right) = \frac{25k}{12}
\]
由 \( \overline{AB}=30 \),得:
\[
\frac{25k}{12}=30 \implies k=\frac{72}{5}
\]
故 \( \triangle OAB \) 的面積為:
\[
\text{面積} = \frac{1}{2} \times \overline{AB} \times k = \frac{1}{2} \times 30 \times \frac{72}{5} = 216
\]
106指考數學甲試題–C
坐標平面上,\(x\)坐標與\(y\)坐標均為整數的點稱為格子點。令\(n\)為正整數,\(T_n\)為平面上以直線\(y=\frac{-1}{2n}x + 3\),以及\(x\)軸、\(y\)軸所圍成的三角形區域(包含邊界),而\(a_n\)為\(T_n\)上的格子點數目,則\(\lim_{n \to \infty}\frac{a_n}{n}=\)____。
[選填題]設 \( A(6n, 0) \)、\( B(0, 3) \),直線 \( AB \) 的方程為 \( y = -\frac{1}{2n}x + 3 \),\( T_n \) 是 \( \triangle OAB \) 內部(含邊界)的區域。
統計 \( T_n \) 內整數點的個數 \( a_n \):
- 當 \( y=0 \) 時,\( x \) 可取 \( 0 \sim 6n \),共 \( 6n+1 \) 個點;
- 當 \( y=1 \) 時,代入直線方程得 \( x \leq 4n \),故 \( x \) 可取 \( 0 \sim 4n \),共 \( 4n+1 \) 個點;
- 當 \( y=2 \) 時,代入得 \( x \leq 2n \),故 \( x \) 可取 \( 0 \sim 2n \),共 \( 2n+1 \) 個點;
- 當 \( y=3 \) 時,僅有 \( (0, 3) \),共 \( 1 \) 個點。
因此:
\[
a_n = (6n+1) + (4n+1) + (2n+1) + 1 = 12n + 4
\]
求極限:
\[
\lim_{n \to \infty} \frac{a_n}{n} = \lim_{n \to \infty} \frac{12n + 4}{n} = 12
\]