〈動能計算〉彙整頁面

110指考物理分科考科_07

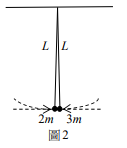
有兩顆大小相同的小球，各以長度為L、質量可忽略不計的擺錘掛在天花板同一點，左邊小球的質量為 \( 2m \)，右邊小球的質量為 \( 3m \)。某生拉起兩小球至高度分別為 \( h_L \) 和 \( h_R \)，將小球由靜止釋放，讓小球擺向中間，使兩小球恰在最低點時發生正向彈性碰撞，如圖2所示。碰撞後，若左邊的小球擺回到最高點的高度仍然為 \( h_L \)，則 \( h_L : h_R \) 為何？
(A)9:4
(B)3:2
(C)1:1
(D)2:3
(E)4:9

[單選題]

答案

略解：碰撞前速率：\( v_{2m} = \sqrt{2gh_L} \)，\( v_{3m} = -\sqrt{2gh_R} \)（設向右為正）。
彈性碰撞後，左球速度：
\( v_{2m}' = \frac{2m-3m}{2m+3m} \sqrt{2gh_L} + \frac{2 \times 3m}{2m+3m} (-\sqrt{2gh_R}) = -\frac{1}{5} \sqrt{2gh_L} - \frac{6}{5} \sqrt{2gh_R} \)。
題意 \( v_{2m}' = -\sqrt{2gh_L} \)，故 \( -\sqrt{h_L} = -\frac{1}{5} \sqrt{h_L} - \frac{6}{5} \sqrt{h_R} \Rightarrow \frac{4}{5} \sqrt{h_L} = \frac{6}{5} \sqrt{h_R} \Rightarrow \sqrt{h_L} : \sqrt{h_R} = 3:2 \Rightarrow h_L : h_R = 9:4 \)。
答案：A

加最愛

110指考物理分科考科_25

一、在「金屬的比熱」實驗單元中，有相同質量的兩個純金屬塊A和B，其上的標籤都已脫落在旁，標籤一：比熱0.39J/(g°C)，標籤二：比熱0.15J/(g°C)，因而進行實驗探討，以測定金屬塊的比熱，並貼上正確標籤。已知水的比熱為4.2J/(g°C)，量熱器質量為600g。經多次實驗平均後，得到的數據取兩位有效數字節錄如表1與表2。表1為熱水加到盛有冷水的量熱器過程中所得到的實驗數據。表2為將金屬塊A投入盛有冷水的量熱器過程中所得到的實驗數據。冷水的初始溫度為冷水加入量熱器內達到熱平衡後的溫度。

表1	質量(g)	初始溫度(°C)	熱平衡溫度(°C)
熱水	200	100	65
冷水	100	15	65

表2	質量(g)	初始溫度(°C)	熱平衡溫度(°C)
冷水	100	19	24
金屬塊A	100	100	24

1. 進行表1的測量時，先將冷水加入量熱器達到熱平衡後再加入熱水，而不是直接將熱水加入量熱器，說明此實驗步驟的目的為何？（2分）
2. 實驗時，金屬塊的體積相對於量熱器中的體積有哪些限制？簡單說明理由。（2分）
3. 根據實驗數據，計算金屬塊A的比熱（至兩位有效數字）。（3分）
4. 若另以電熱板對金屬塊B直接加熱，進行比熱測量實驗，實驗時以0.50A的電流、12V的電壓對金屬塊B加熱2.0分鐘，測得的實驗數據如表3，試判定金屬塊B的比熱，並計算電熱板提供的熱量被金屬塊B吸收的百分比。（3分）

表3	質量(g)	初始溫度(°C)	最終溫度(°C)
金屬塊B	100	22	58

[非選擇題]

答案

略解：1. 使量熱器與冷水先達熱平衡，可減少後續實驗中量熱器吸熱造成的誤差，並使系統初溫接近室溫，減少熱散失。
2. 金屬塊體積需小於水量，使其能完全沒入水中，確保熱交換完全。體積也不宜過大，避免水量相對過少導致溫度變化太大，增加誤差。
3. 由表1求量熱器比熱 \( s_c \)：
吸熱：量熱器 \( 600 \times s_c \times (65-15) \)，冷水 \( 100 \times 4.2 \times (65-15) \)。
放熱：熱水 \( 200 \times 4.2 \times (100-65) \)。
能量守恆：\( 600 s_c \times 50 + 100 \times 4.2 \times 50 = 200 \times 4.2 \times 35 \)
\( 30000 s_c + 21000 = 29400 \Rightarrow 30000 s_c = 8400 \Rightarrow s_c = 0.28 \text{J/g°C} \)。
由表2求 \( s_A \)：
吸熱：量熱器 \( 600 \times 0.28 \times (24-19) \)，冷水 \( 100 \times 4.2 \times (24-19) \)。
放熱：金屬A \( 100 \times s_A \times (100-24) \)。
\( 600 \times 0.28 \times 5 + 100 \times 4.2 \times 5 = 100 \times s_A \times 76 \)
\( 840 + 2100 = 7600 s_A \Rightarrow 2940 = 7600 s_A \Rightarrow s_A \approx 0.39 \text{J/g°C} \)。
4. 電能 \( E_{\text{電}} = IVt = 0.50 \times 12 \times (2.0 \times 60) = 720 \text{J} \)。
金屬B吸熱 \( Q_B = 100 \times s_B \times (58-22) = 3600 s_B \)。
由標籤知 \( s_B = 0.15 \text{J/g°C} \)，故 \( Q_B = 3600 \times 0.15 = 540 \text{J} \)。
吸收百分比 \( = \frac{540}{720} \times 100\% = 75\% \)。
答案：1. 減少熱損失誤差 2. 體積需小於水量，確保完全沒入 3. \( 0.39 \text{J/g°C} \) 4. \( 0.15 \text{J/g°C} \)，75%

加最愛

111物理分科測驗–02

如圖1所示，質量m的甲球自高度H處，由靜止開始沿光滑軌道下滑至水平部分後，與質量亦為m的靜止乙球發生總動能守恆的一維碰撞。已知重力加速度為g，且取水平向右為正值速度的方向，則兩球碰撞後，甲球的速度v_1與乙球的速度v_2為下列何者？
(A) \( v_1 = v_2 = \frac{1}{2} \sqrt{2gH} \)
(B) \( v_1 = -v_2 = -\frac{1}{2} \sqrt{2gH} \)
(C) \( v_1 = -v_2 = \sqrt{gH} \)
(D) \( v_1 = 0, v_2 = \sqrt{2gH} \)
(E) \( v_1 = 0, v_2 = \sqrt{gH} \)

[單選題]

答案

甲球下滑過程力學能守恆得碰撞前速度 \( v_0 = \sqrt{2gH} \)。質量相等物體彈性碰撞速度交換，故 \( v_1 = 0, v_2 = \sqrt{2gH} \)，選(D)。

加最愛

111物理分科測驗–04

進行焦耳實驗時，使兩個質量各為0.42kg的重錘落下1.0m，以帶動葉片旋轉，攪動容器內2.0L的水。已知水的比熱為4.2kJ/(kg·K)，水所散失的熱量可忽略，重力加速度 \( g = 10 m/s^2 \)，則攪動後水溫上升約為何？
(A) 0.0010K
(B) 0.010K
(C) 0.10K
(D) 1.0K
(E) 10K

[單選題]

答案

重錘位能損失 \( W = 2mgh = 2 \times 0.42 \times 10 \times 1 = 8.4 \) J。水吸收熱能 \( H = mc\Delta T = 2.0 \times 4.2 \times 10^3 \times \Delta T \)。由 \( W = H \) 得 \( 8.4 = 8400 \Delta T \)，故 \( \Delta T = 0.001 \) K，選(A)。

加最愛

111物理分科測驗–17

依據波耳的氫原子模型，若兩個處於量子數 \( n = 1 \) 的基態氫原子，在發生正向碰撞後停止不動，接著都只發出同一種單頻光。其光子的能量均為 10.204eV，則下列敘述哪些正確？ (氫原子的質量為 \( 1.67 \times 10^{-27} kg \)，氫原子的能量為 \( E_n = -13.606eV/n^2 \)，\( 1eV = 1.602 \times 10^{-19} J \) )
(A) 碰撞後兩個氫原子都被激發到 \( n = 2 \) 的能階
(B) 在碰撞前每個氫原子的動能都為 3.4eV
(C) 在碰撞前兩個氫原子的總動量大於零
(D) 在碰撞前每個氫原子的速率大於 30 km/s
(E) 兩個氫原子發出的都是可見光

[多選題]

答案

光子能量 10.204 eV 對應躍遷 \( \Delta E = E_2 - E_1 = -13.606/4 - (-13.606) = 10.204 \) eV，故碰撞後激發至 n=2，(A)對。碰撞後靜止，動能轉為激發能，故碰撞前總動能 20.408 eV，每個原子動能 10.204 eV，(B)錯。碰撞前後總動量為0，(C)錯。由 \( K = \frac{1}{2}mv^2 \) 得 \( v \approx 4 \times 10^4 \) m/s = 40 km/s > 30 km/s，(D)對。光子波長 \( \lambda = \frac{hc}{E} \approx 121.5 \) nm，紫外光，(E)錯。選(A)(D)。

加最愛

112物理分科測驗–08

[題組:第8題到第9題] ◎一質量為 \( m \) 的小木塊，前方繫有一理想彈簧，如圖 2 所示。此系統由光滑斜面頂端自靜止滑下，進入光滑水平面後正向撞上鉛直牆面，彈簧因被壓縮而使木塊減速，並將木塊原本的動能轉換為彈簧位能，之後木塊在某一瞬間停止不動，定義此為終點。木塊自初始靜止至終點的整個過程，木塊下降的鉛直高度為 \( h \)，令重力加速度為 \( g \)，且過程中力學能守恆、系統到達最大速率前尚未撞上牆面，回答下列問題。
下列敘述何者正確？
(A)木塊所達到的最大動能為 \( mgh \)
(B)整個過程中，彈簧對木塊所作的功為正值，且等於 \( mgh \)
(C)彈簧的彈性位能在終點時比在初始靜止時增加 \( \frac{mgh}{2} \)
(D)木塊在終點的瞬間，彈簧對牆面的水平作用力量值必小於 \( mg \)
(E)彈簧被壓縮的過程中，木塊進行等加速運動

[題組題]

答案

全程力學能守恆，初位能 \( mgh \) 轉為動能與彈簧位能。(A)對：最大動能發生在斜面底端未撞牆時，為 \( mgh \)。(B)錯：彈簧對木塊作負功。(C)錯：終點彈簧位能為 \( mgh \)，增加 \( mgh \)。(D)錯：彈力與 \( mg \) 無直接關係。(E)錯：彈簧壓縮為變加速度運動。選(A)。

加最愛

112物理分科測驗–16

有一環繞地球、原本保持圓周運動的人造衛星，因故失去可微調軌道使保持固定速率的動力，現受空氣阻力影響造成其離地高度逐漸變小。假設人造衛星的質量始終不變，在其失去動力後，下列敘述哪些正確？
(A)動量值始終不變
(B)角動量值逐漸變小
(C)總力學能逐漸變小
(D)重力位能逐漸變大
(E)重力位能逐漸變小

[多選題]

答案

高度變小，軌道半徑 \( r \) 變小。(A)錯：\( v = \sqrt{\frac{GM}{r}} \)，r變小v變大，動量 \( p = mv \) 變大。(B)對：\( L = m v r = m\sqrt{GMr} \)，r變小L變小。(C)對：空氣阻力作負功，總力學能減少。(D)錯(E)對：重力位能 \( U = -\frac{GMm}{r} \)，r變小，U變小（負值變大）。選(B)(C)(E)。

加最愛

113物理分科測驗05

在入射光的頻率高於底限頻率（截止頻率）的光電效應實驗中，實驗測得的截止電壓（遏止電位）與下列何者成正比？
(A)電子在被激發出之前的能量
(B)入射光的強度
(C)光電流的強度
(D)被照射金屬靶的功因數
(E)光電子的最大動能

[單選題]

答案

光電效應方程式：\(h\nu = W + K_{\text{max}}\)，其中 \(K_{\text{max}} = eV_c\)，故截止電壓 \(V_c\) 與光電子最大動能 \(K_{\text{max}}\) 成正比。故選(E)。答案：E

加最愛

113物理分科測驗16

在新款車的碰撞安全測試中，一輛質量為 2000kg 的汽車，以等速度 72km/h（20m/s）在水平地面上直線前進，和質量為 1000kg 的靜止箱形障礙物發生一維非彈性正向碰撞。碰撞後箱形障礙物被向前彈開，汽車車頭內凹但仍持續向前行進。假設空氣阻力與地面摩擦力可忽略。在此碰撞過程中，速度感測器測得碰撞開始後汽車速率與時間的關係如圖 6 所示。將開始碰撞的時間記為 0.0 秒，則下列敘述哪些正確？
(A)在 0.5 秒後，汽車與障礙物分離
(B)在 0.5 秒後，汽車動能減少一半
(C)在 0.5 秒後，障礙物速率為 20m/s
(D)在 0.5 秒內，汽車平均加速度量值為 10m/s\(^2\)
(E)在 0.5 秒後，汽車與障礙物的總動能減少 \(1 \times 10^5\) J

[多選題]

答案

由圖，0.5s後汽車速率为10m/s不再變，故(A)對。
動量守恆：\(2000\times20 = 2000\times10 + 1000\times v\)，得 \(v=20 \text{m/s}\)，故(C)對。
汽車動能減少：\(\frac{1}{2}\times2000\times(20^2-10^2)=300000 \text{J}\)，非一半，(B)錯。
加速度 \(a = \frac{10-20}{0.5} = -20 \text{m/s}^2\)，(D)錯。
總動能減少：\(\frac{1}{2}\times2000\times20^2 - (\frac{1}{2}\times2000\times10^2 + \frac{1}{2}\times1000\times20^2) = 100000 \text{J}\)，(E)對。故選(A)(C)(E)。答案：ACE

加最愛

113物理分科測驗19

[題組：第19–20題]

◎ 風能為再生能源，可作為實現淨零碳排的綠色能源。風力發電（簡稱：風電）利用風力帶動風電葉片旋轉，將風的動能透過發電模組轉換成電能，其功率 \( P \) 與單位時間內空氣流向風電葉片的氣流動能成正比。

19. 空氣以速度 \( v \) 垂直流向風電葉片，葉片旋轉所形成的假想圓形平面其面積為 \( A \)，如圖8。

(a) 在時間 \( \Delta t \) 內，密度為 \( \rho \) 的空氣流向風電葉片的質量 \( m \) 為何？（請以試題中所定義的參數符號表示）（2分）

(b) 風電的功率 \( P \) 與風速的三次方（\( v^3 \)）成正比，請說明其原因為何？（3分）

[題組題]

答案

(a) \(m = \rho A v \Delta t\)
(b) 單位時間動能 \(\frac{E_k}{\Delta t} \propto \frac{1}{2} m v^2\)，代入 \(m \propto v\)，得 \(P \propto v^3\)。答案：(a) \(m = \rho A v \Delta t\) (b) 略解如上

加最愛

Saved articles