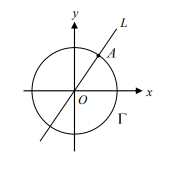
如右圖，\( L \) 為坐標平面上通過原點 \( O \) 的直線，\( \Gamma \) 是以 \( O \) 為圓心的圓，且 \( L \) 與 \( \Gamma \) 有一個交點 \( A(3, 4) \)。已知 \( B \cdot C \) 為 \( \Gamma \) 上的相異兩點滿足 \( BC = OA \)。試選出正確的選項。
(1) \( L \) 與 \( \Gamma \) 的另一個交點為 \( (-4, -3) \)
(2) 直線 \( BC \) 的斜率為 \(\frac{3}{4}\)
(3) ∠\( AOC = 60^\circ\)
(4) △\( ABC \) 的面積為 \(\frac{25\sqrt{3}}{2}\)
(5) \( B \) 與 \( C \) 在同一象限內
在 \(\triangle ABC\) 中，已經知道 \(AB = 4\) 和 \(AC = 6\)，此時尚不足以確定 \(\triangle ABC\) 的形狀與大小。但是，只要再知道某些條件（例如：再知道 \(BC\) 的長度），就可確定 \(\triangle ABC\) 唯一的形狀與大小。試選出正確的選項。
(1) 如果再知道 \(\cos A\) 的值，就可確定 \(\triangle ABC\) 唯一的形狀與大小
(2) 如果再知道 \(\cos B\) 的值，就可確定 \(\triangle ABC\) 唯一的形狀與大小
(3) 如果再知道 \(\cos C\) 的值，就可確定 \(\triangle ABC\) 唯一的形狀與大小
(4) 如果再知道 \(\triangle ABC\) 的面積，就可確定 \(\triangle ABC\) 唯一的形狀與大小
(5) 如果再知道 \(\triangle ABC\) 的外接圓半徑，就可確定 \(\triangle ABC\) 唯一的形狀與大小
如右圖，機器人在地面上從一點 \(P\) 出發，按照以下規則移動：先朝某方向前進一公尺後，依前進方向逆時針旋轉 \(45^\circ\)；朝新方向前進一公尺後，依前進方向順時針旋轉 \(90^\circ\)；再朝新方向前進一公尺後，依前進方向逆時針旋轉 \(45^\circ\)；再朝新方向前進一公尺後，依前進方向順時針旋轉 \(90^\circ\) ……，以此類推。已知機器人移動的路徑會形成一個封閉區域，則此封閉區域的面積為 \(\underline{\qquad\qquad} + \underline{\qquad\qquad} \sqrt{\qquad\qquad}\) 平方公尺。（化成最簡根式）
在四面體 \(ABCD\) 中，\(\overline{AB} = AC = AD = 4\sqrt{6} \cdot BD = CD = 8\)，且 \(\cos \angle BAC = \frac{1}{3}\)，則點 \(D\) 到平面 \(ABC\) 的距離為 \(\underline{\qquad\qquad}\)。（化成最簡根式）
坐標平面上，\( \triangle ABC \) 三頂點的坐標分別為 \( A(0, 2), B(1, 0), C(4, 1) \)，試選出正確的選項。
(1) \( \triangle ABC \) 的三邊中，\( \overline{AC} \) 最長
(2) \( \sin A \lt \sin C \)
(3) \( \triangle ABC \) 為銳角三角形
(4) \( \sin B = \frac{7\sqrt{2}}{10} \)
(5) \( \triangle ABC \) 的外接圓半徑比2小
[題組:第18-20題]坐標平面上有一環狀區域由圓 \( x^2+y^2=3 \) 的外部與圓 \( x^2+y^2=4 \) 的內部交集而成。某甲欲用一支長度為1的筆直掃描棒來掃描此環狀區域之x軸上方的某區域R。他設計掃描棒黑、白兩端分別在半圓 \( C_1: x^2+y^2=3 \) (\( y \geq 0 \))、\( C_2: x^2+y^2=4 \) (\( y \geq 0 \))上移動。開始時掃描棒黑端在點 \( A(\sqrt{3}, 0) \)，白端在 \( C_2 \) 的點 \( B \)。接著黑、白兩端各沿著 \( C_1 \)、\( C_2 \) 逆時針移動，直至白端碰到 \( C_2 \) 的點 \( B'(-2, 0) \)便停止掃描。
18. 試問點 \( B \) 的坐標為下列哪一選項？（單選題，3分）
(1) \( (0, 2) \)
(2) \( (1, \sqrt{3}) \)
(3) \( (\sqrt{2}, \sqrt{2}) \)
(4) \( (\sqrt{3}, 1) \)
(5) \( (2, 0) \)
坐標平面上，\( P(a, 0) \) 為 x 軸上一點，其中 \( a \gt 0 \)。令 \( L_1 \)、\( L_2 \) 為通過 \( P \) 點，斜率分別為 \( -\frac{4}{3} \)、\( -\frac{3}{2} \) 的直線。已知 \( L_1 \)、\( L_2 \) 分別與兩坐標軸圍成的兩個直角三角形的面積差為 3，試問 \( a \) 值為何？
(1) \( 3\sqrt{2} \) (2) 6 (3) \( 6\sqrt{2} \) (4) 9 (5) \( 8\sqrt{2} \)
坐標空間中有三個彼此互相垂直之向量 \(\overset{\rightharpoonup}{u}\)、\(\overset{\rightharpoonup}{v}\)、\(\overset{\rightharpoonup}{w}\)。已知 \(\overset{\rightharpoonup}{u}-\overset{\rightharpoonup}{v}=(2,-1,0)\)，且 \(\overset{\rightharpoonup}{v}-\overset{\rightharpoonup}{w}=(-1,2,3)\)。試問由 \(\overset{\rightharpoonup}{u}\)、\(\overset{\rightharpoonup}{v}\)、\(\overset{\rightharpoonup}{w}\) 所張出的平行六面體之體積為何？
(1) \(2\sqrt{5}\) (2) \(5\sqrt{2}\) (3) \(2\sqrt{10}\) (4) \(4\sqrt{5}\) (5) \(4\sqrt{10}\)
由三向量垂直，體積為 \(|\overset{\rightharpoonup}{u}||\overset{\rightharpoonup}{v}||\overset{\rightharpoonup}{w}|\)。
設 \(|\overset{\rightharpoonup}{u}|^2+|\overset{\rightharpoonup}{v}|^2+|\overset{\rightharpoonup}{w}|^2=15\)，且由已知向量差求得各向量長平方：\(|\overset{\rightharpoonup}{u}|^2=1\)，\(|\overset{\rightharpoonup}{v}|^2=4\)，\(|\overset{\rightharpoonup}{w}|^2=10\)。
體積 \(=\sqrt{1\cdot4\cdot10}=2\sqrt{10}\)，故選(3)。 報錯
ChatGPT DeepSeek
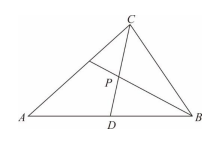在 \(\triangle ABC\) 中，\(\overline{AB} = 6\)，\(\overline{AC} = 5\)，\(\overline{BC} = 4\)。令 \(\overline{AB}\) 中點為 \(D\)，\(P\) 為 \(\angle ABC\) 之角平分線與 \(\overline{CD}\) 之交點，如右圖所示。試選出正確的選項。
(1) \(\overline{CP} = \frac{3}{7}\overline{CD}\)
(2) \(\overset{\rightharpoonup}{AP} = \frac{3}{7}\overset{\rightharpoonup}{AB} + \frac{2}{7}\overset{\rightharpoonup}{AC}\)
(3) \(\cos \angle BAC = \frac{3}{4}\)
(4) \(\triangle ACP\) 面積為 \(\frac{15}{14}\sqrt{7}\)
(5) (內積) \(\overset{\rightharpoonup}{AP} \cdot \overset{\rightharpoonup}{AC} = \frac{120}{7}\)
(1) ✗：\(\overline{CP}=\frac{4}{7}\overline{CD}\)；(2) ✗：\(\overset{\rightharpoonup}{AP}=\frac{2}{7}\overset{\rightharpoonup}{AB}+\frac{3}{7}\overset{\rightharpoonup}{AC}\)；
(3) ✓：餘弦定理得 \(\cos \angle BAC=\frac{3}{4}\)；(4) ✓：面積計算得 \(\frac{15\sqrt{7}}{14}\)；
(5) ✓：內積計算得 \(\frac{120}{7}\)。
故選(3)(4)(5)。 報錯
ChatGPT DeepSeek
已知實係數三次多項式 \(f(x)\) 除以 \(x+6\) 得商式 \(q(x)\) 和餘式 3。若 \(q(x)\) 在 \(x=-6\) 有最大值 8，則 \(y=f(x)\) 圖形的對稱中心坐標為 \((\)__________\(,\)__________\()\)。
