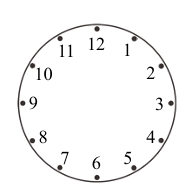
一個標有1至12號格子的12格戳戳樂遊戲,每回遊戲以投擲一枚均勻銅板四次來決定要戳哪些格子。規則如下:
(一)第一次投擲銅板,若是正面,則戳1號格子;若是反面,則戳3號格子。
(二)第二、三、四次投擲銅板,若是正面,則所戳格子的號碼為前一次所戳格子的號碼加1;若是反面,則所戳格子的號碼為前一次所戳格子的號碼加3,依此類推。
例如:投擲銅板四次的結果依序為「正、反、反、正」,則會戳編號分別為1、4、7、8號的四個格子。
假設\(p_{m}\)代表在每回遊戲中\(m\)號格子被戳到的機率,試選出正確的選項。
(1)\(p_{2}=\frac{1}{4}\)
(2)\(p_{3}=\frac{1}{2}\)
(3)\(p_{4}=\frac{1}{2}p_{1}+\frac{1}{2}p_{3}\)
(4)\(p_{8}>p_{10}\)
(5)在4號格子被戳到的條件下,3號格子被戳到的機率為\(\frac{1}{2}\)
(1)要戳到2號格子,第一次需正面(概率\(\frac{1}{2}\))且第二次正面(概率\(\frac{1}{2}\)),所以\(p_{2}=\frac{1}{2}\times\frac{1}{2}=\frac{1}{4}\) ,(1)正確。
(2)第一次投擲正面戳1號格,第二次反面可戳到3號格;第一次投擲反面戳3號格,所以\(p_{3}=\frac{1}{2}\times\frac{1}{2}+\frac{1}{2}=\frac{3}{4}\) ,(2)錯誤。
(3)若第一次戳1號格(概率\(\frac{1}{2}\)),第二次正面可到4號格;若第一次戳3號格(概率\(\frac{1}{2}\)),第二次正面也可到4號格,所以\(p_{4}=\frac{1}{2}p_{1}+\frac{1}{2}p_{3}\) ,(3)正正確。
(4)計算可得\(p_{8}=\frac{1}{4}\) ,\(p_{10}=\frac{1}{8}\) ,所以\(p_{8}>p_{10}\) ,(4)正確。
(5)(5)×:\(P(\text{擊中3號} \mid \text{擊中4號}) = \dfrac{P(\text{擊中3號且擊中4號})}{P(\text{擊中4號})} = \dfrac{\left( \dfrac{1}{2} \right)^4 + \left( \dfrac{1}{2} \right)^2}{\dfrac{9}{16}} = \dfrac{5}{9}\),(5)錯誤。答案為(1)(3)(4)。