設 \(a, b, c\) 均為正整數，且 \(1\lt a\lt b\lt c\lt 9\)，若 \(\frac{a}{5}\)，\(\frac{b}{10}\)，\(\frac{c}{15}\) 三數成等比，則公比為何？
\((1) 2\)
\((2) 1\)
\((3) 0.5\)
\((4) 0.25\)
\((5) 0.125\)
等比數列中項性質：\((\frac{b}{10})^2 = \frac{a}{5} \times \frac{c}{15}\)，化簡得 \(3b^2 = 2ac\)。代入正整數 \(a=2\)、\(b=4\)、\(c=6\)（滿足 \(1\lt a\lt b\lt c\lt9\)），公比 \(r = \frac{\frac{4}{10}}{\frac{2}{5}} = 1\)。答案：\((2)\)
設 \(\triangle ABC\) 中，\(\angle A\)、\(\angle B\)、\(\angle C\) 的對邊邊長分別為 \(a\)、\(b\)、\(c\)，已知 \(b^2 = ac\)，若點 \(D\) 在 \(\overline{AC}\) 邊上，且 \(\overline{BD} = \overline{AC}\)，\(\overline{AD} = 3\overline{CD}\)，試求 $\cos\angle ABC = \frac{~~~~~~~~~~~}{~~~~~~~~~~}$（化為最簡分數）
[選填題]設 \(CD = x\)，則 \(AD = 3x\)，\(AC = b = 4x\)，\(BD = b = 4x\)。在 \(\triangle BCD\) 與 \(\triangle ABC\) 用餘弦定理，聯立 \(b^2 = ac\)，得 \(12a^2 - 19ac + 4c^2 = 0\)，解得 \(a = \frac{4c}{3}\)。代入 \(\cos\angle ABC = \frac{a^2 + c^2 - b^2}{2ac}\)，得 \(\frac{13}{24}\)。答案：\(\frac{13}{24}\)
坐標平面中 \(A(a, 3)\)、\(B(16, b)\)、\(C(19, 12)\) 三點共線。已知 \(C\) 不在 \(A, B\) 之間,且 \(AC : BC = 3 : 1\),則 \(a + b =\)__________。
[選填]已知某校老師玩過「寶可夢」的比率為 \( r_1 \)，而學生玩過的比率為 \( r_2 \)，其中 \( r_1 \neq r_2 \)。由下列選項中的資訊，請選出可以判定全校師生玩過「寶可夢」的比率之選項：
(1)全校老師與學生比率
(2)全校老師人數
(3)全校學生人數
(4)全校師生人數
(5)全校師生玩過「寶可夢」人數。
在坐標平面上，△ABC 內有一點 P 滿足 \(\overrightarrow{AP} = \left( \frac{4}{3}, \frac{5}{6} \right)\) 及 \(\overrightarrow{AP} = \frac{1}{2} \overrightarrow{AB} + \frac{1}{5} \overrightarrow{AC}\)。若 A, P 連線交 BC 於 M，則 \(\overrightarrow{AM} = \left( \underline{\qquad}, \underline{\qquad} \right)\)。（化成最簡分數）
[選填題]設\(\overrightarrow{AM} = t \overrightarrow{AP} = t\left( \frac{1}{2} \overrightarrow{AB} + \frac{1}{5} \overrightarrow{AC} \right) = \frac{t}{2} \overrightarrow{AB} + \frac{t}{5} \overrightarrow{AC}\)。
因M在BC上，故係數和為1：\(\frac{t}{2} + \frac{t}{5} = 1 \Rightarrow \frac{7t}{10} = 1 \Rightarrow t = \frac{10}{7}\)。
故\(\overrightarrow{AM} = \frac{10}{7} \overrightarrow{AP} = \frac{10}{7} \left( \frac{4}{3}, \frac{5}{6} \right) = \left( \frac{40}{21}, \frac{25}{21} \right)\)。答案：\(\left( \frac{40}{21}, \frac{25}{21} \right)\)
設 \( a, b, x \) 皆為正整數且滿足 \( a \leq x \leq b \) 及 \( b-a=3 \)。若用內插法從 \(\log a, \log b \) 求得 \(\log x \) 的近似值為 \(\log x \approx \frac{1}{3} \log a + \frac{2}{3} \log b = \frac{1}{3} (1 + 2 \log 3 – \log 2) + \frac{2}{3} (4 \log 2 + \log 3)\)，則 \( x \) 的值為 \(\underline{\qquad}\)。
[選填題]計算右式：
\(\frac{1}{3}(1 + 2\log 3 - \log 2) + \frac{2}{3}(4\log 2 + \log 3) = \frac{1}{3} + \frac{2}{3}\log 3 - \frac{1}{3}\log 2 + \frac{8}{3}\log 2 + \frac{2}{3}\log 3\)
\(= \frac{1}{3} + \frac{4}{3}\log 3 + \frac{7}{3}\log 2 = \frac{1}{3} + \log(3^{4/3} \cdot 2^{7/3})\)。
近似計算：\(\frac{1}{3}(1 + 2\log 3 - \log 2) \approx \frac{1}{3}(1 + 0.9542 - 0.3010) = \frac{1}{3}(1.6532) \approx 0.5511\)，對應數值約為 \(10^{0.5511} \approx 3.56\)，此為\(\log a\)？需重新審視。
原解析直接計算：
\(\frac{1}{3}(1 + 2\log 3 - \log 2) = \frac{1}{3}(\log 10 + \log 9 - \log 2) = \frac{1}{3}\log\left(\frac{10 \times 9}{2}\right) = \frac{1}{3}\log 45\)。
\(\frac{2}{3}(4\log 2 + \log 3) = \frac{2}{3}(\log 16 + \log 3) = \frac{2}{3}\log 48\)。
故\(\log x \approx \frac{1}{3}\log 45 + \frac{2}{3}\log 48\)。由內插法，x位於45與48之間，且距離比為1:2，故\(x = \frac{1 \times 45 + 2 \times 48}{1+2} = \frac{141}{3} = 47\)。答案：47
某貨品為避免因成本變動而造成售價波動太過劇烈，當週售價相對於前一週售價的漲跌幅定為當週成本相對於前一週成本的漲跌幅的一半。例如下表中第二週成本上漲100%，所以第二週售價上漲50%。依此定價方式以及下表的資訊，試選出正確的選項。
(1) \(120 = x \lt y \lt 180\)
(2) \(120 \lt x \lt y \lt 180\)
(3) \(x \lt 120 \lt y \lt 180\)
(4) \(120 = x \lt 180 \lt y\)
(5) \(120 \lt x \lt 180 \lt y\)。
某地區衛生機構成功訪問了500人，其中年齡為50-59歲及60歲（含）以上者分別有220名及280名。這500名受訪者中，120名曾做過大腸癌篩檢，其中有75名是在一年之前做的，有45名是在一年之內做的。已知受訪者中，60歲（含）以上者曾做過大腸癌篩檢比率是50-59歲者曾做過大腸癌篩檢比率的3.5倍，試選出正確的選項。
(1)受訪者中年齡為60歲（含）以上者超過60%
(2)由受訪者中隨機抽取兩人，此兩人的年齡皆落在50-59歲間的機率大於0.25
(3)由曾做過大腸癌篩檢的受訪者中隨機抽取兩人，其中一人在一年之內受檢而另一人在一年之前受檢的機率為\(2\cdot\frac{45}{120} \times \frac{75}{119}\)
(4)這500名受訪者中，未曾做過大腸癌篩檢的比率低於75%
(5)受訪者中60歲（含）以上者，曾做過大腸癌篩檢的人數超過90名。
(1) \(280/500=56\% \lt 60\%\)。
(2) 機率為\(C^{220}_2 / C^{500}_2 \approx (220/500)^2 \lt 0.25\)。
(3) 正確，抽兩人一為一年內、一為一年前，機率為\(\frac{C^1_{45} C^1_{75}}{C^2_{120}} = \frac{45 \times 75}{120 \times 119}\)。
(4) 未曾篩檢比率為\((500-120)/500=76\% \gt 75\%\)。
(5) 設60歲以上篩檢x人，則\(x/280 = 3.5 \times (120-x)/220\)，解得\(x=98 \gt 90\)。
故選(3)(5)。答案：(3)(5)
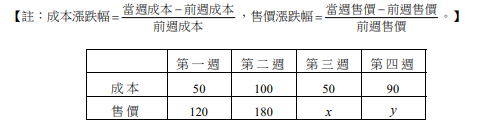
下表是2011年至2018年某國總就業人口與農業就業人口的部分相關數據，各年度的人口以人數計，有些是以千人計，有些以萬人計，例如2011年總就業人口為1,070.9萬人，65歲以上男性農業就業人口為69.1千人。試根據表格資料選出正確的選項。
| 年份 | 總就業人口（萬人） | 農業就業人口（萬人） | 男性農業就業人口（千人） | 39歲以下（千人） | 40-49歲（千人） | 50-64歲（千人） | 65歲以上（千人） |
|---|---|---|---|---|---|---|---|
| 2011年 | 1,070.9 | 54.2 | 386.3 | 67.6 | 85.4 | 164.2 | 69.1 |
| 2012年 | 1,086.0 | 54.4 | 394.9 | 67.5 | 87.0 | 169.5 | 70.9 |
| 2013年 | 1,096.7 | 54.4 | 391.5 | 66.6 | 83.9 | 171.3 | 69.7 |
| 2014年 | 1,107.9 | 54.8 | 391.2 | 65.8 | 79.8 | 173.0 | 72.6 |
| 2015年 | 1,119.8 | 55.5 | 403.1 | 71.7 | 76.9 | 181.3 | 73.2 |
| 2016年 | 1,126.7 | 55.7 | 404.5 | 77.4 | 77.4 | 176.4 | 73.3 |
| 2017年 | 1,135.2 | 55.7 | 405.1 | 73.9 | 78.1 | 178.3 | 74.8 |
| 2018年 | 1,143.4 | 56.1 | 415.1 | 72.0 | 78.8 | 184.9 | 79.4 |
(1)從2013年至2018年，65歲以上的男性農業就業人口逐年遞增
(2)從2013年至2018年，50歲至64歲之男性農業就業人口逐年遞增
(3)上表中，每一年的男性農業就業人口占總就業人口的比率都小於百分之五
(4)上表中，每一年50歲至64歲之男性農業就業人口都少於49歲以下之男性農業就業人口
(5)就65歲以上之男性農業就業人口而言，2018年比2011年增加了不到一萬人。
某村的村長選舉設有兩個投票所。已知兩位候選人在各投票所得的有效票數比例如下表（廢票不列入計算）：
| 甲候選人 | 乙候選人 | |
| 第一投票所 | 40 % | 60 % |
| 第二投票所 | 55 % | 45 % |
假設第一投票所與第二投票所的有效票數分別為 \( x \) 與 \( y \)（其中 \( x > 0, y > 0 \)），且以總得票數較高者為當選人。根據上述表格，試選出正確的選項。
(1) 當有效票數的總和 \( x + y \) 已知時，就可決定當選人
(2) 當 \( x : y \) 的比值小於 \(\frac{1}{2}\) 時，就可決定當選人
(3) 當 \( x > y \) 時，就可決定當選人
(4) 當甲候選人在第一投票所的有效票數比在第二投票所的有效票數多時，就可決定當選人
(5) 當乙候選人在第二投票所的有效票數比在第一投票所的有效票數多時，就可決定當選人
