比例
113學測數學A考科_13
某銷售站銷售甲、乙、丙三型手機，甲手機每支利潤 100 元，乙手機每支利潤 400 元，丙手機每支利潤 240 元。上年度甲、乙、丙手機各賣出 A，B，C 支，平均每支利潤為 260 元；且知銷售甲、乙兩型手機共 A＋B 支的平均每支利潤為 280 元。則該站上年度售出的三型手機數量比為 A：B：C＝ __________：__________：__________。(化為最簡整數比)
[選填題]
答案
107指考數學乙試題-07
保險公司把投保額盜險的住宅分為 \( A \)、\( B \) 兩級，其所占比率分別為60%、40%。過去一年 \( A \)、\( B \) 兩級住宅遭竊的比率分別為15%、5%。據此，公司推估未來一年 \( A \)、\( B \) 兩級住宅被竊的機率分別為0.15、0.05。今A級住宅中的20%經過改善，重新推估這些改善過的住宅未來一年被竊的機率會降為0.03；而其他住宅被竊機率不變。根據以上資料，試選出正確的選項。
(1) 全體投保的住宅中，過去一年遭竊的比率為12%
(2) 過去一年遭竊的投保住宅中，A級所占的比率超過90%
(3) 推估未來一年，改善過的A級住宅的被竊機率為原來的 \(\frac{1}{5}\)
(4) 經改善後，推估未來一年被竊機率，全體投保的A級住宅會小於全體投保的B級住宅
(5) 經改善後，推估未來一年全體投保的住宅被竊機率小於0.11
答案
(1) 過去遭竊率 = 0.6×0.15 + 0.4×0.05 = 0.09 + 0.02 = 0.11 = 11%，錯誤。
(2) 過去遭竊中A級占比 = 0.09 / 0.11 ≈ 81.8% \< 90%，錯誤。
(3) 改善後機率 0.03，原來 0.15，比值 0.03/0.15=1/5，正確。
(4) 改善後A級全體被竊率 = 0.2×0.03 + 0.8×0.15 = 0.006 + 0.12 = 0.126，B級 0.05，0.126 \gt 0.05，錯誤。
(5) 全體被竊率 = 0.6×0.126 + 0.4×0.05 = 0.0756 + 0.02 = 0.0956 \< 0.11，正確。
答案為 (3)(5)。
106指考數學乙試題-非選擇二(1)
袋中有紅色代幣4枚，綠色代幣9枚，以及藍色代幣若干枚。每一枚紅色、綠色、藍色代幣分別可兌換50元、20元及10元。現從袋中取出代幣，每一枚代幣被取出的機率均等。設隨機變數X代表取出1枚代幣可兌換的金額（單位：元）；隨機變數Y代表一次取出2枚代幣可兌換的金額（單位：元）。已知X的期望值為20。
(1)試問藍色代幣有多少枚？
答案
109指考數學乙(補考)試題-_B
坐標平面上有不共線的三點 \( A,B,C \) 且點 \( P \) 在線段 \( BC \) 上，並令 \( AP=xAB+yAC \)。若 \( BP=\frac{1}{2}CP \)，則 \( x \) 的值為 \(\underline{\quad }\)，\( y \) 的值為 \(\underline{\quad }\)。（化為最簡分數）
[選填題]
答案
109指考數學乙試題-_B
若隨機變數 \( X \) 的可能值為1、2、3、4，其出現的機率 \( P(X = k) \) 與 \( \frac{1}{k} \) 成正比，則機率 \( P(X = 3) \) 為 \( \boxed{9} \boxed{10} \)。（化為最簡分數）
[選填題]
答案
109指考數學乙試題-_C
一家公司僅有經理、秘書、業務三位成員，若只有秘書加薪10%，則全公司薪資總支出增加3%；若只有業務加薪20%，則全公司薪資總支出增加4%。如果只有經理減薪15%，那麼全公司薪資總支出將減少 \( \boxed{11} \boxed{12} \)。%
[選填題]
答案
設經理、秘書、業務薪資分別為\(a\)、\(b\)、\(c\)，全公司薪資總額\(T = a + b + c\)。
由條件：
- \(b \times 10\% = T \times 3\% \implies b = \frac{3}{10}T\)
- \(c \times 20\% = T \times 4\% \implies c = \frac{1}{5}T\)
因此經理薪資：
\[
a = T - \frac{3}{10}T - \frac{1}{5}T = \frac{1}{2}T
\]
若僅經理減薪15%，全公司薪資總支出減少比例為：
\[
\frac{\frac{1}{2}T \times 15\%}{T} = 7.5\%
\]
112學測數學B試題-01
某抽水站發現其用電量（單位：度）與抽水馬達轉速（單位：rpm）的三次方成正比。根據上述,試問下列這五個圖中,哪一個最可以描述此抽水站的用電量 \(y\)（度）與抽水馬達轉速 \(x\)（rpm）的對應關係？
答案
設 \(y = kx^{3}\)（\(k\gt0\)）,這是一個奇函數,當 \(x\gt0\) 時,函數單調遞增且為凸函數（\(y^\prime = 3kx^{2}\),\(y^{\prime\prime}=6kx\gt0\)）,從左到右上升趨勢越來越快。(1)
https://www.ceec.edu.tw/files/file_pool/1/0n045357541158913049/04-112%e5%ad%b8%e6%b8%ac%e6%95%b8%e5%ad%b8b%e9%81%b8%e6%93%87%28%e5%a1%ab%29%e9%a1%8c%e7%ad%94%e6%a1%88.pdf
111學測數學B試題-07
畫家把空間景物用單點透視法畫在平面的畫紙上時,有以下原則要遵守：一、空間中的直線畫在畫紙上必須是一條直線。二、空間直線上點的相關位置必須和畫紙所畫的點的相關位置一致。三、 空間 直 線上 的 任四個 相 異點的\(K\)值, 和畫 紙所畫 的四 個 點之\(K\)值 必 須相 同,其 中\(K\)值的定義如下：直線上任給四個有順序的相異點\(P_1\), \(P_2\), \(P_3\), \(P_4\) ,如下圖。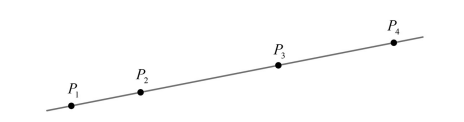
其所對應的\(K\)值定義為\[K=\frac{\overline{P_1P_4}\times \overline{P_2P_3}}{\overline{P_1P_3}\times \overline{P_2P_4}}\] 。今 某 畫家 依 照 以上 原 則, 將 空 間 中 一 直線 及 該 線 上的 四 相 異點\(Q_1\), \(Q_2\), \(Q_3\), \(Q_4\) 描 繪 在 畫 紙上,其中\(Q_1Q_2 = Q_2Q_3 = Q_3Q_4\) 。若將畫紙上所畫的直線視為一數線,並將線上的點用坐標來表示,則在下列選項的四個坐標中,試問哪一組最可能是該四點在畫紙上的坐標？
(1) \(1, 2, 4, 8\)；
(2) \(3, 4, 6, 9\)；
(3) \(1, 5, 8, 9\)；
(4) \(1, 2, 4, 9\)；
(5) \(1, 7, 9, 10\)
答案
$\begin{align*}
&定義交比K=\frac{3t×t}{2t×2t}=\frac{3}{4}，逐一計算選項：\\
&(1) K=\frac{7×2}{3×6}=\frac{7}{9}；\\
&(2) K=\frac{6×2}{3×5}=\frac{4}{5}；\\
&(3) K=\frac{8×3}{7×4}=\frac{6}{7}；\\
&(4) K=\frac{8×2}{3×7}=\frac{16}{21}；\\
&(5) K=\frac{9×2}{8×3}=\frac{3}{4}；\\
\\
&故選(5)。
\end{align*}$
https://www.ceec.edu.tw/files/file_pool/1/0m053363176747148935/04-111%e5%ad%b8%e6%b8%ac%e6%95%b8%e5%ad%b8b%e9%81%b8%e6%93%87%28%e5%a1%ab%29%e9%a1%8c%e7%ad%94%e6%a1%88.pdf