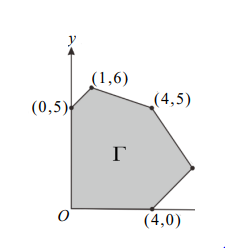
二、(2) 試在坐標平面上,畫出滿足題幹條件 \((x,y)\) 的可行解區域,並以斜線標示該區域。
[非選擇題]線性規劃
110指考數學乙試題-非選擇二(3)
二、(3) 試求當倍數 \(x,y\) 分別為多少時,甲、乙兩型電動車的售價差距最大?此時甲、乙兩型電動車的售價差距為多少萬元?
[非選擇題]$\begin{align*}
&(3) 目標函數(甲、乙售價差距):\\
&(80x + 50y) - (68x + 48y) = 12x + 2y。\\
\\
&頂點法計算:\\
&\begin{array}{|c|c|c|c|c|}
\hline
(x,y) & (1,1) & \left(\frac{15}{8},1\right) & \left(\frac{5}{4},2\right) & (1,2) \\
\hline
12x + 2y & 14 & 24.5 & 19 & 16 \\
\hline
\end{array}\\
\\
&故當x=\frac{15}{8},\ y=1時,售價差距最大值為24.5萬元。
\end{align*}$
109指考數學乙(補考)試題-04
坐標平面上,設 \( a, b \) 為實數,已知目標函數 \( ax + by \) 在平面區域 \(\Omega\):\(\begin{cases} 4x + y \leq 16 \\ -2x + 3y \leq 6 \\ x \geq 0 \\ y \geq 0 \end{cases}\)的最大值為12,且取得最大值的點不在坐標軸上。試選出正確的選項。
(1) \( 4a + 3b = 12 \)
(2) \( -\frac{a}{b} > -3 \)
(3) \( -\frac{a}{b} < \frac{2}{3} \)
(4) \( b \)可能為\(-3\)
(5) \( b \)可能為\( 1 \)
\begin{align*}
&\boxed{【頂點法】} \\
&因為最大值必發生在頂點,我們將可行解區的頂點代入目標函數: \\
\\
&\begin{array}{|c|c|c|c|c|}
\hline
(x, y) & (0, 2) & (3, 4) & (4, 0) & (0, 0) \\
\hline
ax + by & 2b & 3a + 4b & 4a & 0 \\
\hline
\end{array} \\
\\
&依題意,取得最大值的點為(3,4),故 \ 3a + 4b = 12 \,且: \\
&\begin{cases}
3a + 4b = 12 > 2b \\
3a + 4b = 12 > 4a \\
3a + 4b = 12 > 0
\end{cases} \implies \begin{cases}
b < 6 \\
a < 3
\end{cases} \\
\\
&我們都可以將 \ a \ 用 \ 3a + 4b = 12 \ 代換:\ a = 4 - \frac{4b}{3},故: \\
&a < 3 \implies 4 - \frac{4b}{3} < 3 \implies b > \frac{3}{4} \\
\\
&(1) \ 由上知 \ 3a + 4b = 12 \ ; \\
\\
&(2)(3)(4)(5): \\
&-\frac{a}{b} = -\frac{4 - \frac{4b}{3}}{b} = -\frac{4}{b} + \frac{4}{3},而 \ \frac{3}{4} < b < 6,所以: \\
&-\frac{16}{3} < -\frac{4}{b} < -\frac{2}{3} \implies -4 < -\frac{4}{b} + \frac{4}{3} < \frac{2}{3},故 \ -4 < -\frac{a}{b} < \frac{2}{3},因此(2)錯誤,(3)正確; \\
\\
&並得到 \ \frac{3}{4} < b < 6,所以(4)錯誤,(5)正確。
\end{align*}
109指考數學乙試題-_A
108指考數學乙試題-非選擇二(1)
某運輸公司欲向一汽機車製造商訂購一批重型機車(簡稱重機)和汽車。其訂購費用為重機一部25萬元及汽車一部60萬元,訂購經費上限是5400萬元。另此運輸公司共有100格停車位,每格停車位恰可停放兩部重機或是停放一部汽車。而此運輸公司每銷售1部重機可得淨利潤2.3萬元(即2萬3千元),銷售1部汽車則可得淨利潤5萬元,並假設此運輸公司可將其所訂購之重機及汽車全數銷售完畢。此運輸公司希望能在訂購經費的上限和停車位之限制下獲得最大的淨利潤。試回答下列問題。
(1) 試寫出此問題之線性規劃不等式及目標函數。
108指考數學乙試題-非選擇二(2)
(2) 在坐標平面上畫出可行解區域,並以斜線標示該區域。
[非選擇題]約束條件:
1. \(25x + 60y \leq 5400\) → \(5x + 12y \leq 1080\)
2. \(\frac{x}{2} + y \leq 100\) → \(x + 2y \leq 200\)
3. \(x \geq 0, y \geq 0\)
交點:
- \(x+2y=200\) 與 \(5x+12y=1080\) 解聯立:\(5(200-2y)+12y=1080\) → \(1000-10y+12y=1080\) → \(2y=80\) → \(y=40\), \(x=120\)
- \(x+2y=200\) 與 \(x=0\):\(y=100\)
- \(5x+12y=1080\) 與 \(y=0\):\(x=216\)
可行解區域為四邊形頂點 \((0,0)\), \((0,90)\), \((120,40)\), \((200,0)\) 的凸多邊形區域。
108指考數學乙試題-非選擇二(3)
(3) 此運輸公司應訂購重機、汽車各多少部才能獲得最大的淨利潤?此最大淨利潤為何?
[非選擇題]114分科測驗數學乙考科試卷-17(非選擇二)
[16-18為題組]承16題,將三個條件以二元一次聯立不等式表示。
17. 試將某人對甲面積、乙面積所設定的三個條件,以 \(x\)、\(y\) 的二元一次聯立不等式表示。(非選擇題,4 分)
114分科測驗數學乙考科試卷-18(非選擇二)
[16-18為題組]18. 已知某人的農地收成時,甲水果每公畝可獲利 6 萬元、乙水果每公畝可獲利 7 萬元。
試 求 某 人 種 植 甲 、 乙 兩 種 水 果 的 最 大 獲 利 為 多 少 萬 元 ? 在 答 題 卷 求 解 區 寫 出計 算 過 程,並 在 答 題 卷 作 圖 區 畫 出 可 行 解 區 域 及 標 出 其 所 有 頂 點 坐 標,且 以 斜 線標 示 該 區 域 。( 非 選 擇 題 , 8 分 )
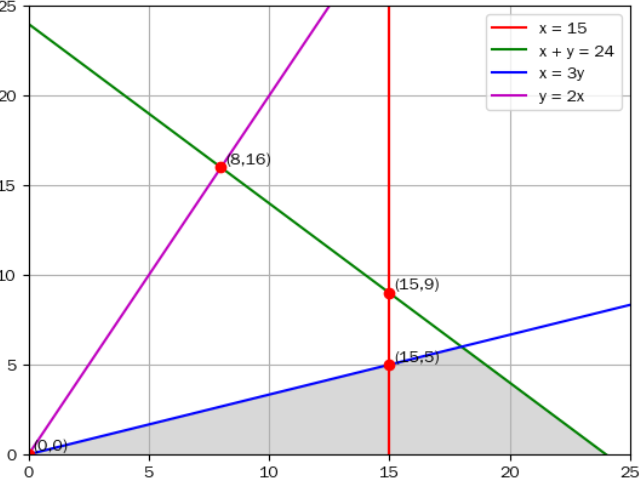
好的,我們先列出所有條件,再用線性規劃求解。
---
## **1. 列出限制條件**
題目給定:
1. \( x \le 15 \)
2. \( x + y \le 24 \)
3. \( x \le 3y \) 且 \( y \le 2x \)
4. \( x \ge 0, \quad y \ge 0 \) (面積不能為負)
---
## **2. 化簡條件 3**
條件 3 拆開:
\[
x \le 3y \quad \Rightarrow \quad y \ge \frac{x}{3}
\]
\[
y \le 2x
\]
所以:
\[
\frac{x}{3} \le y \le 2x
\]
---
## **3. 聯立所有條件**
我們有:
\[
\begin{cases}
0 \le x \le 15 \\
x + y \le 24 \\
y \ge \frac{x}{3} \\
y \le 2x
\end{cases}
\]
---
## **4. 找可行解區域的頂點**
**(1) 交點 \(x=15\) 與 \(x+y=24\)**
\(y = 9\)
檢查 \(y \ge \frac{15}{3} = 5\) ✅
檢查 \(y \le 2\times 15 = 30\) ✅
⇒ 頂點 \(A = (15, 9)\)
**(2) 交點 \(x=15\) 與 \(y=2x\)**
\(y = 30\),但 \(x+y = 45 > 24\) 不行,所以此點不在 \(x+y \le 24\) 內,不考慮。
**(3) 交點 \(x+y=24\) 與 \(y=2x\)**
代入:\(x + 2x = 24 \Rightarrow 3x = 24 \Rightarrow x=8, y=16\)
檢查 \(x \le 15\) ✅
檢查 \(y \ge \frac{8}{3} \approx 2.67\) ✅
⇒ 頂點 \(B = (8, 16)\)
**(4) 交點 \(x+y=24\) 與 \(y = \frac{x}{3}\)**
代入:\(x + \frac{x}{3} = 24 \Rightarrow \frac{4x}{3} = 24 \Rightarrow x = 18\)
但 \(x=18 > 15\),所以此交點不在 \(x \le 15\) 內,不考慮。
**(5) 交點 \(x=15\) 與 \(y = \frac{x}{3}\)**
\(y = 5\),檢查 \(x+y = 20 \le 24\) ✅
⇒ 頂點 \(C = (15, 5)\)
**(6) 交點 \(y = \frac{x}{3}\) 與 \(y = 2x\)**
只有 \(x=0, y=0\),但那是原點 \(O=(0,0)\)。
**(7) 交點 \(y=2x\) 與 \(x=0\)**
\( (0,0) \) 重複。
**(8) 交點 \(x=0\) 與 \(y=0\)** 原點。
但原點利潤最低,顯然不是最大。
---
我們還要檢查 \(x+y=24\) 與 \(x=15\) 之間是否還有其他頂點受 \(y \ge x/3\) 與 \(y \le 2x\) 限制。
實際上,在 \(x=15\) 時,\(y\) 範圍是 \(5 \le y \le 9\)(因為 \(x+y \le 24 \Rightarrow y \le 9\),且 \(y \ge 5\) 來自 \(y \ge x/3\))。
所以 \(x=15\) 邊上兩個端點:\((15,5)\) 和 \((15,9)\) 已取。
在 \(x<15\) 時,最大 \(y\) 受 \(x+y=24\) 與 \(y \le 2x\) 限制,交點是 \(B=(8,16)\)。 檢查 \(y \ge x/3\):\(16 \ge 8/3\) ✅。 --- 所以主要頂點為: \[ O=(0,0), \quad C=(15,5), \quad A=(15,9), \quad B=(8,16) \] --- ## **5. 目標函數** 利潤: \[ P = 6x + 7y \ (\text{萬元}) \] 代入: - \(O\): \(P=0\) - \(C=(15,5)\): \(P=6\times 15 + 7\times 5 = 90+35=125\) - \(A=(15,9)\): \(P=90+63=153\) - \(B=(8,16)\): \(P=48+112=160\) 最大利潤在 \(B=(8,16)\),\(P=160\) 萬元。 --- ## **6. 檢查是否還有更大點** 在 \(x+y=24\) 上,\(y=24-x\), \(P=6x+7(24-x) = 168 - x\),隨 \(x\) 減小而增大,但必須滿足 \(y \le 2x \Rightarrow 24-x \le 2x \Rightarrow 24 \le 3x \Rightarrow x \ge 8\), 且 \(y \ge x/3 \Rightarrow 24-x \ge x/3 \Rightarrow 72-3x \ge x \Rightarrow 72 \ge 4x \Rightarrow x \le 18\)(但 \(x \le 15\) 更嚴格)。 所以 \(x\) 範圍 \(8 \le x \le 15\) 在 \(x+y=24\) 上。 \(P=168-x\) 在 \(x=8\) 最大 \(160\),在 \(x=15\) 時 \(153\)。 所以 \(B\) 點確實最大。 --- **最終答案:** \[ \boxed{160} \] 最大利潤 160 萬元,此時 \(x=8\) 公畝,\(y=16\) 公畝。
106指考數學甲試題–C
坐標平面上,\(x\)坐標與\(y\)坐標均為整數的點稱為格子點。令\(n\)為正整數,\(T_n\)為平面上以直線\(y=\frac{-1}{2n}x + 3\),以及\(x\)軸、\(y\)軸所圍成的三角形區域(包含邊界),而\(a_n\)為\(T_n\)上的格子點數目,則\(\lim_{n \to \infty}\frac{a_n}{n}=\)____。
[選填題]設 \( A(6n, 0) \)、\( B(0, 3) \),直線 \( AB \) 的方程為 \( y = -\frac{1}{2n}x + 3 \),\( T_n \) 是 \( \triangle OAB \) 內部(含邊界)的區域。
統計 \( T_n \) 內整數點的個數 \( a_n \):
- 當 \( y=0 \) 時,\( x \) 可取 \( 0 \sim 6n \),共 \( 6n+1 \) 個點;
- 當 \( y=1 \) 時,代入直線方程得 \( x \leq 4n \),故 \( x \) 可取 \( 0 \sim 4n \),共 \( 4n+1 \) 個點;
- 當 \( y=2 \) 時,代入得 \( x \leq 2n \),故 \( x \) 可取 \( 0 \sim 2n \),共 \( 2n+1 \) 個點;
- 當 \( y=3 \) 時,僅有 \( (0, 3) \),共 \( 1 \) 個點。
因此:
\[
a_n = (6n+1) + (4n+1) + (2n+1) + 1 = 12n + 4
\]
求極限:
\[
\lim_{n \to \infty} \frac{a_n}{n} = \lim_{n \to \infty} \frac{12n + 4}{n} = 12
\]